この記事は『CRESCO Advent Calendar 2021』の18日目の記事です。
みなさんこんにちは。データテクノロジーセンターの飯村北海です。
昨年度からできた部門で引き続き、[PR]Tableauなどを活用したBI導入サービスを提供しています。
もうすぐ2021年も終わりますね(昨年も書いた気がする…)。アドベントカレンダーのシーズンです。今年はあっという間の2021年でした。IT業界の皆様は今年も引き続き、リモートワークをされていた皆様が多かったのではないでしょうか?
私は数年ぶりに引っ越しをしました。第2子が生まれたことで住んでいた家が手狭になったことや、リモートワークがなかなか難しい環境だったこともあり、本格的なリモートワークに向けて引っ越しをしました。今は環境も整いそれなりに快適に仕事ができるようになりました。しかし、これから本格的にテレワークを始めるぞ!というのは今更かもしれません…
さて、今日の記事はデータ可視化に重要なデータ構造の話を取り上げたいと思います。
この前、Tableauのダッシュボードを作る時にとある人から「どういうデータでTableauのダッシュボードを作ればよいのかわかりにくい」という相談を受けました。エクセルでグラフを作るときは手元でデータを加工しながらつくりますが、Tableau Desktop (や、Server/OnlineのWeb編集自体の機能)ではその場でデータ構造を大きく変えることはできません。
データ加工をしたい場合はTableau Desktopが参照するデータに対して別なツールを用意して加工します。Tableau社でもTableau Prep Builderと呼ばれるPCで動作可能なGUIのツールを提供しており、それを使えば(機能上の制約や限界はありますが)加工が可能です。事前に使用するデータ構造を意識できると、自分が表現したいダッシュボードを作りやすくなります。
また、とあるTableauのダッシュボード作成プロジェクトに参画したのですが、そこで定義されているDBのテーブル定義ではTableauでやりたいことができなかったのでデータ加工が大変だった、という話も聞きました。
そこでTableau に不慣れな人が「どういうデータ構造でどういうチャートを作らないといけないかがイメージしにくい」のでその課題を解決するべく、イメージを持ってもらえるようにサンプルを代表的なデータ構造とともに提示したいと思ったのが今回のテーマの発端です。
データ構造に言及した記事は過去にも他の社員や私がエンジニアブログで書いています。
ここではもう少し掘り下げて見ていきたいと思います。
※以降で取り扱うデータ構造は行と列で表現ができる構造(key-valueなどではなく、データフレーム)を前提とします。
JSONやリストや音声、画像データなどの非構造化データは対象としません。
いわゆる縦持ち・横持ちデータと呼ばれるデータはなんなのか?ということを考えてみたいと思います。
今回、縦持ち・横持ちのデータ構造の記事を書くにあたりいろいろと調べてみましたが、なかなか定義が難しく、結論から言うと、処理上で縦に長くなるデータ、横に長くなるデータとしか言いようがないなぁということになりました。
もう少し補足すると、データを新規に追加する意図がある場合にその方向が縦であれば縦持ちデータ、横方向なら横持ちデータと言えるのではないでしょうか。
縦持ちデータ・横持ちデータそれぞれについて簡単にまとめてみました。これはデータベースで設計される時の構造も含んでいます。
表1. 縦持ち、横持ちデータの特徴
| 縦持ち | 横持ち | |
| 別名 |
|
|
| メリット |
|
|
| デメリット |
|
|
※ tidy dataについては後述します
横持ちデータを下記の具体的なサンプルデータで確認してみます。
表2. 年月が横に並ぶデータ1
| 値 | 2021年1月 | 2021年2月 | 2021年3月 | 2021年4月 | 2021年5月 | 2021年6月 | 2021年7月 | 2021年8月 | 2021年9月 | 2021年10月 | 2021年11月 | 2021年12月 |
| 売上 | \3,542,034 | \3,347,115 | \3,615,664 | \4,047,938 | \7,598,055 | \7,467,338 | \4,231,340 | \8,752,818 | \8,881,966 | \7,377,961 | \5,912,118 | \8,110,618 |
| 利益 | \304,685 | \444,982 | \256,616 | \402,444 | \862,787 | \543,601 | \543,822 | \1,123,394 | \1,316,052 | \860,584 | \723,871 | \900,303 |
| 利益率 | 9% | 13% | 7% | 10% | 11% | 7% | 13% | 13% | 15% | 12% | 12% | 11% |
※Tableauのサンプルスーパーストアより加工
こちらのデータは横に年月が伸びていくデータです(2021年の1月から12カ月分あります)、数値が含まれているものは3行12列、36セルあります。1行目が売上、2行目が利益、3行目が利益率となっています(Wordpressの幅の都合上、右側が切れています。スミマセン)。
販売数量や原価、といった項目を縦に伸ばすというよりは年月で3つの値を横に増やしていく特性が強いデータ構造になっていると思います。
※なので、次にデータが増えるなら2022年1月の売上、利益、利益率が追加されることになるでしょう。
表3. 年月が横に並ぶデータ2
| 四半期 | アプライアンス | クリップ | コピー機 | テーブル | バインダー | ラベル | 椅子 | 家具 | 画材 | 紙 | 事務機器 | 電話機 | 付属品 | 封筒 | 文房具 | 保管箱 | 本棚 |
| Q1 | ¥3,877,623 | ¥332,895 | ¥4,530,953 | ¥2,672,609 | ¥693,699 | ¥189,864 | ¥4,250,769 | ¥1,170,516 | ¥561,155 | ¥558,421 | ¥1,431,138 | ¥3,391,758 | ¥2,544,408 | ¥524,890 | ¥639,023 | ¥2,158,701 | ¥4,011,243 |
| Q2 | ¥7,919,647 | ¥520,743 | ¥7,994,291 | ¥4,726,587 | ¥1,047,235 | ¥362,231 | ¥8,893,459 | ¥1,834,341 | ¥968,847 | ¥1,072,964 | ¥3,354,356 | ¥8,225,214 | ¥3,900,865 | ¥971,897 | ¥1,136,062 | ¥3,180,635 | ¥7,661,802 |
| Q3 | ¥7,972,016 | ¥426,229 | ¥7,863,602 | ¥4,052,743 | ¥1,101,316 | ¥325,053 | ¥8,451,937 | ¥1,724,215 | ¥1,137,757 | ¥961,354 | ¥3,064,904 | ¥6,773,180 | ¥3,530,988 | ¥877,118 | ¥948,633 | ¥3,619,658 | ¥8,428,277 |
| Q4 | ¥8,186,900 | ¥608,978 | ¥9,343,063 | ¥2,467,847 | ¥1,286,095 | ¥401,418 | ¥9,762,111 | ¥2,025,182 | ¥1,174,321 | ¥1,127,708 | ¥3,152,517 | ¥9,325,858 | ¥3,860,461 | ¥1,066,761 | ¥1,541,047 | ¥4,243,396 | ¥9,033,362 |
※Tableauのサンプルスーパーストアより加工
こちらのデータは横にサブカテゴリを並べているデータです、数値が含まれているものは4行17列、68セルあります。1行目から下に四半期ごとの売上となっています(こちらも右側が切れています)。こちらも四半期なのでどちらかと言えばサブカテゴリが増えればその項目ごとに売り上げを横に伸ばしていくことになるデータと言えるでしょう。
表4. 試験を実施して横に受験者が並ぶデータ
| 科目 | 甲坂 子朗生 | 乙飼 丑明羅 | 丙野 寅雪貴 | 丁木 卯心 | 戊部 辰市 | |
| 国語 | 54 | 74 | 77 | 95 | 82 | … |
| 数学 | 71 | 66 | 65 | 65 | 96 | … |
| 理科 | 62 | 75 | 66 | 55 | 74 | … |
| 社会 | 65 | 66 | 62 | 63 | 68 | … |
| 英語 | 67 | 79 | 82 | 100 | 86 | … |
※独自に作成
こちらのデータは5名の受験者が国語数学理科社会英語の5教科を受験した結果の得点データです。数値が含まれているものは5列5行、25セルあります。主要5教科に対して、受験者が6名いることになりますが、こちらも同様にデータの増え方としては6人目、7人目と横に伸びて表示されることになるデータとなるでしょう。
これらの横持ちデータを実際にご覧になってどのように感じるでしょうか?メリットにも書いたようにデータが理解しやすい構造になっていると思います。(量にもよりますが)そのままエクセルに貼り付けて報告もできそうです。
一方で、例えば年月のデータセットを取り上げた時に、エクセルなどで列の合計を算出した後で、新しく一番右側の列にデータを追加した場合は項目数が追加されるので(SUM関数などで範囲を指定した場合は合計の範囲が変える必要があるので)都度手直しをする必要があるかもしれません。
縦持ちデータの説明をする前に、クロス表のデータについて取り上げます。
横持ちデータに少し似ていますが、クロス表は横持ちデータの構造とはまた別なのではないかと思い、別の種類としてセクションを分けました。下記の2種類のデータを見てみましょう。
表5. 曜日が横に並ぶデータ
| 週数 | 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| 週 15 | なし | 可燃 | なし | 資源 | 可燃 | なし | プラ |
| 週 16 | なし | 可燃 | なし | 資源 | 可燃 | 不燃 | プラ |
| 週 17 | なし | 可燃 | なし | 資源 | 可燃 | なし | プラ |
| 週 18 | なし | 可燃 | なし | 資源 | 可燃 | なし | プラ |
| 週 19 | なし | 可燃 | なし | 資源 | 可燃 | 不燃 | プラ |
| 週 20 | なし | 可燃 | なし | 資源 | 可燃 | なし | プラ |
| 週 21 | なし | 可燃 | なし | 資源 | 可燃 | 不燃 | プラ |
| 週 22 | なし | 可燃 | なし | 資源 | 可燃 | なし | プラ |
| 週 23 | なし | 可燃 | なし | 資源 | 可燃 | 不燃 | プラ |
| 週 24 | なし | 可燃 | なし | 資源 | 可燃 | なし | プラ |
| 週 25 | なし | 可燃 | なし | 資源 | 可燃 | 不燃 | プラ |
| … | … | … | … | … | … | … |
※港区のゴミ収集カレンダーより作成(港南1〜5丁目エリア)
こちらは横に曜日、縦に週数(週2の月が2021年1月2日)で表示されたデータです。7列11行77セルあります。こちらは数値ではなく、属性が入っています。
表6. 地方が横に並び、期間が縦に並ぶデータ
| 四半期 | 北海道 | 東北地方 | 中部地方 | 関東地方 | 関西地方 | 中国地方 | 四国 | 九州 |
| Q1 | \614,640 | \2,575,074 | \7,648,829 | \5,534,517 | \8,197,173 | \3,448,550 | \1,217,789 | \4,303,093 |
| Q2 | \1,286,546 | \3,858,765 | \12,157,281 | \13,572,157 | \16,892,735 | \5,546,177 | \2,789,491 | \7,668,022 |
| Q3 | \1,186,919 | \4,920,664 | \10,642,581 | \15,137,583 | \14,288,436 | \4,804,752 | \2,603,717 | \7,674,326 |
| Q4 | \1,559,082 | \5,628,009 | \12,449,844 | \14,278,805 | \17,522,957 | \5,670,284 | \3,162,961 | \8,335,081 |
こちらは横に地方、縦に四半期で集計されたデータです。数値が含まれているものは8列4行32セルあります。
一見、縦や横にデータが増やせそうで、それぞれ縦持ちデータ、横持ちデータと呼べそうです。しかし、列や行の項目をよく見てみると「週数」や「曜日」の列、「四半期」の値はそれぞれ1週〜52週(もしくは53週)、日〜土、1Q〜4Qと繰り返す項目であったり、「地方」の列はリストで事前に定義可能な有限の項目です。なのでデータを追加していくというよりはその項目で完成されたデータという特性で縦持ちデータ、横持ちデータと別の役割を持つのではないかと思います。クロス表データが作成される背景としては行や列の項目の観点で値を集計する目的が多く「クロス集計表」と呼ばれる方が多いのですがこの記事ではクロス表データと呼びます。
横持ちデータもクロス表データも、人が見て全体がわかりやすいことが特徴です。また、横持ちと同様に保持しているデータそのままで使う(印刷など)ことができること、(数値であれば)列同士を加算すれば合計を作成できる構造になっています。
一方で縦持ちデータの例ですが、前述してきた横持ちデータを縦持ちデータにした場合は下記となります。
※最初の10行のみ表示しています。
表6.「年月が横に並ぶデータ1」を縦持ちにしたデータ
| オーダー年月 | 売上 | 利益率 | 利益 |
| 2021年1月 | \3,542,034 | 9% | \304,685 |
| 2021年2月 | \3,347,115 | 13% | \444,982 |
| 2021年3月 | \3,615,664 | 7% | \256,616 |
| 2021年4月 | \4,047,938 | 10% | \402,444 |
| 2021年5月 | \7,598,055 | 11% | \862,787 |
| 2021年6月 | \7,467,338 | 7% | \543,601 |
| 2021年7月 | \4,231,340 | 13% | \543,822 |
| 2021年8月 | \8,752,818 | 13% | \1,123,394 |
| 2021年9月 | \8,881,966 | 15% | \1,316,052 |
| 2021年10月 | \7,377,961 | 12% | \860,584 |
| … | … | … |
表7. 「年月が横に並ぶデータ2」を縦持ちにしたデータ
| 四半期 | サブカテゴリ | 売上 |
| Q1 | アプライアンス | \3,877,623 |
| Q2 | アプライアンス | \7,919,647 |
| Q3 | アプライアンス | \7,972,016 |
| Q4 | アプライアンス | \8,186,900 |
| Q1 | クリップ | \332,895 |
| Q2 | クリップ | \520,743 |
| Q3 | クリップ | \426,229 |
| Q4 | クリップ | \608,978 |
| Q1 | コピー機 | \4,530,953 |
| Q2 | コピー機 | \7,994,291 |
| … |
表7. 「試験を実施して横に受験者が並ぶデータ」を縦持ちにしたデータ
| 受験者名 | 科目 | 得点 |
| 乙飼 丑明羅 | 英語 | 69 |
| 乙飼 丑明羅 | 国語 | 75 |
| 乙飼 丑明羅 | 社会 | 77 |
| 乙飼 丑明羅 | 数学 | 87 |
| 乙飼 丑明羅 | 理科 | 56 |
| 己田 巳規雄 | 英語 | 52 |
| 己田 巳規雄 | 国語 | 89 |
| 己田 巳規雄 | 社会 | 68 |
| 己田 巳規雄 | 数学 | 64 |
| 己田 巳規雄 | 理科 | 78 |
| … |
表8. 「曜日が横に並ぶデータ」を縦持ちにしたデータ
|
週数
|
曜日
|
収集種別
|
|
週14
|
木
|
可燃
|
|
週14
|
金
|
不燃
|
|
週14
|
土
|
プラ
|
|
週15
|
日
|
なし
|
|
週15
|
月
|
可燃
|
|
週15
|
火
|
なし
|
|
週15
|
水
|
資源
|
|
週15
|
木
|
可燃
|
|
週15
|
金
|
なし
|
|
週15
|
土
|
プラ
|
| … |
これらの縦に長いデータは途中で省略していますが、かなり縦に長くなっていくため、視認性が下がります。しかし、例えば表7を例にすると、音楽や美術など新しい科目を新たに追加したい場合には、行を追加するだけなので簡単にデータを(定義として)追加することができます。
一方で横持ちデータの場合(表4)は列として一番右側に追加する必要があるため、表1の特徴で説明したように行単位で加算する計算はしやすいものの、列が追加されるたびに加算対象の列に追加される列を加える修正をしなければなりません(縦持ちデータの場合は不要です)。
1番目のサンプルで先月との差分(先月比)を出したい、という時には横持ちデータの方が計算はしやすいでしょう。
データ分析(データサイエンス分野)をする上で言及しておくべきデータ構造があります。Tidy data(日本では整然データと呼ばれることが多い)と呼ばれるものです。
この概念は2014年にニュージーランド出身のHadley Wickham(ハドリー・ウィッカム)によって提唱されました。
初出の論文はこちらのリンクから読むことができます。同様の文章はこちらのリンクからも確認ができます(いずれも英語)。
こちらの定義によれば、Tidyなデータとは下記を満たすものです。
- Every column is a variable. (各列は一つの変数を表す)
- Every row is an observation. (各行は一組の観測値を表す)
- Every cell is a single value. (各セルは一つの値を表す)
とあります。Tidy data自体の解説は色々な方々がされているのでここであまり詳しくは書きませんが、説明したいと思います。
ここで下記のようなデータ構造を見てみましょう。先ほどのゴミ収集カレンダーに手を加えたものです。月曜日に粗大ゴミを追加したデータです。
表9. ゴミ収集カレンダーに粗大ゴミを追加したデータ
| 週数 | 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| 第1週 | なし | 可燃 粗大 |
なし | 資源 | 可燃 | なし | プラ |
| 第2週 | なし | 可燃 粗大 |
なし | 資源 | 可燃 | 不燃 | プラ |
| 第3週 | なし | 可燃 粗大 |
なし | 資源 | 可燃 | なし | プラ |
| 第4週 | なし | 可燃 粗大 |
なし | 資源 | 可燃 | 不燃 | プラ |
ここで、1つ目の定義である「Every column is a variable.」を取り上げます。各列は曜日となっていますが、よく考えてみればこのデータは各日付に対して収集するゴミの種類を記載しているもので、曜日で横に並べているのは人が見てわかりやすくしているだけに過ぎません。各日に対して、何を収集するかが記載されていれば良いので次のようになるでしょう(第2週までにデータを減らしました)。
表10. 週数、曜日、種類に変更したゴミ収集カレンダーデータ
| 週数 | 曜日 | 種類 |
| 第1週 | 日 | なし |
| 第1週 | 月 | 可燃 粗大 |
| 第1週 | 火 | なし |
| 第1週 | 水 | 資源 |
| 第1週 | 木 | 可燃 |
| 第1週 | 金 | なし |
| 第1週 | 土 | プラ |
| 第2週 | 日 | なし |
| 第2週 | 月 | 可燃 粗大 |
| 第2週 | 火 | なし |
| 第2週 | 水 | 資源 |
| 第2週 | 木 | 可燃 |
| 第2週 | 金 | 船 |
| 第2週 | 土 | プラ |
これで1番目の定義「Every column is a variable.」を満たすことができます。ちなみに表9の状態では「Every row is an observatrion.」という定義も満たしていませんでした。1行取り上げた時に日〜土で7つのデータが観測されてしまうことになります。これでは2番目の定義は満たせません。縦に並べることで1行(1つの観測)で1つの日付のデータが表現されるようになっています。
次に、月曜日を取り上げます。これは1つのセルに可燃ゴミと粗大ゴミの2つの値(属性)が入っていることになるため、3番目の定義である「Every cell is a single value」を満たしていません。3番目の定義も満たすようにデータを変えると下記のようになります(赤字が変更箇所)。
表11. 3つの定義を満たしたデータ
| 週数 | 曜日 | 種類 |
| 第1週 | 日 | なし |
| 第1週 | 月 | 可燃 |
| 第1週 | 月 | 粗大 |
| 第1週 | 火 | なし |
| 第1週 | 水 | 資源 |
| 第1週 | 木 | 可燃 |
| 第1週 | 金 | なし |
| 第1週 | 土 | プラ |
| 第2週 | 日 | なし |
| 第2週 | 月 | 可燃 |
| 第2週 | 月 | 粗大 |
| 第2週 | 火 | なし |
| 第2週 | 水 | 資源 |
| 第2週 | 木 | 可燃 |
| 第2週 | 金 | 船 |
| 第2週 | 土 | プラ |
値の変更はされていますが、行数でいうと、月曜日の行が2行増えたことになります。
上記の状態がtidyなデータと言えます。
※このデータの例では種類が唯一の値の列として作成されていますが、観測時の観点(意図)によっては後述(表12)のような2種類の値の状態でtidyなデータとすることもあるようです。詳しくは前述の論文を参照して下さい。
さて、一通りデータ構造の説明をしたところで、実際にTableauでどのようなグラフが作成できるか見ていきましょう。データ構造が変わると作成できるTableauのグラフが変わっていくはずです。もちろん、工夫すれば同じように作れるものもありますが、少しづつ変わっていく差を見ていきましょう。
用意したデータは下記のディメンションとメジャーを含むデータで作っていきます。Tableauに付属しているスーパーストアから作成しています。データ構造によって列名が変更されていることがありますが、基本的には値は必ず網羅されています。
- オーダー年月(2021年1月〜2021年12月)
- 顧客区分(大企業/小規模事業所/消費者)
- 区分(売上/利益)
- 売上
- 利益
用意したデータセットは下記の通りです。データを見てみればどういう構造になっているかわかると思います。
- 縦持ちデータ1
- 縦持ちデータ2
- 横持ちデータ1
- クロス表データ1
- クロス表データ2
表12. 縦持ちデータ1(抜粋)
| オーダー年月 | 顧客区分 | 利益 | 売上 |
| 2021年1月 | 小規模事業所 | 147936 | 790700 |
| 2021年1月 | 消費者 | 212045 | 2012131 |
| 2021年1月 | 大企業 | -55296 | 739203 |
| 2021年2月 | 小規模事業所 | 122171 | 1053810 |
| 2021年2月 | 消費者 | 309234 | 1317668 |
| 2021年2月 | 大企業 | 13578 | 975638 |
| … | |||
表13. 縦持ちデータ2(抜粋)
| 区分 | オーダー年月 | 顧客区分 | 値 |
| 利益 | 2021年1月 | 小規模事業所 | 147936 |
| 売上 | 2021年1月 | 小規模事業所 | 790700 |
| 利益 | 2021年1月 | 消費者 | 212045 |
| 売上 | 2021年1月 | 消費者 | 2012131 |
| 利益 | 2021年1月 | 大企業 | -55296 |
| 売上 | 2021年1月 | 大企業 | 739203 |
| 利益 | 2021年2月 | 小規模事業所 | 122171 |
| 売上 | 2021年2月 | 小規模事業所 | 1053810 |
| 利益 | 2021年2月 | 消費者 | 309234 |
| 売上 | 2021年2月 | 消費者 | 1317668 |
| 利益 | 2021年2月 | 大企業 | 13578 |
| 売上 | 2021年2月 | 大企業 | 975638 |
| … |
表14. 横持ちデータ(抜粋)
| 区分 | 顧客区分 | 2021年1月 | 2021年2月 | |
| 利益 | 小規模事業所 | 147936 | 122171 | … |
| 利益 | 消費者 | 212045 | 309234 | |
| 利益 | 大企業 | -55296 | 13578 | |
| 売上 | 小規模事業所 | 790700 | 1053810 | |
| 売上 | 消費者 | 2012131 | 1317668 | |
| 売上 | 大企業 | 739203 | 975638 |
表15. クロス表データ1(抜粋)
| 売上 | 売上 | 売上 | 利益 | 利益 | 利益 | |
| オーダー年月 | 小規模事業所 | 消費者 | 大企業 | 小規模事業所 | 消費者 | 大企業 |
| 2021年1月 | 790700 | 2012131 | 739203 | 147936 | 212045 | -55296 |
| 2021年2月 | 1053810 | 1317668 | 975638 | 122171 | 309234 | 13578 |
| … | ||||||
表16. クロス表データ2(抜粋)
| 区分 | オーダー年月 | 小規模事業所 | 消費者 | 大企業 |
| 売上 | 2021年1月 | 790700 | 2012131 | 739203 |
| 利益 | 2021年1月 | 147936 | 212045 | -55296 |
| 売上 | 2021年2月 | 1053810 | 1317668 | 975638 |
| 利益 | 2021年2月 | 122171 | 309234 | 13578 |
| … | ||||
作成するグラフは下記の通りです。大体Tableauで作成する主要なものを挙げてみました。
- 数表
- 折れ線グラフ
- 帯グラフ
- 棒と線の複合グラフ
- 円グラフ
- ツリーマップ
下記のルールでグラフを作っていくことにします。下記にないものはいい感じに。ということで…
- よく使いそうなグラフ表現を作成する
- できる限りマークを使用してわかりやすい表現でグラフを作成する
- Tableau Desktop上でピボットはしない(データ構造の前提が変わってしまうので)
- 計算フィールドは作っても良い
- できる限り書式はそのまま(一部見やすくしたり、試行錯誤の中で色が変化した場合は変更しています)
- 作れなかったら作れるところまで頑張る
まずは一番簡単な数表を作成してみたいと思います。数表は一見簡単に見えるのですが、可視化をするのが得意なTableauは数表を作るのが実は苦手だったりします。もちろん今回は昨対比などの計算をしないものなので、そこまで難しくありません。
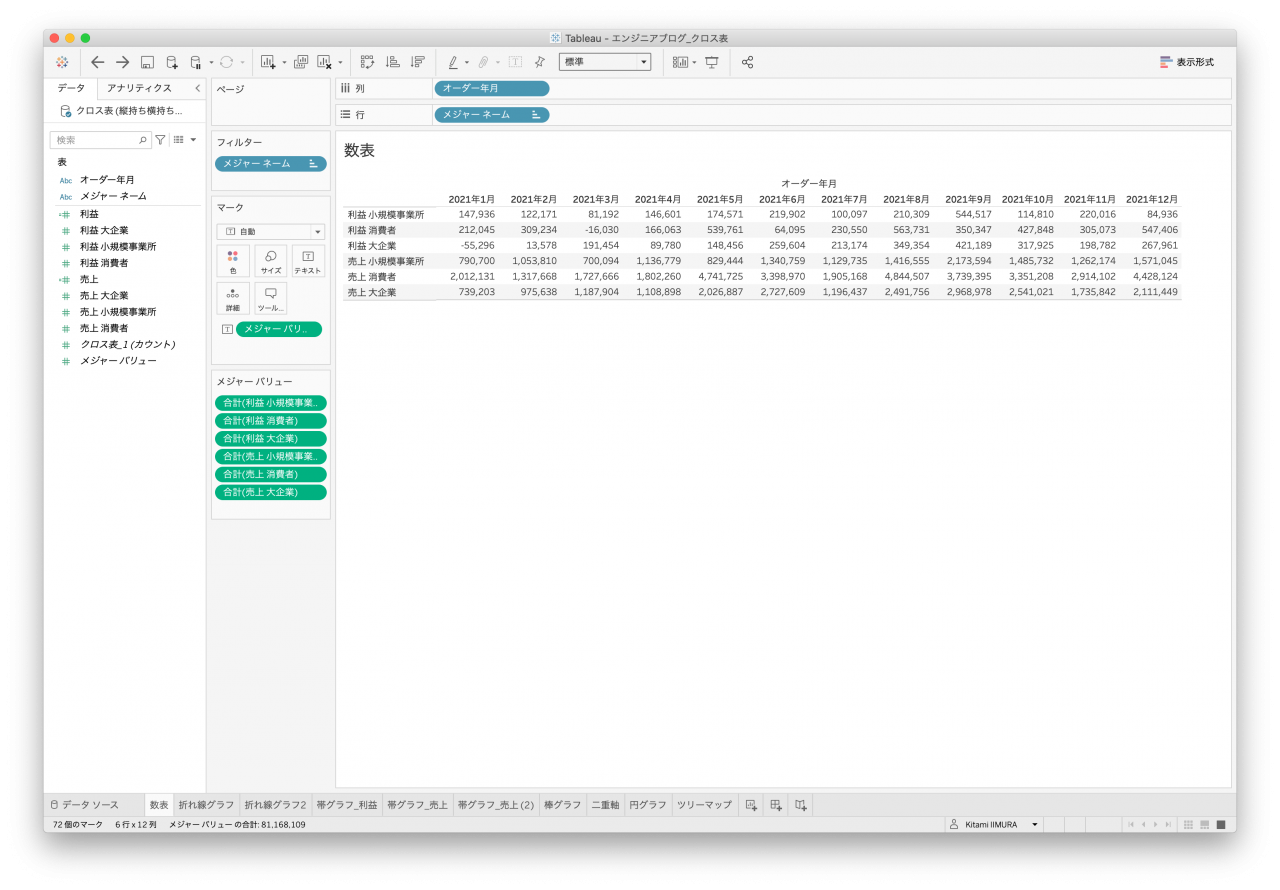
いずれのデータセットも作ることができました。ただし、クロス表データ1(図4)は区分と顧客区分が混ざっている(データ構造上、2段(2行)になっているため、Tableauのデータインタープリタ機能を使用しています。)ので区分と顧客区分が2つのヘッダーで整理されているわけではありません。文字の順序でソートされるので今回の数表は作成できますが、顧客区分の昇順などで作るのは難しいでしょう。
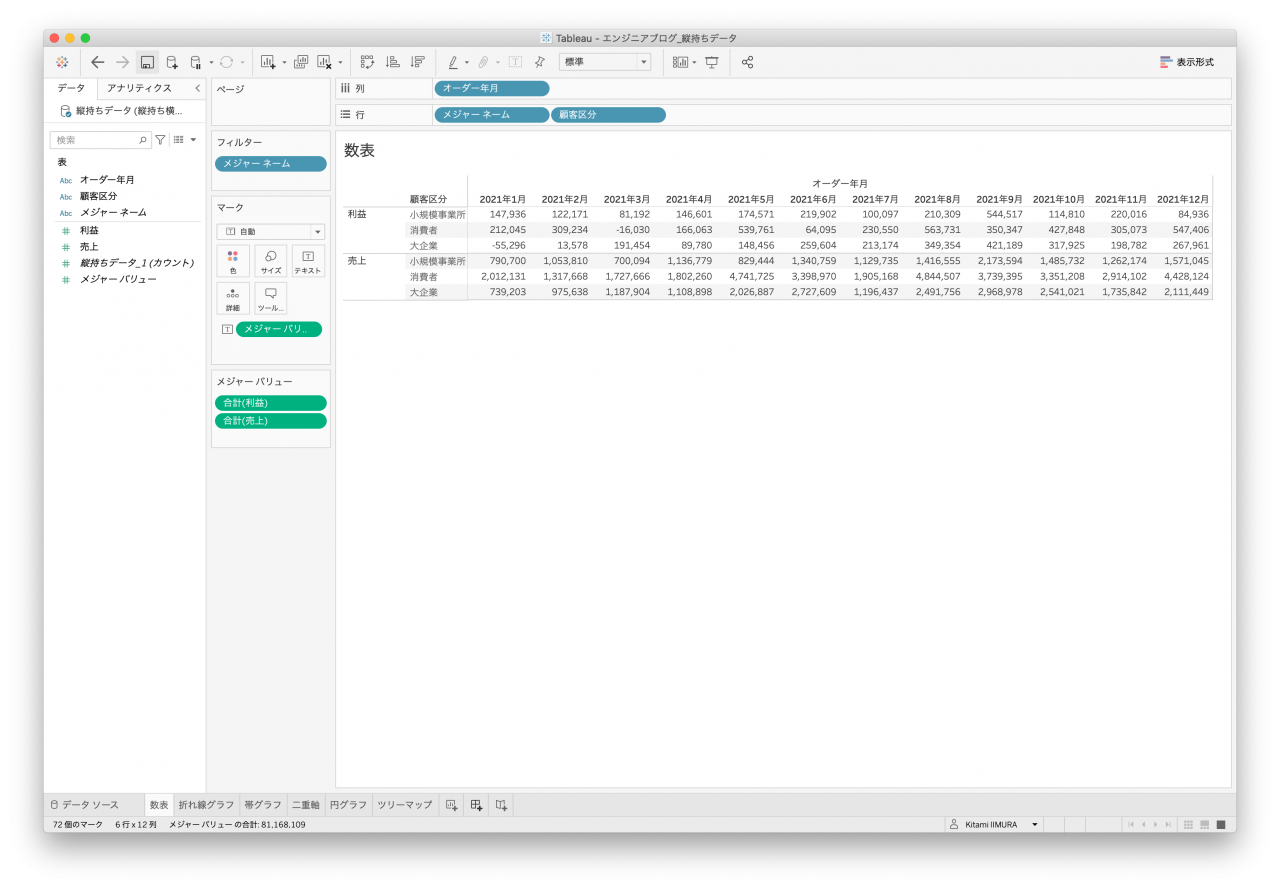
- 拡大
- 図1. 縦持ちデータ1 数表
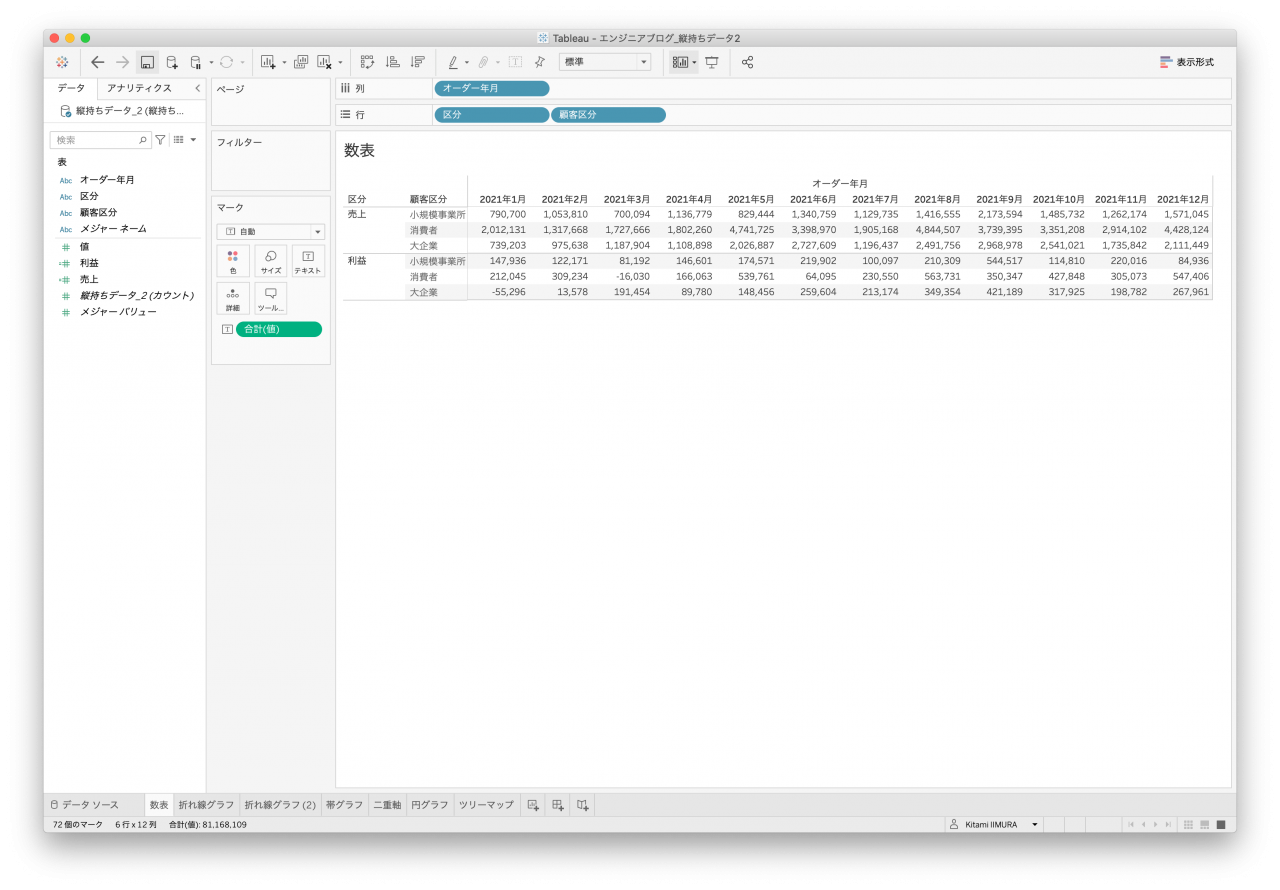
- 拡大
- 図2. 縦持ちデータ2 数表
- 拡大
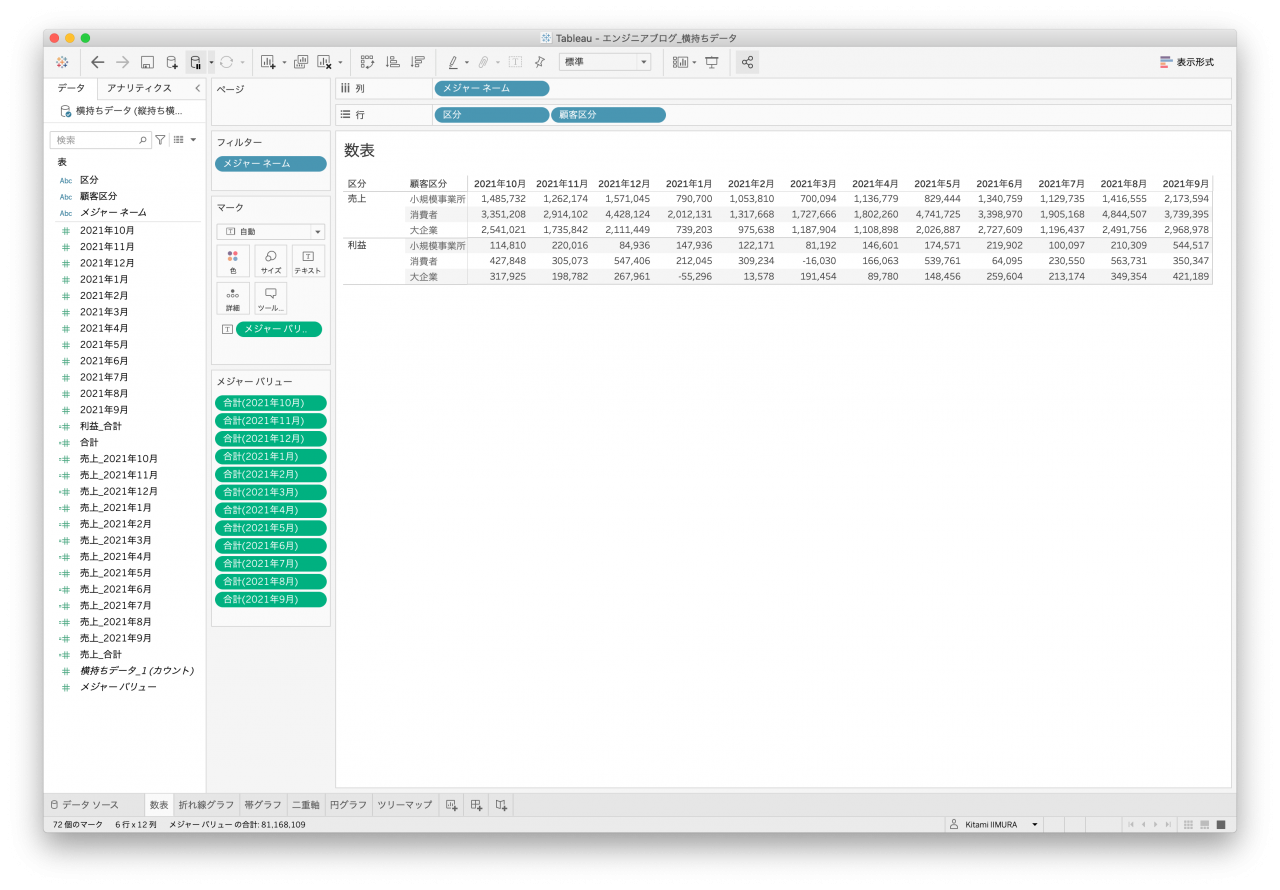
- 図3. 横持ちデータ 数表
- 拡大
- 図4. クロス表データ1 数表
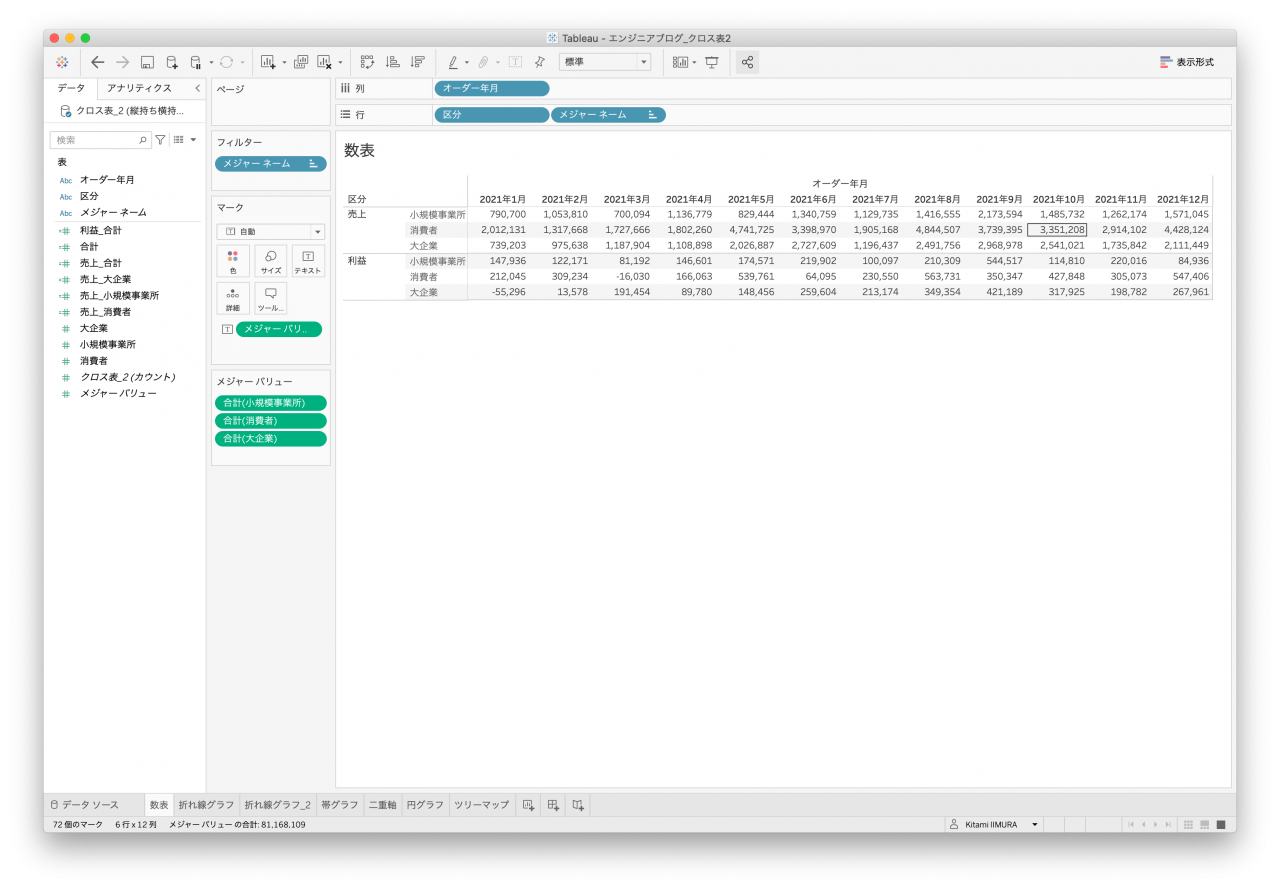
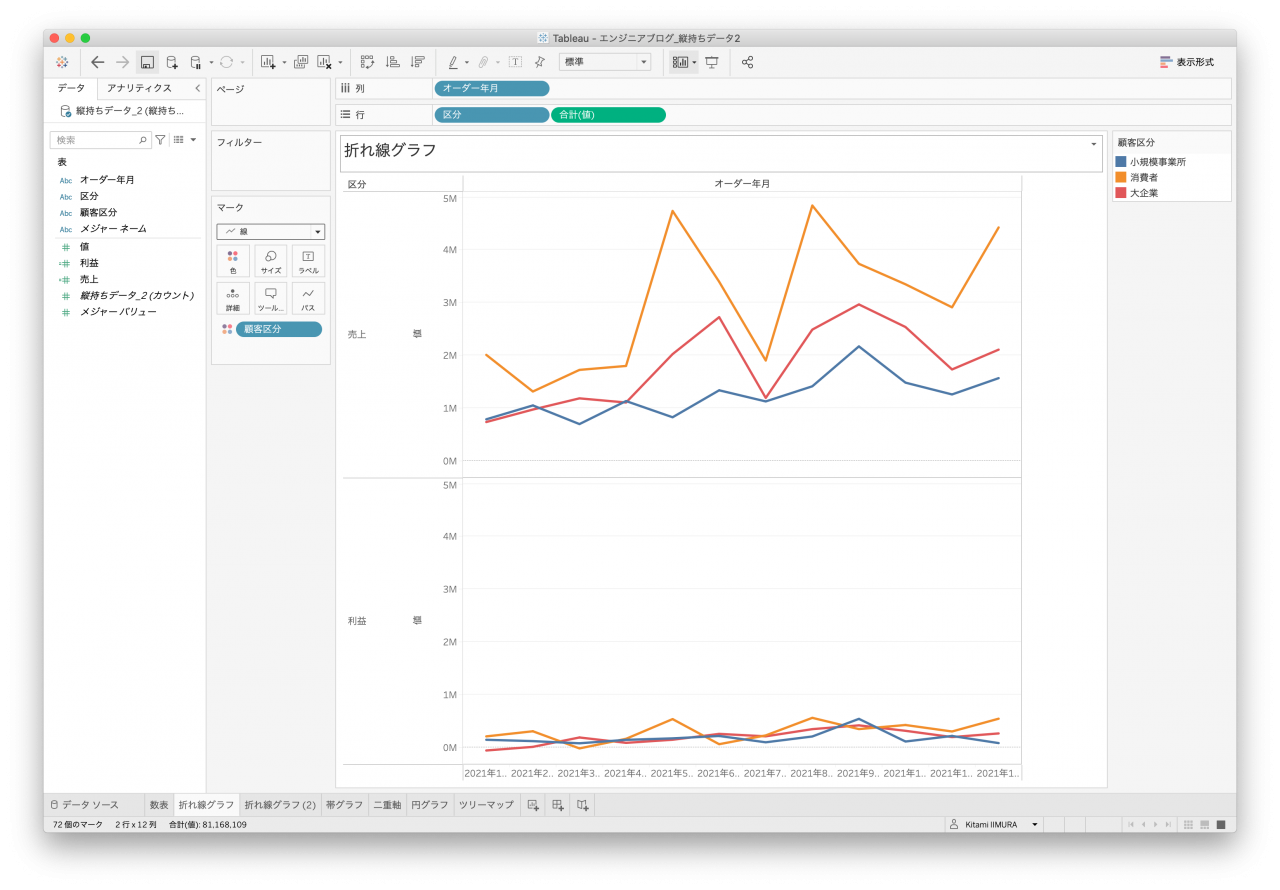
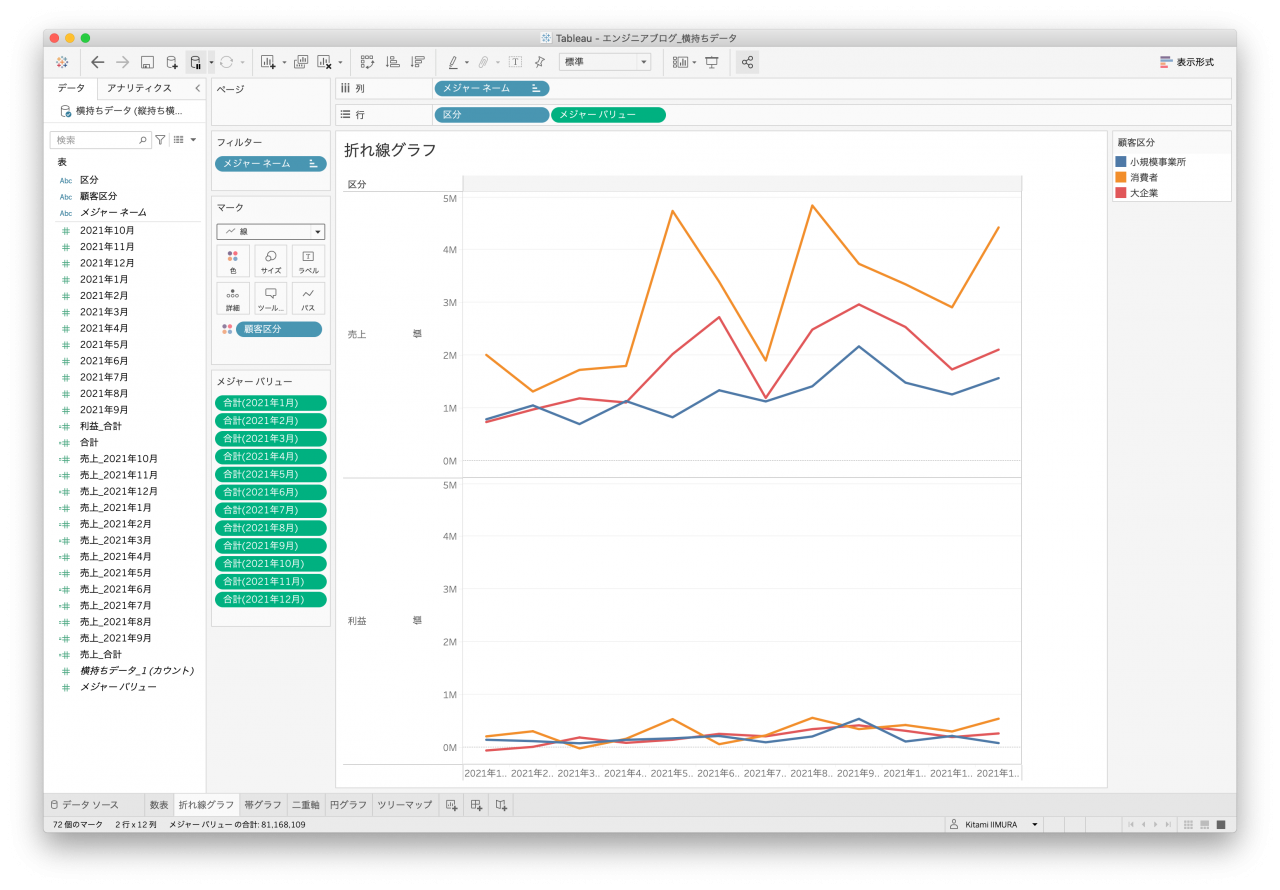
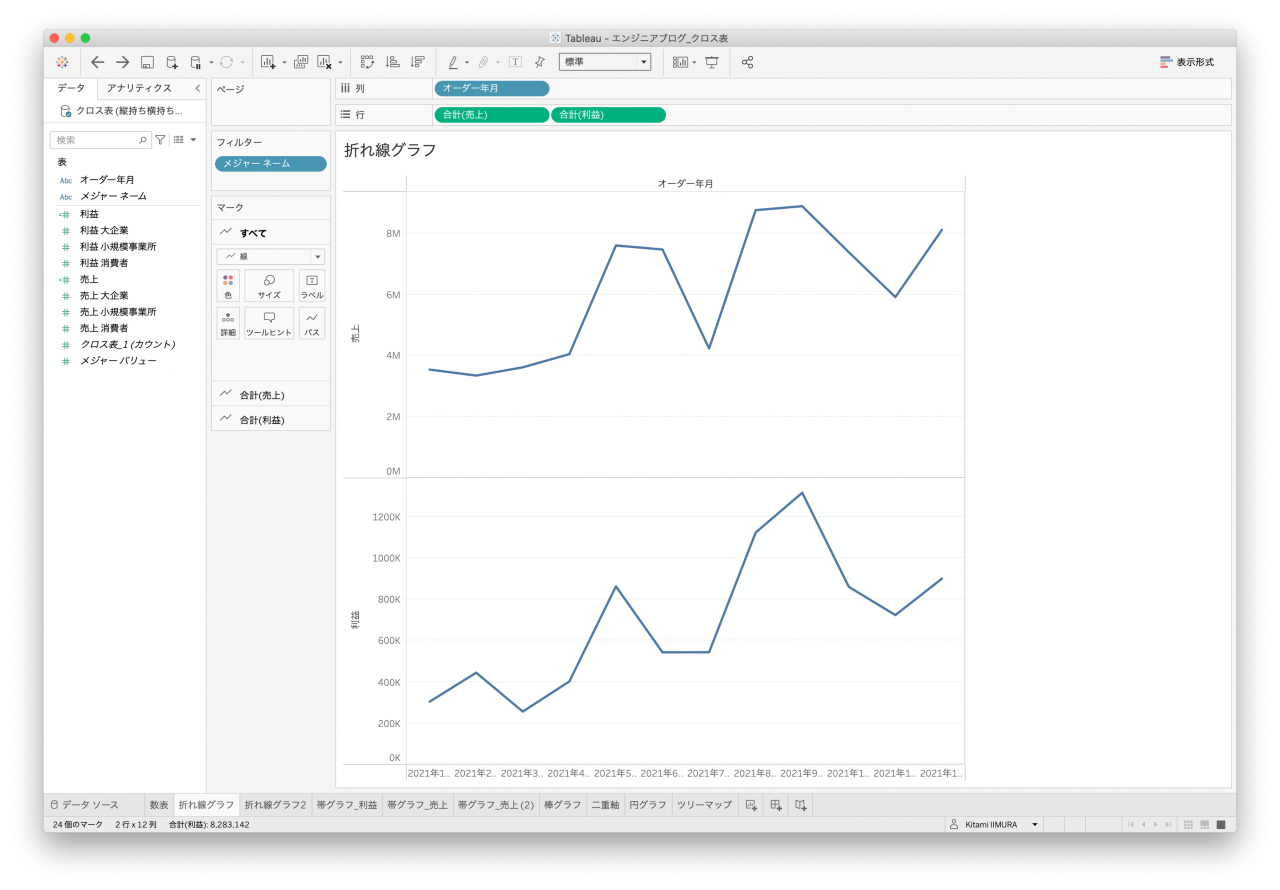
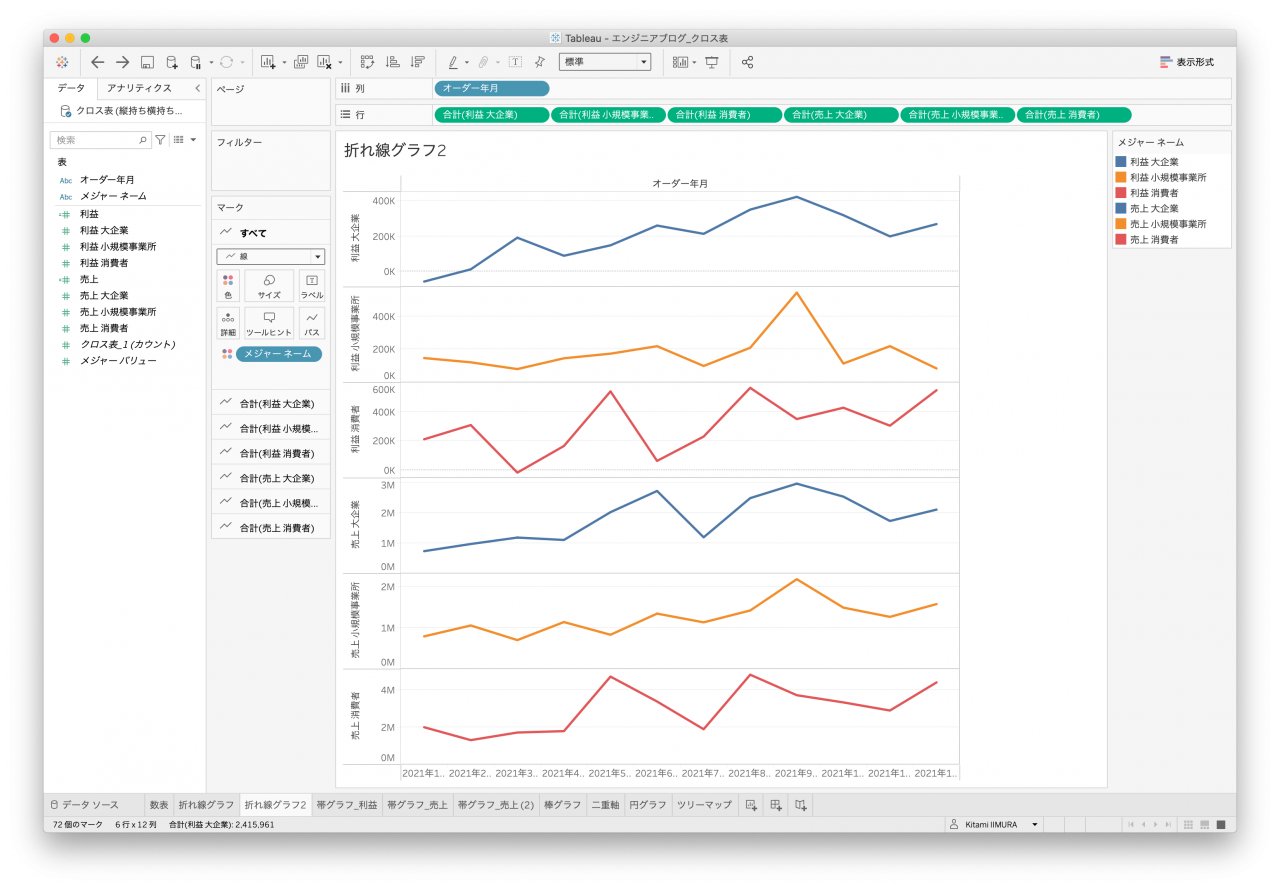
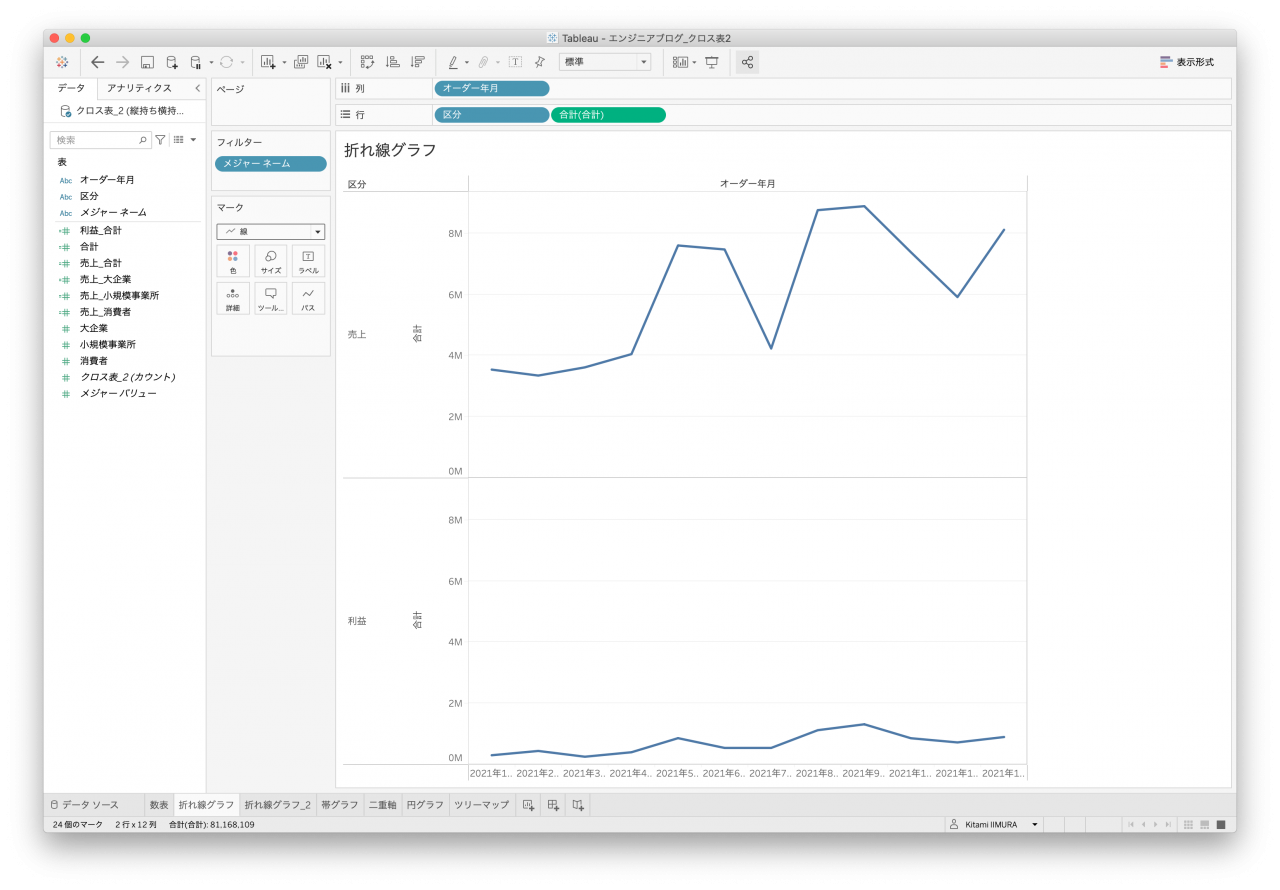
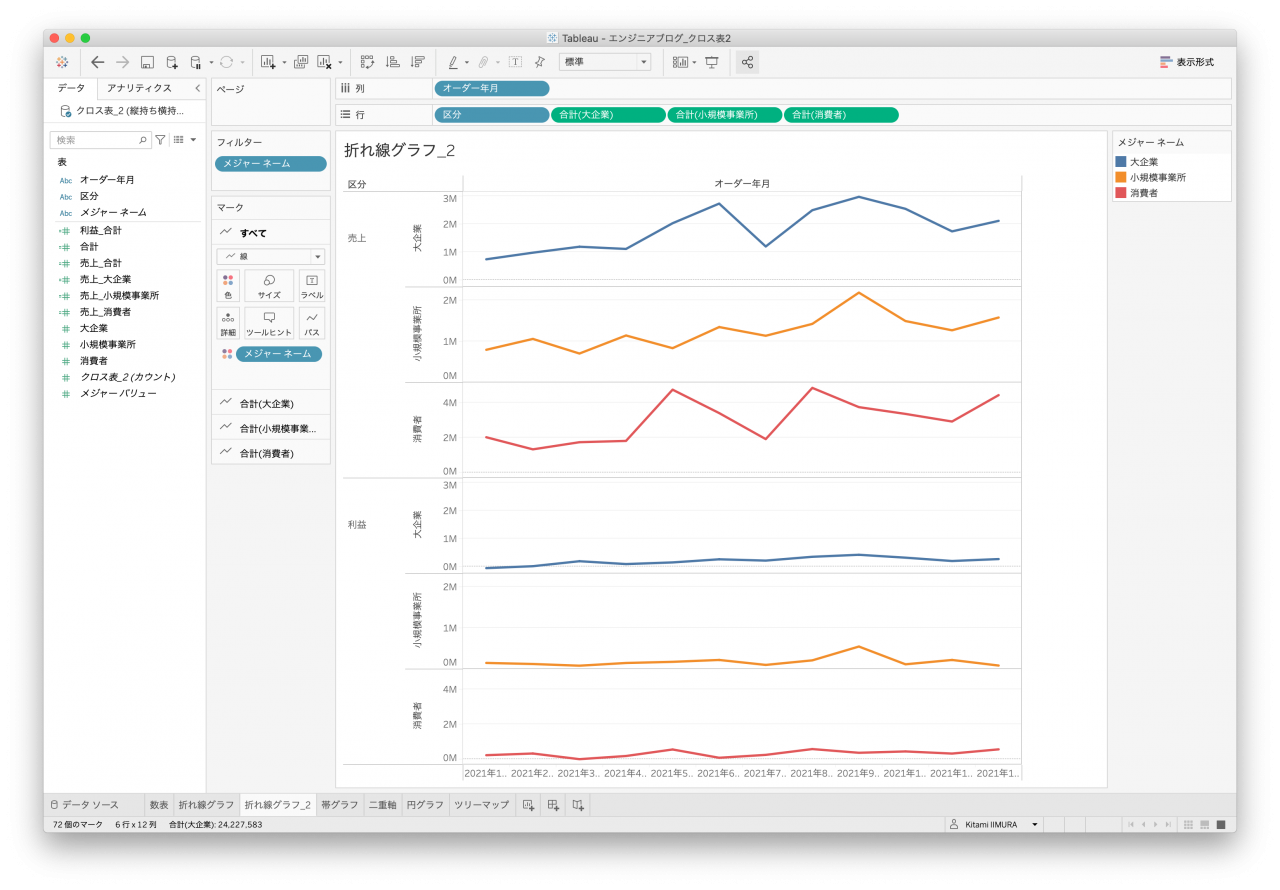
次はよく使われる折れ線グラフです。オーダー年月があるので、こちらの時系列として作成します。どのデータセットもシンプルなものは一応作れるのですが、顧客区分で色分けできないデータセットがありました。列名として値を持っていると区分にはならないので色分けすることができません(図10と図12)。
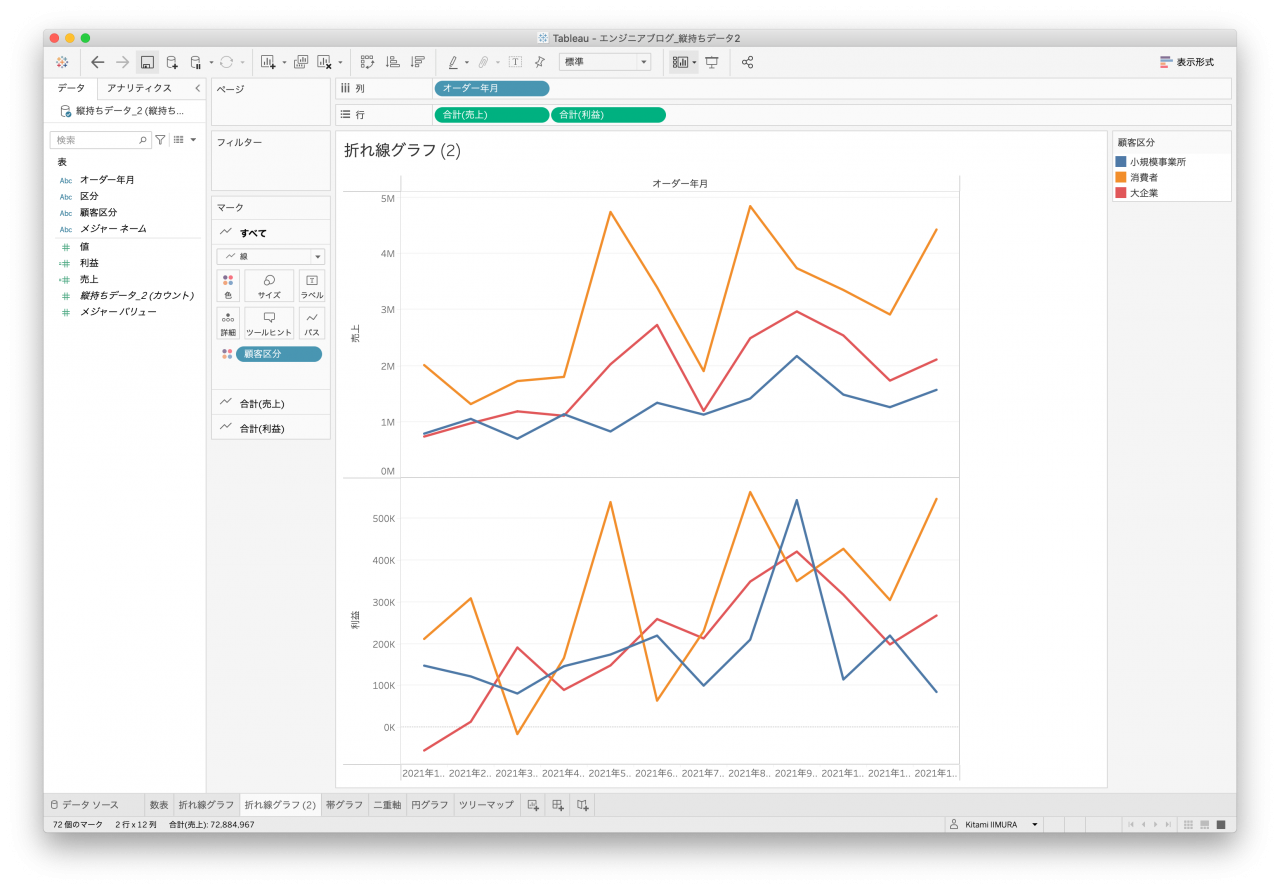
また、顧客区分が横に伸びているデータのため、クロス表はなかなか苦しいところです(図11と図13)。縦持ちデータ2は値をそのまま使うか、売上と利益に分割して使うかによって金額の軸が同じになったりならなかったりします(図7と図8)。
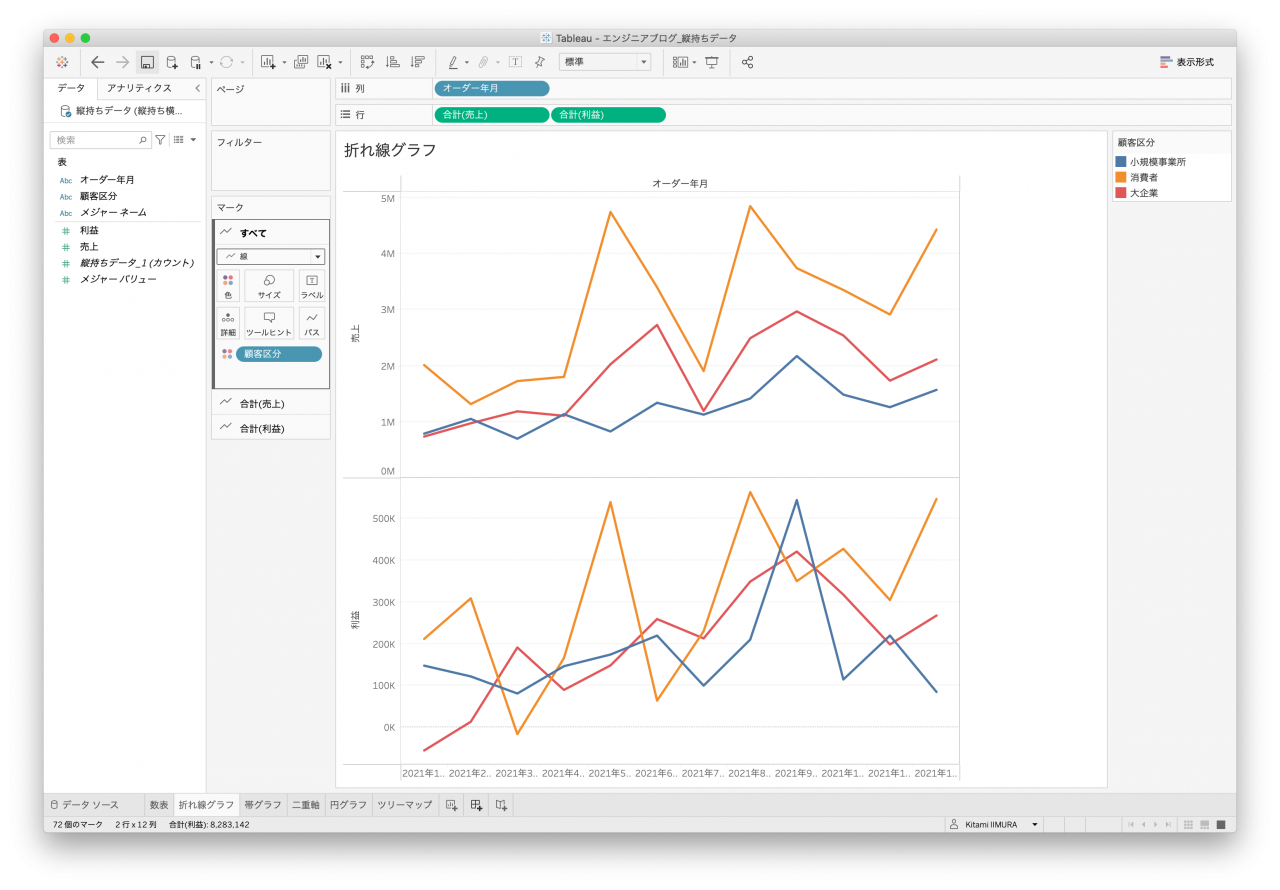
- 拡大
- 図6. 縦持ちデータ1 折れ線
- 拡大
- 図7. 縦持ちデータ2 折れ線1
- 拡大
- 図8. 縦持ちデータ2 折れ線2
- 拡大
- 図9. 横持ちデータ 折れ線
- 拡大
- 図10. クロス表データ1 折れ線1
- 拡大
- 図11. クロス表データ1 折れ線2
- 拡大
- 図12. クロス表データ2 折れ線1
- 拡大
- 図13. クロス表データ2 折れ線2
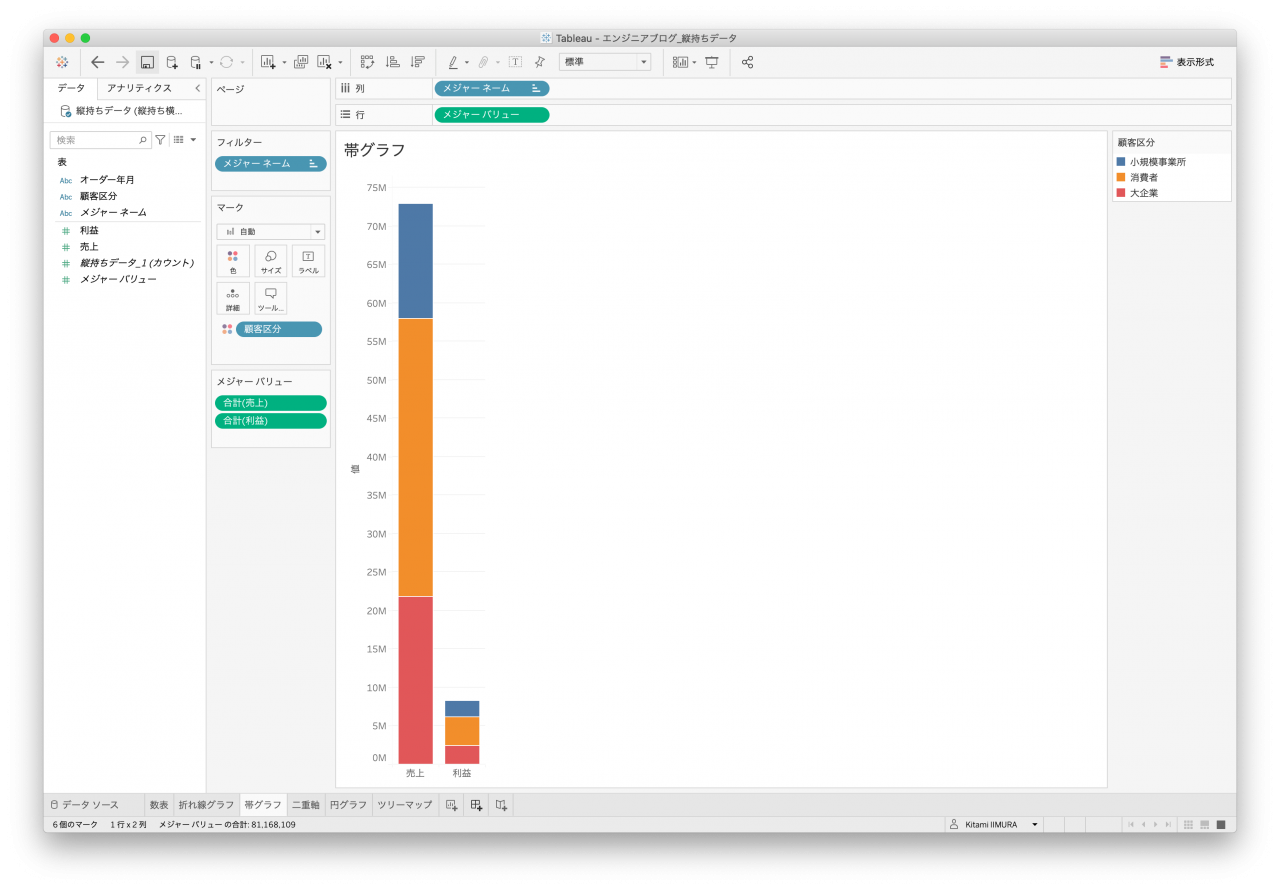
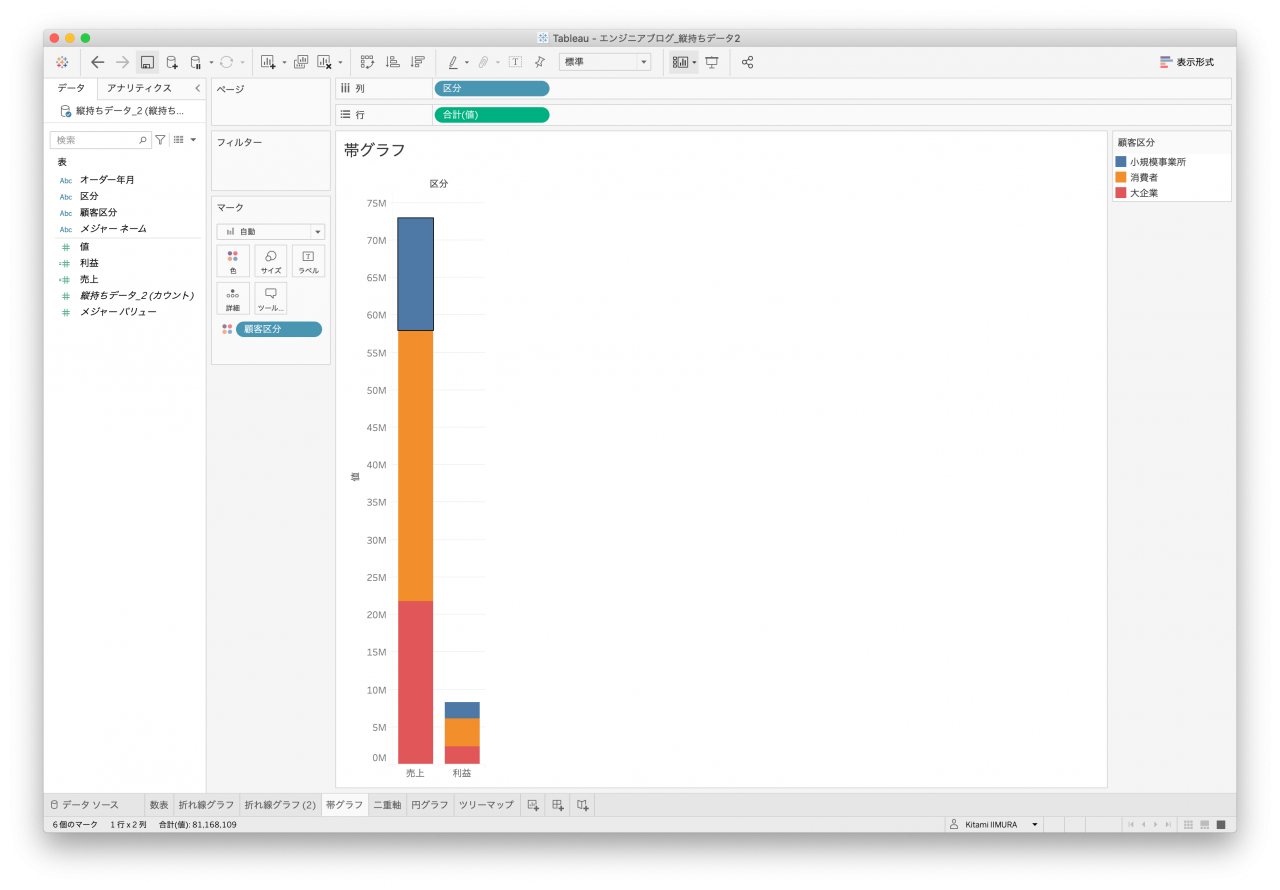
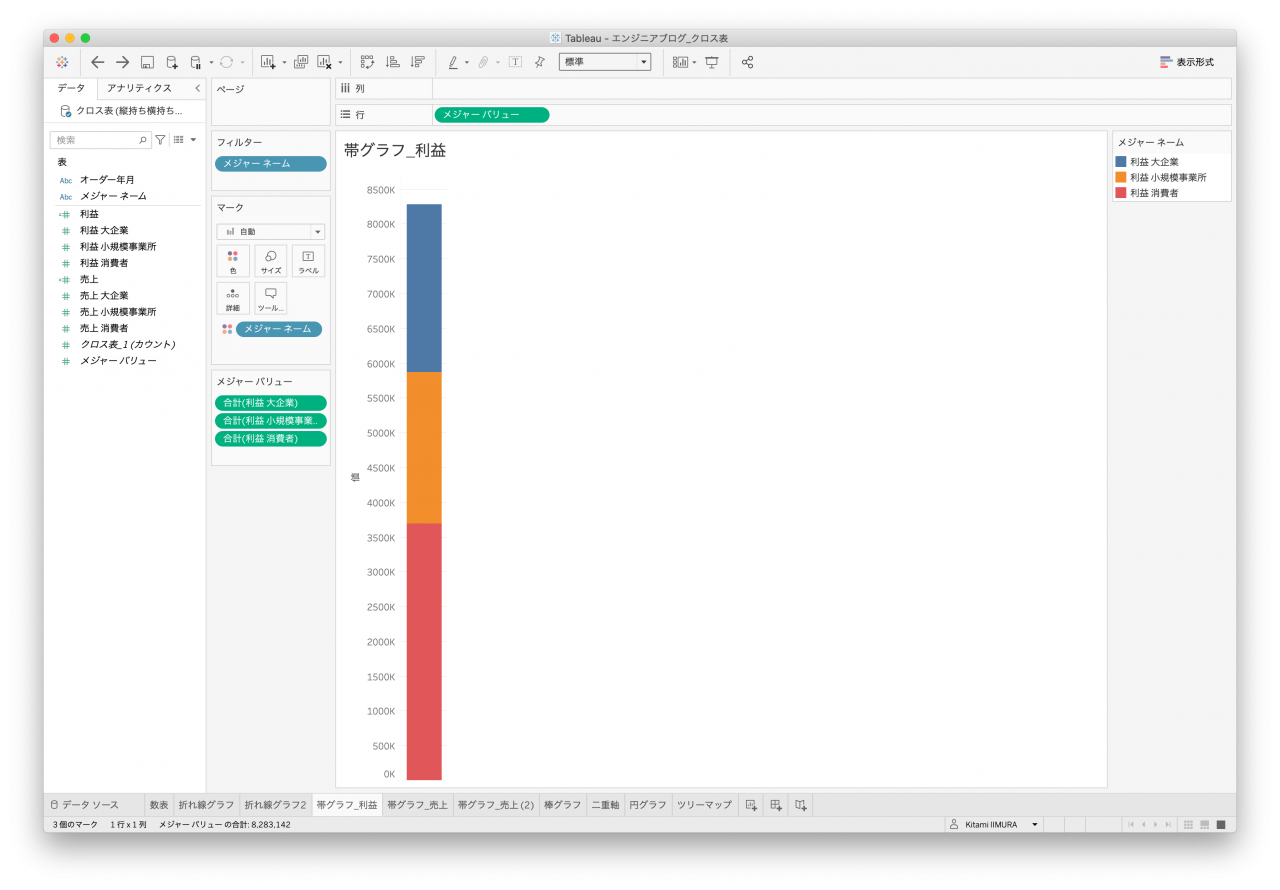
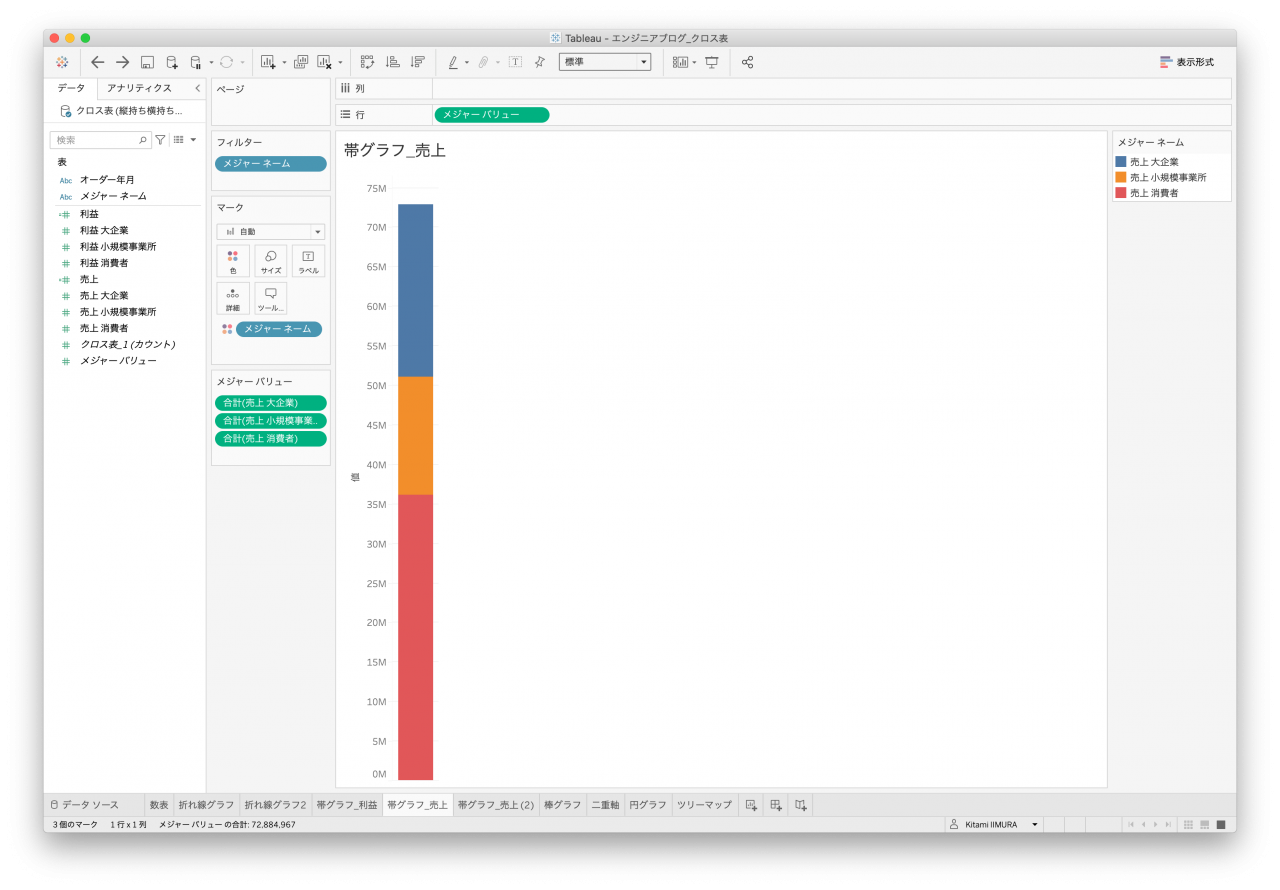
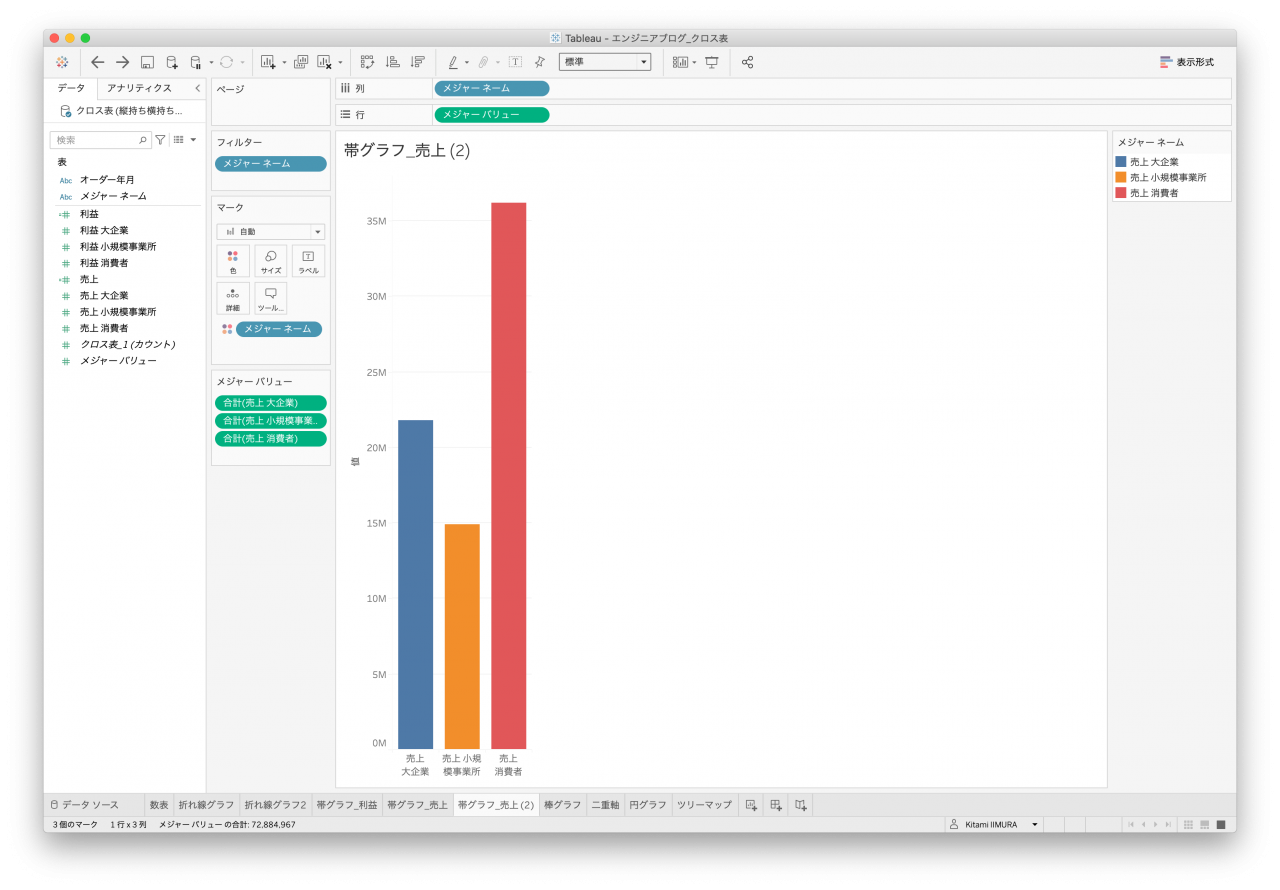
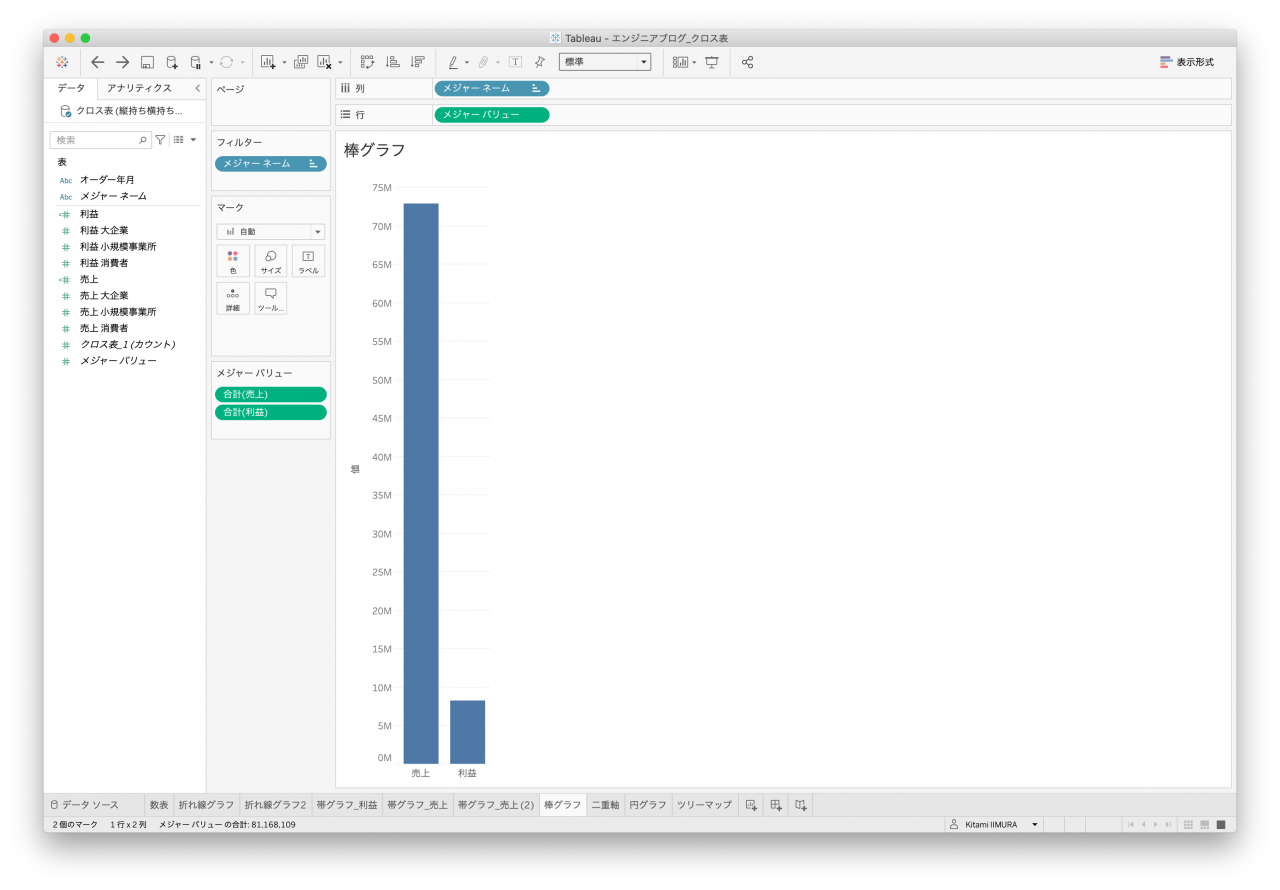
3つ目は帯グラフです。棒グラフは折れ線グラフとほぼ同じなため、こちらのグラフを作成してみます。売上&利益を区別する要素があれば良いのですが、クロス表データ1はそれがないため、売上&利益を並べて表示、かつ、顧客区分で色分けができません(図17と図18、図19、図20)。
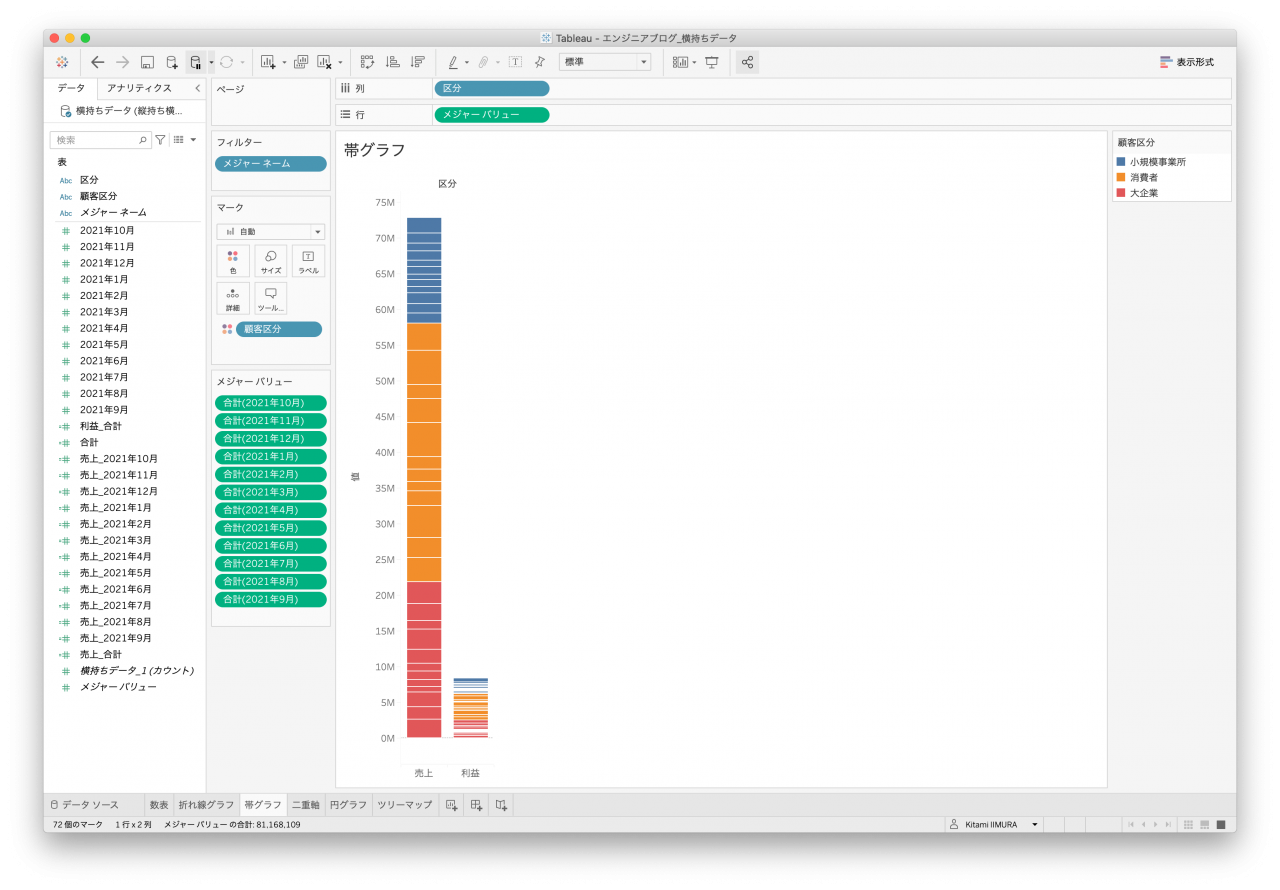
また、横持ちデータはメジャーバリューのそれぞれの列を積み上げて作成しているため、顧客区分毎の合計として表現するのは難しいかもしれません(図16。ツールヒントなどで工夫すれば出せると思います)。
- 拡大
- 図14. 縦持ちデータ1 帯
- 拡大
- 図15. 縦持ちデータ2 帯
- 拡大
- 図16. 横持ちデータ 帯
- 拡大
- 図17. クロス表データ1 帯1
- 拡大
- 図18. クロス表データ1 帯2
- 拡大
- 図19. クロス表データ1 帯3
- 拡大
- 図20. クロス表データ1 帯4
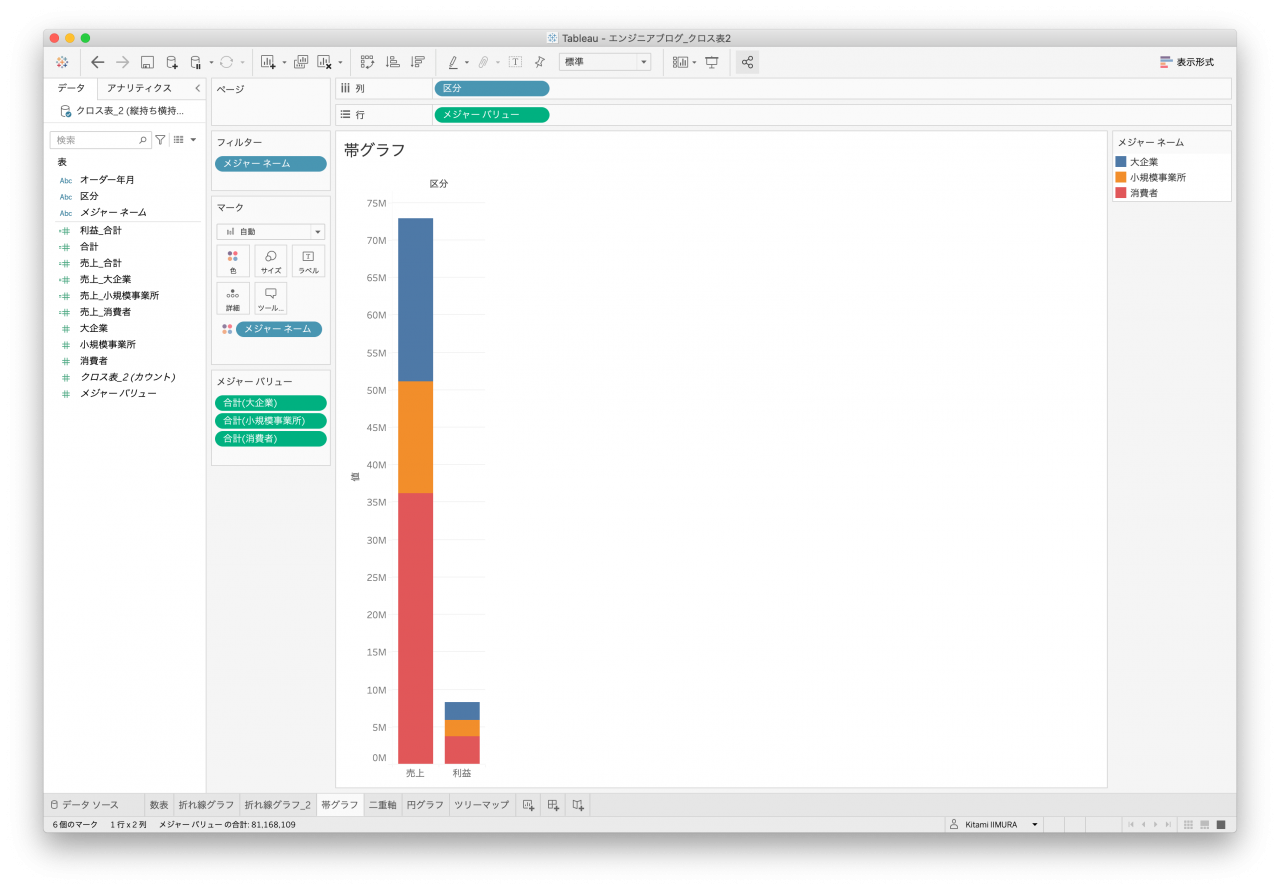
- 拡大
- 図21. クロス表データ2 帯
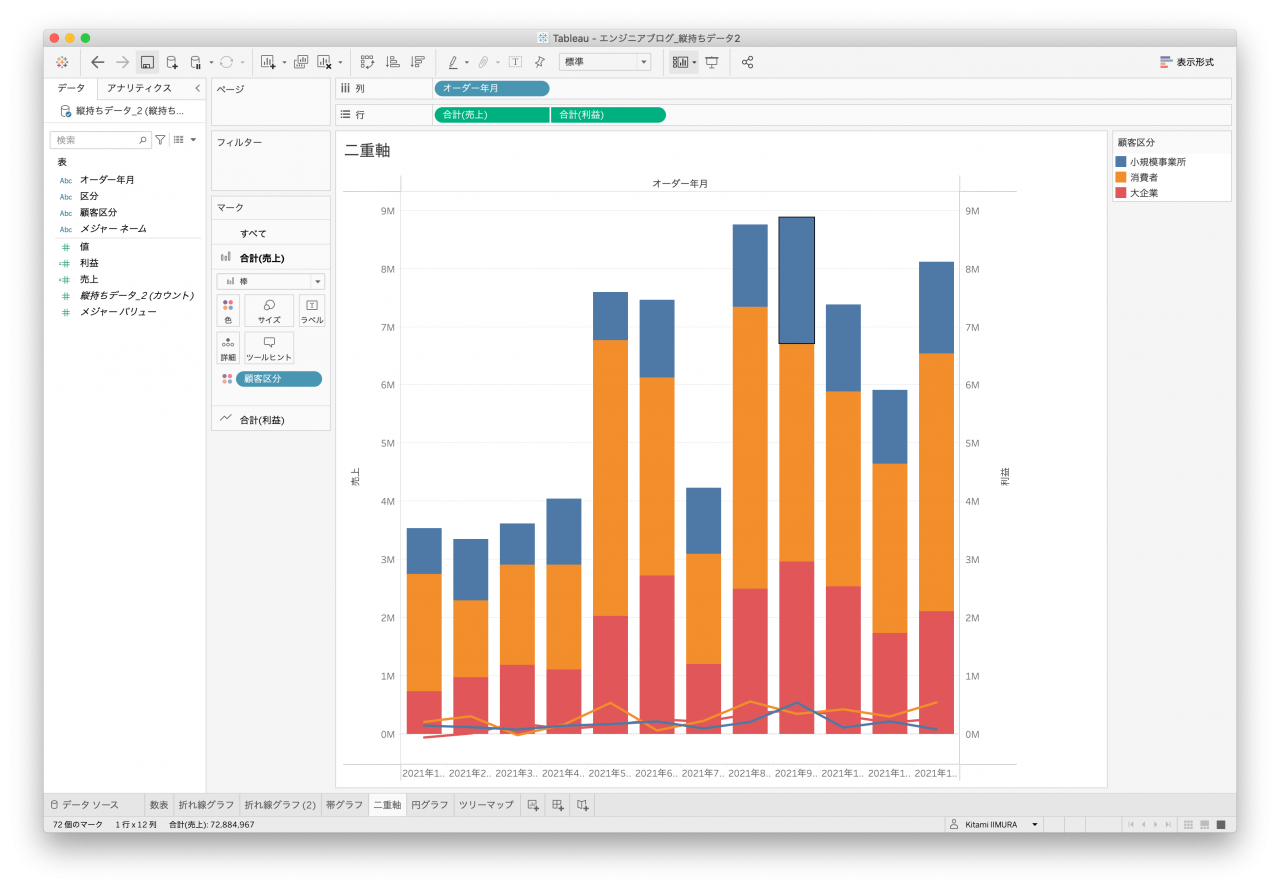
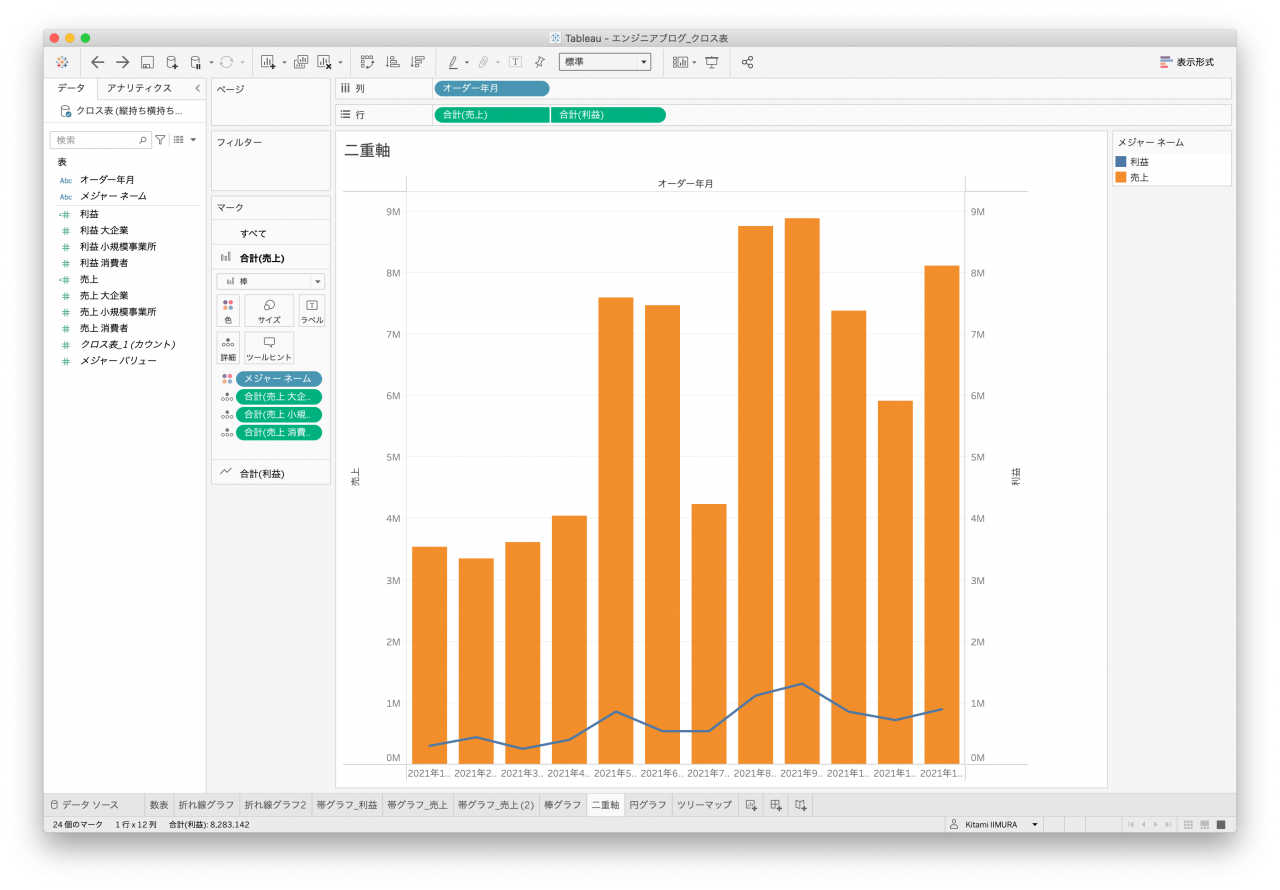
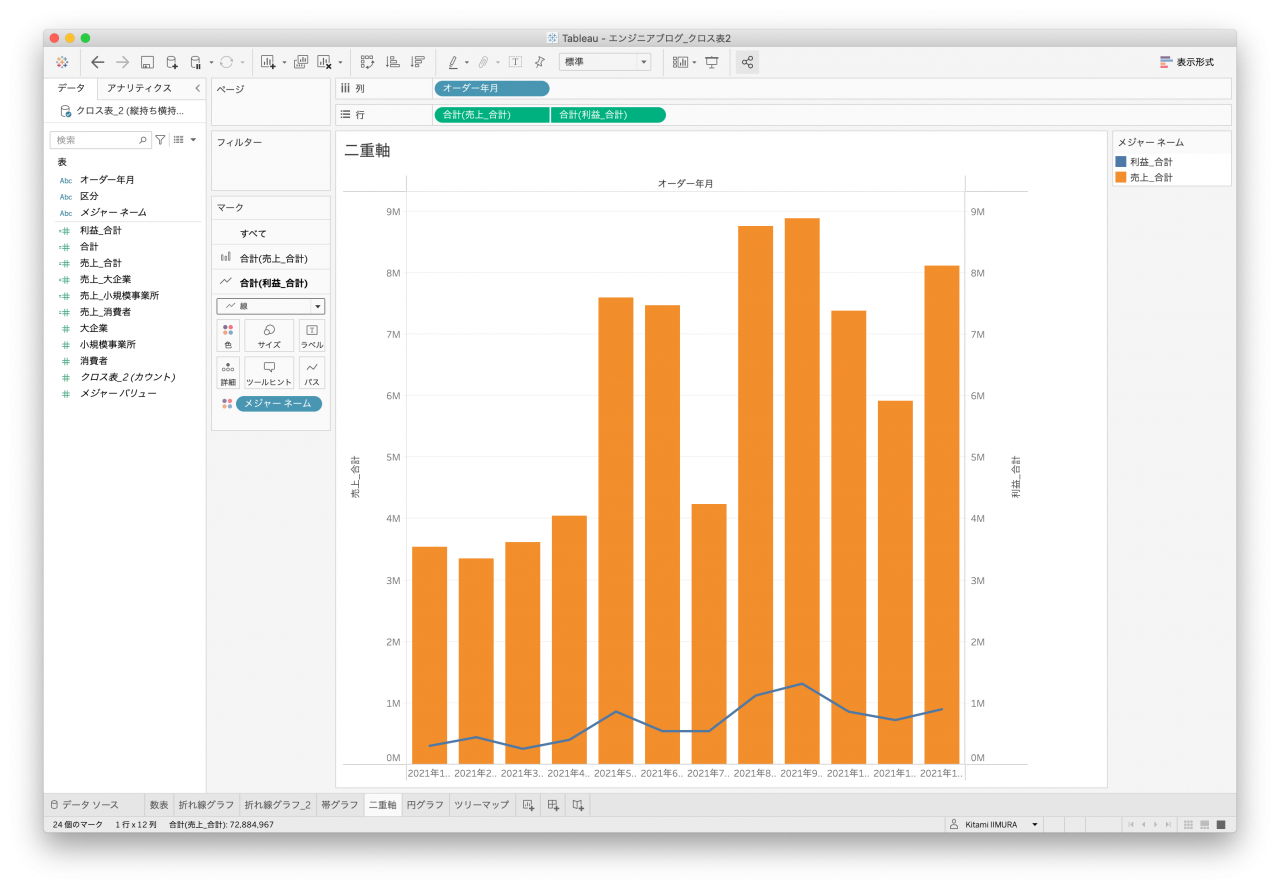
Tableauで最も使われる(?)グラフではないでしょうか。通常であれば二重軸の機能を使用して棒グラフと折れ線グラフで2種類のメジャーを表示することになります。クロス表はどちらも先ほどの帯グラフと同様に顧客区分を区別することが難しいので、単純な売上と利益の合計を表示したものになります(図25と図26)。
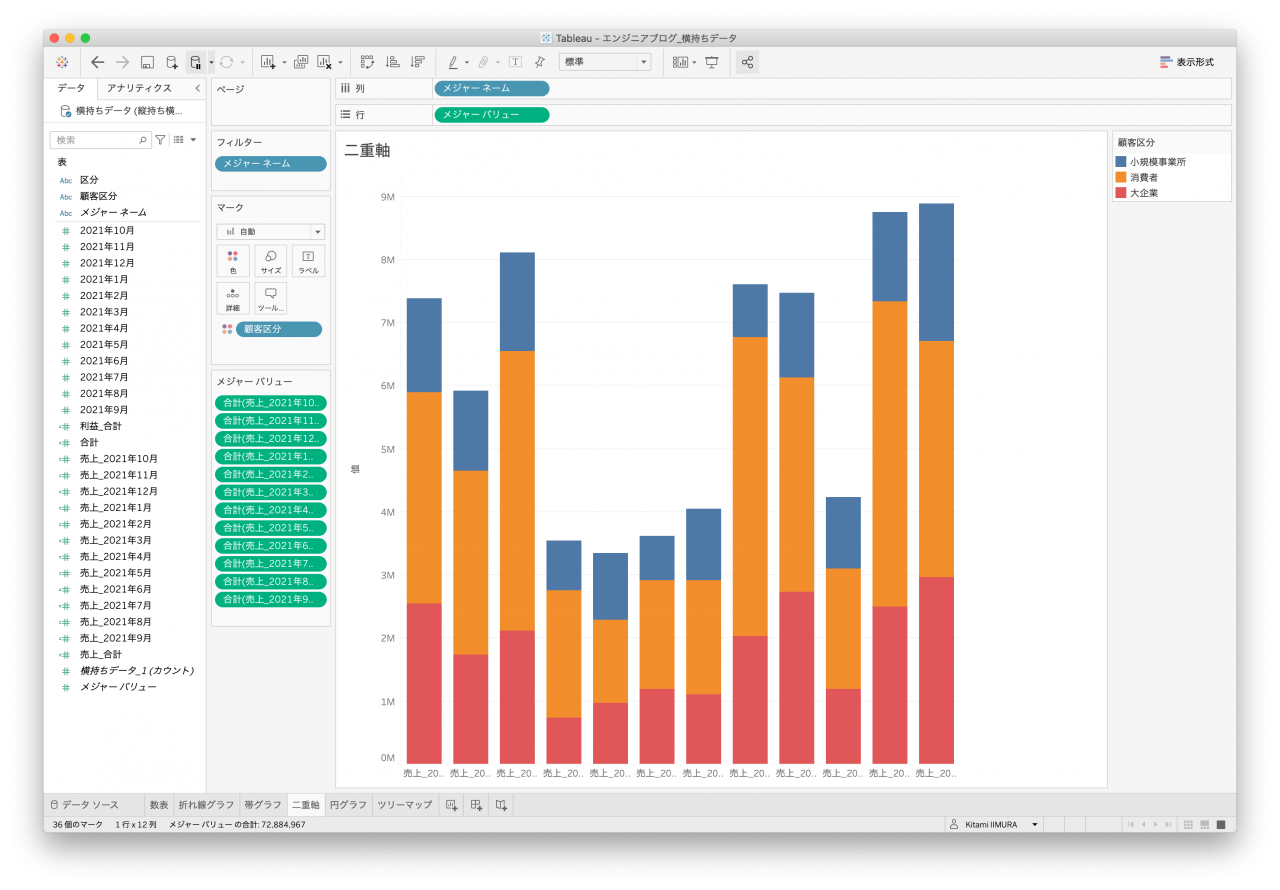
また、横持ちデータは全ての年月データ列がメジャーとして扱われるため、二重軸に必要な2つの列を選択することができません(図24)。また、売上と利益の二重軸を指定するためにそれぞれを区分別に算出して、1月から12月までの列同士を合算してしても今度は年月要素がなくなるため、全期間の売上と年月の二重軸となってしまい、年月の推移を表現することができません。
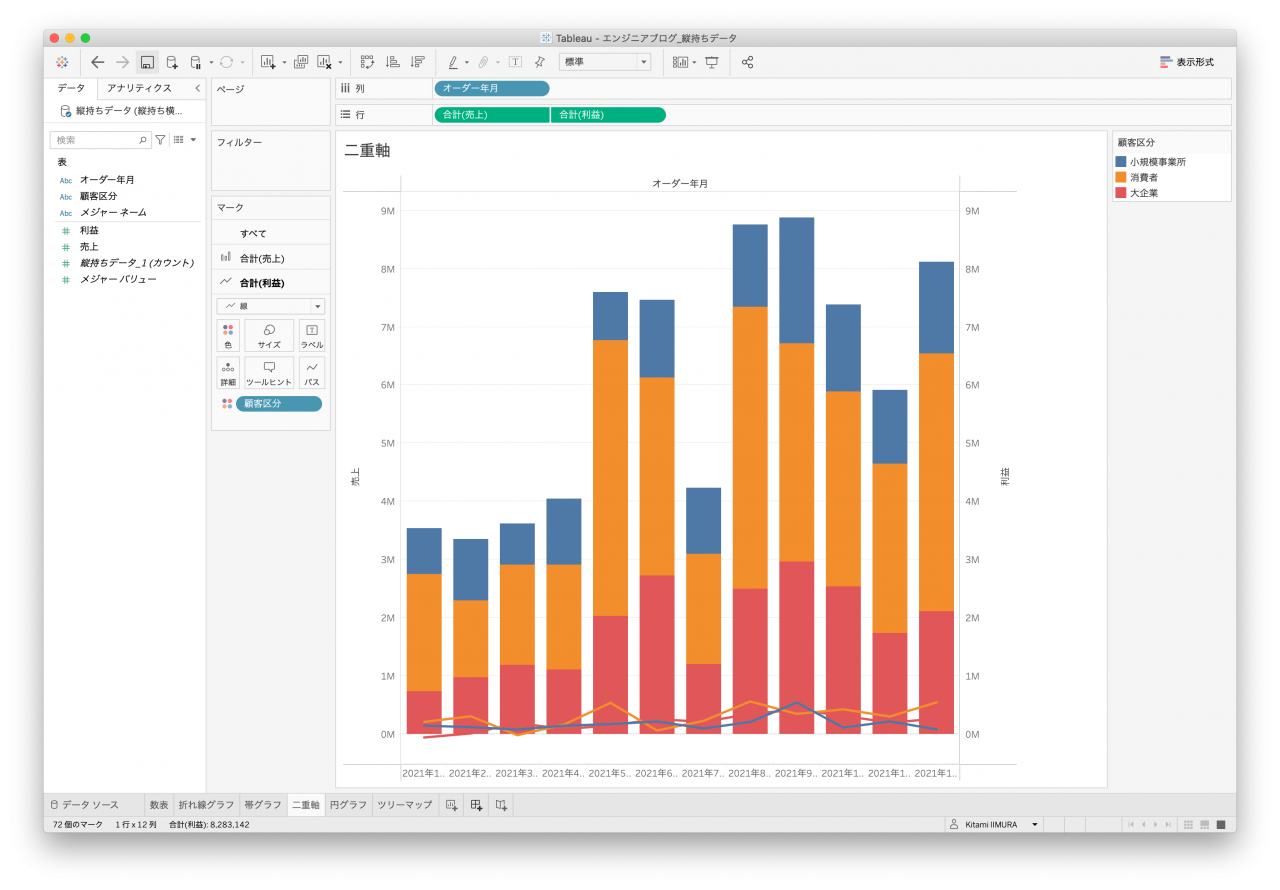
- 拡大
- 図22. 縦持ちデータ1 複合
- 拡大
- 図23. 縦持ちデータ2 複合
- 拡大
- 図24. 横持ちデータ 複合
- 拡大
- 図25. クロス表データ1 複合
- 拡大
- 図26. クロス表データ2 複合
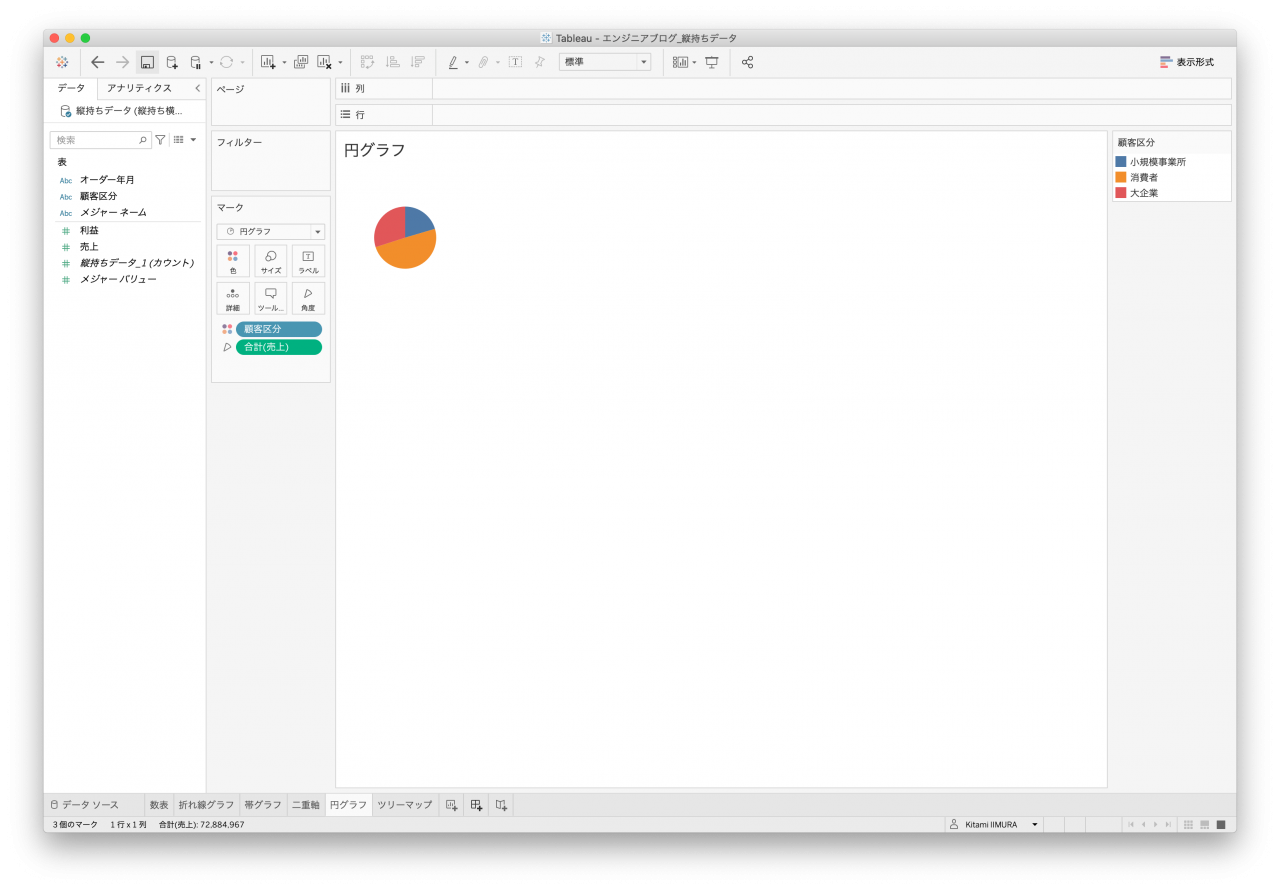
英語ではパイ(お菓子)チャートと呼ばれる円グラフです。全体における占有率を示すのに最適なグラフです。パイから切り分けられた1ピースだけ(ディメンションの値が2つ)が望ましいと言われていますが、今回のディメンションの値は大企業、小規模事業所、消費者の3つです。今回はサンプルですし大目に見てください。
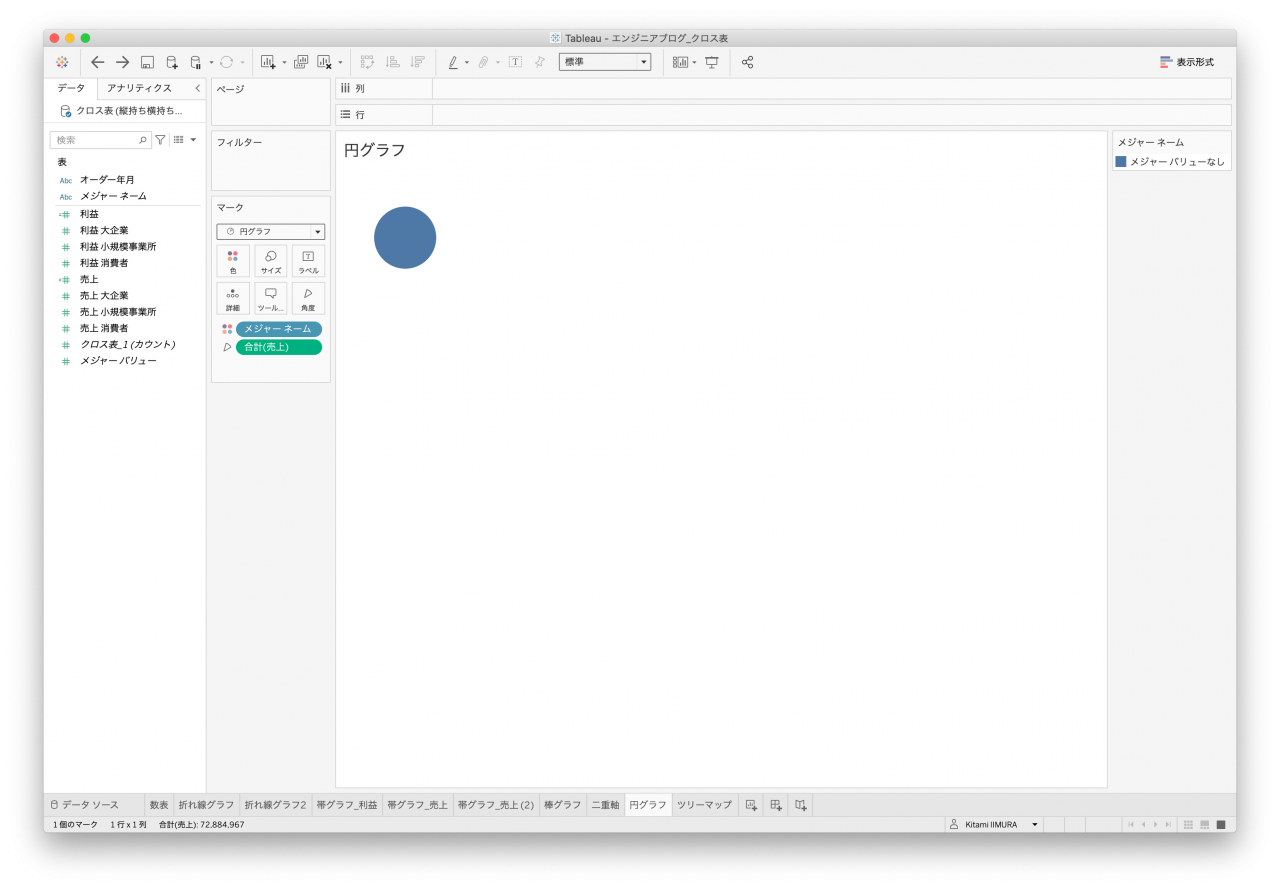
顧客区分別に色分けして出したいため、顧客区分の列を持たないクロス表データ1とクロス表データ2は作成できませんでした(図30と図31)。
- 拡大
- 図27. 縦持ちデータ1 円
- 拡大
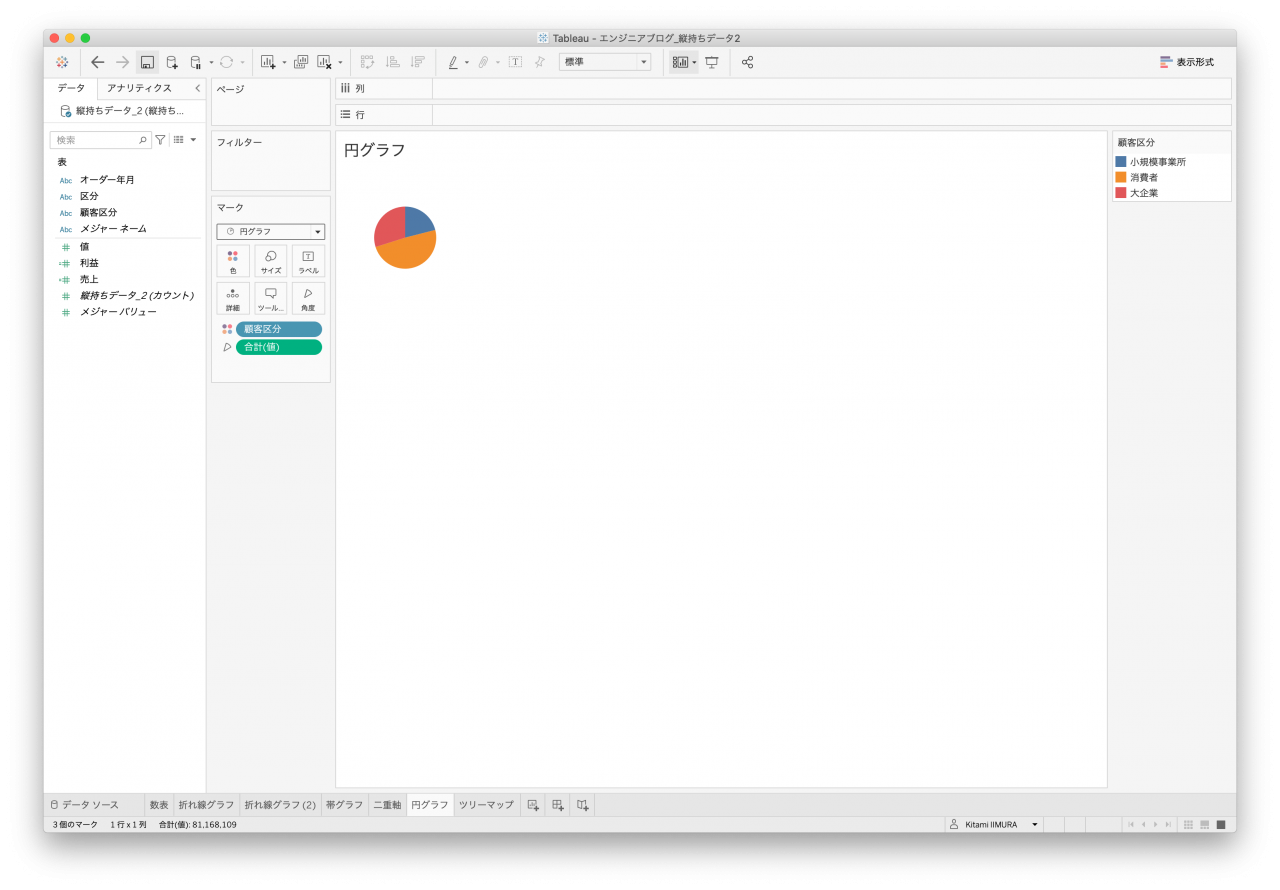
- 図28. 縦持ちデータ2 円
- 拡大
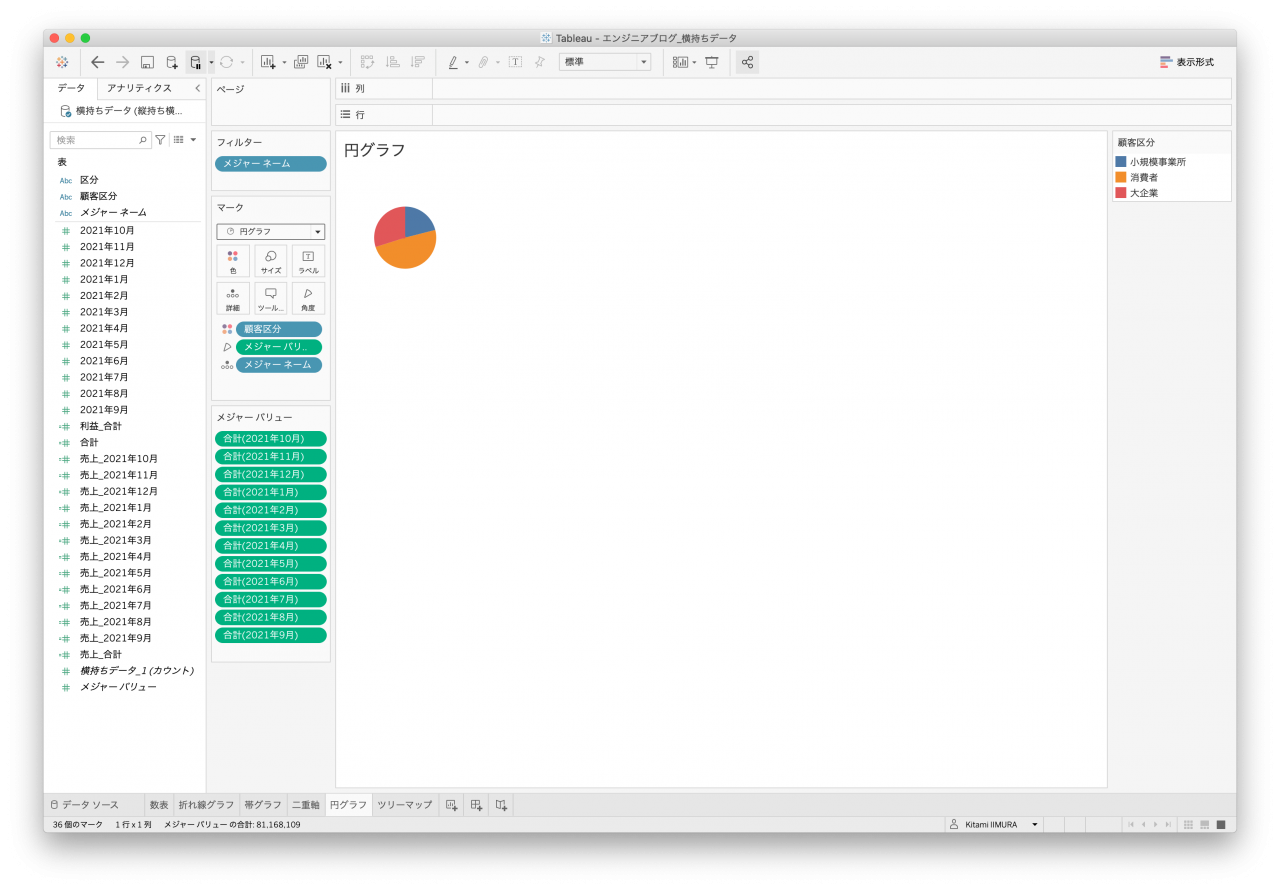
- 図29. 横持ちデータ 円
- 拡大
- 図30. クロス表データ1 円
- 拡大
- 図31. クロス表データ2 円
Tableauであればツリーマップも容易に作成でき、全体のなかでどのディメンションが大きな割合を占めているかをひと目で明らかにする(そしてその内訳もわかるようになる)グラフです。
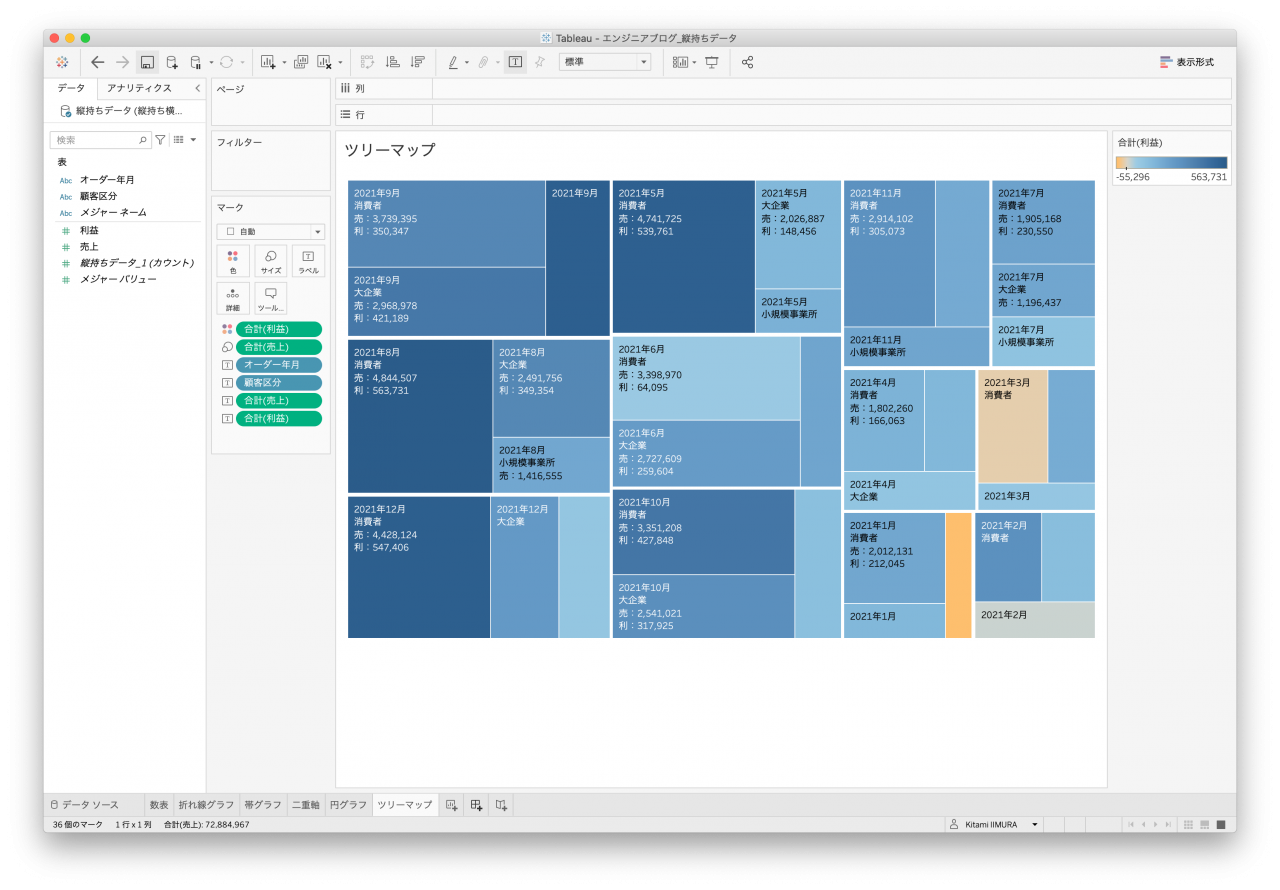
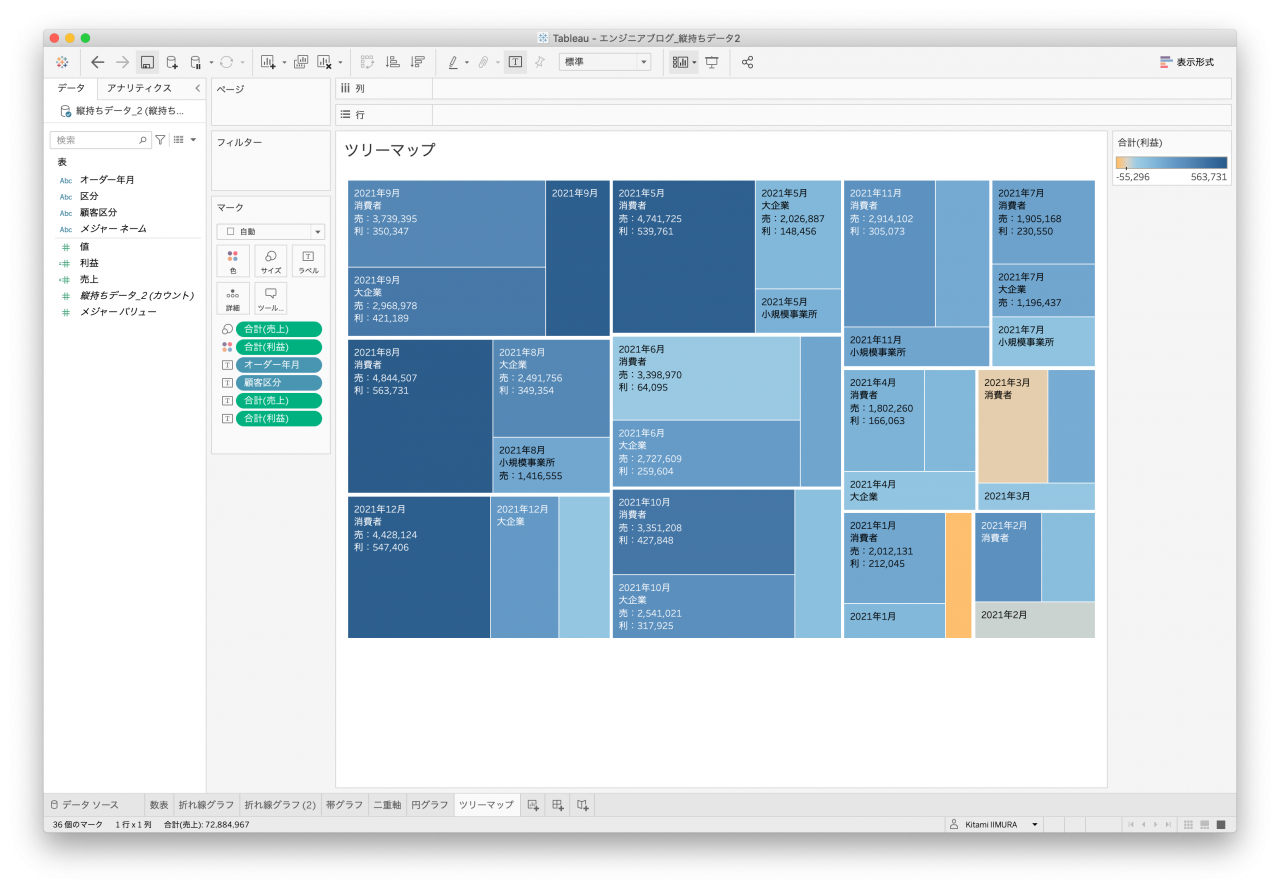
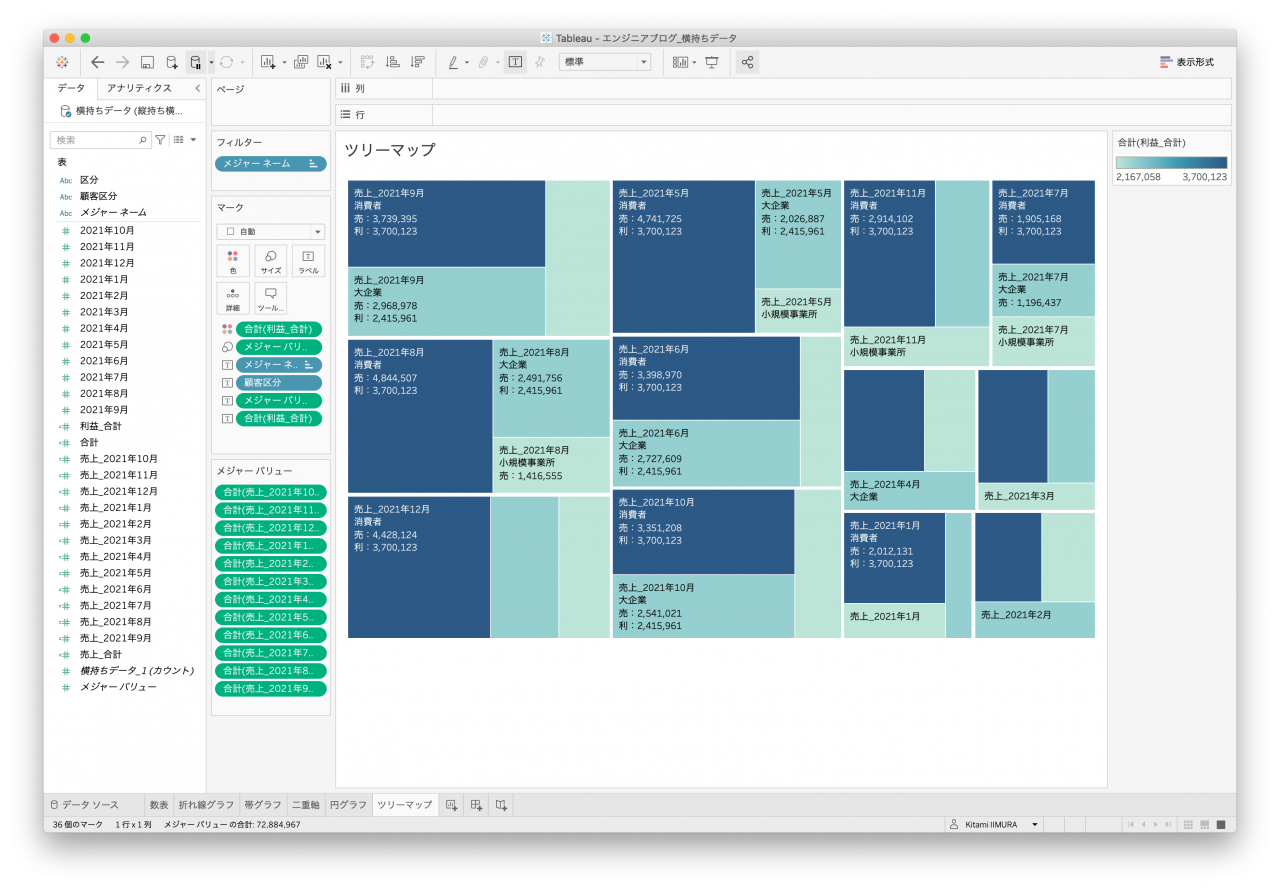
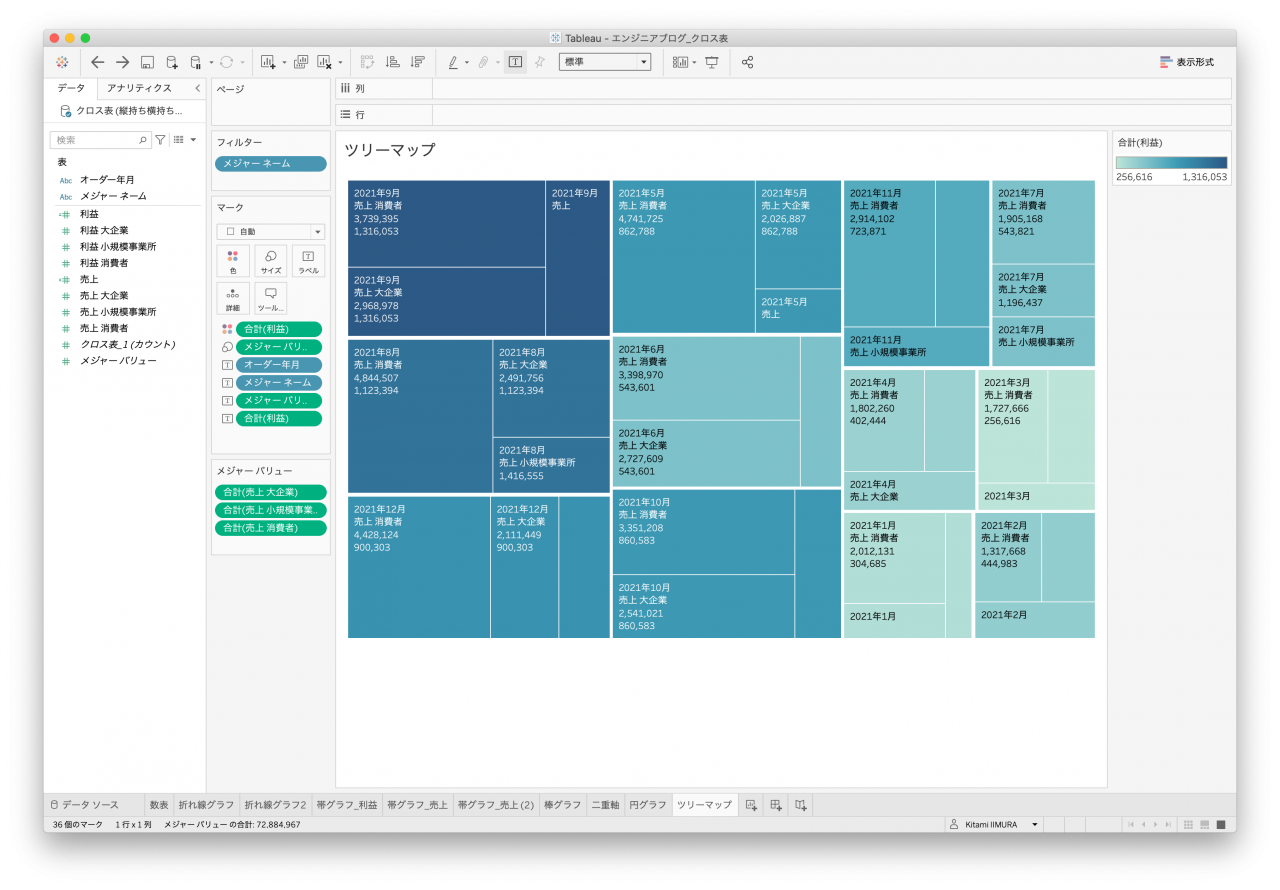
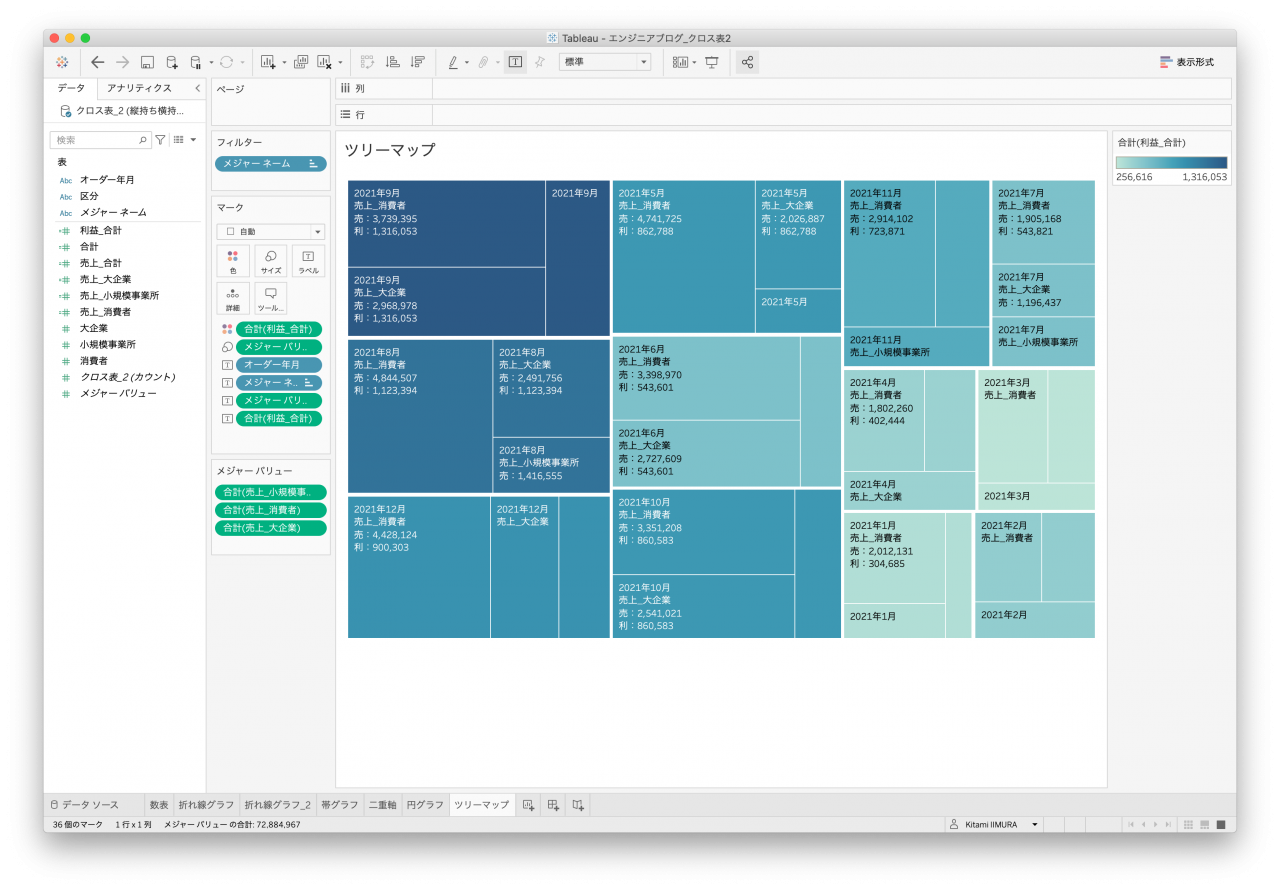
いずれもオーダー年月別、顧客区分別に作ることはできましたが、データセットによっては集計単位がどうしても期待する粒度で集計することができず、凡例(補足説明)が無いと誤解を生むグラフもありました(図34、図35、図36)。
- 拡大
- 図32. 縦持ちデータ1 ツリーマップ
- 拡大
- 図33. 縦持ちデータ2 ツリーマップ
- 拡大
- 図34. 横持ちデータ ツリーマップ
- 拡大
- 図35. クロス表データ1 ツリーマップ
- 拡大
- 図36. クロス表データ2 ツリーマップ
さて、これまで作成してきたグラフをデータ構造ごとにまとめしてみました。すぐ作成できるものは●、一部作れるが完全ではないものは▲、作れなかったものは×の評価をしています。
今回は筆者がTableauで各グラフを実装しましたが、もしかしたら作れないと書いたものの、工夫すれば作れたかもしれません。しかし、それはその時点でかなり手間がかかるということだと思いますので評価としては低い評価ということにしておきたいと思います…
表17. 各データ構造からTableauでグラフの評価を評価した表
| 【グラフ種類】 | 縦持ちデータ1 | 縦持ちデータ2 | 横持ちデータ1 | クロス表データ1 | クロス表データ2 |
| 【数表】 ディメンション ・オーダー年月別 ・顧客区分別 ・売上&利益別 |
●
|
●
|
●
|
▲
*1 |
●
|
| 【折れ線グラフ】 ・オーダー年月別 ・顧客区分別 |
●
*2 |
●
*3 |
●
*4 |
▲
*5 |
▲
*6 |
| 【帯グラフ】 ・売上&利益別 ・顧客区分別 |
●
|
●
|
●
*7 |
▲
*8 |
●
|
| 【棒と線の複合グラフ】 ・売上と利益 |
●
|
●
|
×
*9 |
▲
*6 |
▲
*6 |
| 【円グラフ】 ・顧客区分別 |
●
|
●
|
●
|
×
*6 |
×
*6 |
| 【ツリーマップ】 ・オーダー年月 ・顧客区分別 |
●
|
●
|
▲
*10 |
▲
*10 |
▲
*10 |
上記*の説明
- 表記制限あり
- 売上と利益の軸が異なる
- 売上と利益の軸はどちらでも作成できる
- 売上と利益の軸が同じ
- 顧客区分で色分けできない。
各フィールドを使用すると色分けできるが、売上ごと、利益ごとで表示ができない - 顧客区分で色分けできない
- 顧客区分内で分割されている
- 売上と利益を併記する場合は顧客区分で色分けできない。
顧客区分で色分けする場合は売上と利益を併記できない - どちらかしか表現できない
- オーダー年月ごとに利益が集計できない
これらを見ていただくと、縦持ちデータがいかにTableauで表現するのに使いやすいかがご理解頂けたかと思います。横持ちデータやクロス表データでもある程度のグラフは作れますが、制約があったり、計算フィールドを駆使して作らなければいけなかったり、そもそも期待する表示ができなかったりということがわかるでしょう。
これまで見てきたように、データ構造は様々であることと、その中でもTableauで表現するのに適したデータ構造は縦持ちであるものの、表現したい目的によっては縦持ちでもさらに持ち方を工夫しなければならないことを説明してきました。この記事が少しでも皆様のデータ分析活動にお役に立てれば幸いです。