こんにちはSEC2年目のmasatoです。
業務で機械学習やAIに触れることが多く、積極的に情報を集めています。
その中で、私が注目している技術である「リザバー計算」について書いていきます。
早速ではありますが、リザバー計算について簡単に説明します。
リザバー計算は、簡単に言えば
「時系列データを使った分類や予測が低コストで高速に学習できる」計算です。
深層学習モデルよりも低い学習コストで、深層学習モデルに近い計算性能を持っているのが大きな特徴です。
では、どのような仕組みでしょうか。簡潔にいうと
「リザバー計算は、時系列の入力を、リザバーというものを用いて、
入力を時空間パターンに変換し、線形学習器などの簡便な学習アルゴリズム
によってパターン解析を可能にすること」
です。流れとしては以下のようになります。
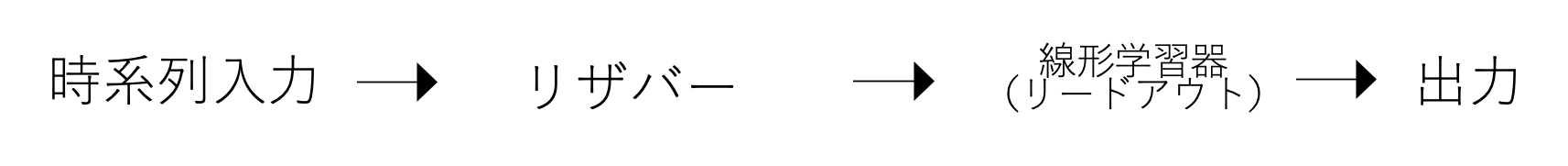
おそらく、これだけでは理解できないと思います。
ですので、この文章を理解できるように具体例で読み解いていこうと思います!
さてまずは、「リザバー」とはなんなのでしょうか。それを説明していきます。
リザバーは英語でReservoirと書きます。
これは貯水池という意味です。なのでそのまま直訳するとリザバー計算は「貯水池を用いた計算」という意味になります。
実際にリザバー計算は、ソフトウェア的な実装だけでなく、現実の容器の中の水を利用した計算でも利用可能です。(さらに、リザバーをタコの足にして計算することも可能です!今回は軽く触れただけですが、ソフトウェア以外で計算できるのは深層学習にはない特徴です。)
ですので、これから説明で用いる蓄えられた水を「リザバー」とまずは解釈してください。
次に、「時系列入力」とはなんでしょうか。時系列とは、「時間の順序に従って連続的、あるいは非連続的に並べられている系列」のことです。例えば、「時間の経過による気温の変化のデータ」や「定期的に計測される自分の身長の変化のデータ」などです。
今回の例では、リザバーが蓄えられた水だったので、蓄えられた水に、石を順番に投げ込んでいくとします。石を今回は単純に「重さ」の数値データとして扱うと「時間の経過による重さの変化の系列データ」として考えることができます。
このように石の系列を順番に投げ込んでいくのが、この場合の「時系列の入力」です。
さて、時系列である「石の系列」をリザバーである「容器の水」に石を投げ込むことで入力していくとどうなるか説明していきます。
まずは、容器の静かな水面を想像していただきたいです。その中に、石を投げ込むと波紋ができると思います。
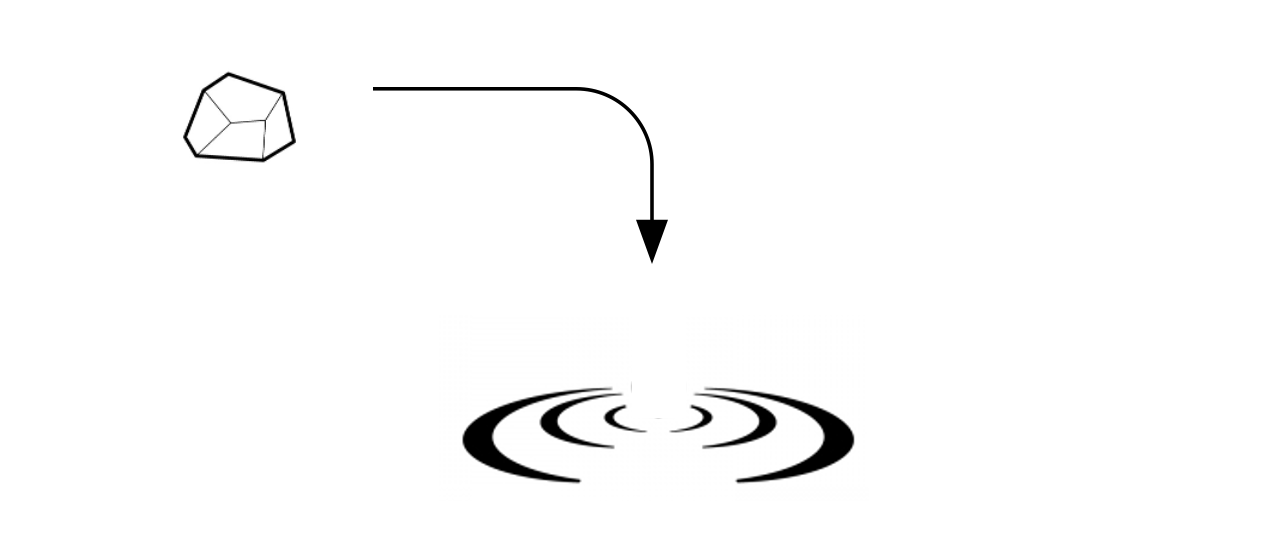
波紋は重さによって変わってきます。軽い石を投げ込めば小さな波紋が重い石を投げ込めば大きな波紋ができることでしょう。
そう考えると、波紋というものは石の情報を表しているものと考えることができると思います。言い換えると、石という入力情報が、容器の水(リザバー)によって、波紋に変換されたと考えることができるでしょう。
しかし、ただ波に変換されたわけではありません。
石を投げ込んだ後、波紋ができ、次第に波は小さくなり水面に消えていくことでしょう。波が生じ消えていくまでを、石を投げたことによる影響と考えれば、石の持つ情報は波という空間パターンが生じ消えていくまでの時空間パターンへと変換していることがわかります。
さらに続けて、また石を投げ込むと、また波紋ができますが、前に投げ込んだ波紋と合わさって、複雑な波ができることでしょう。
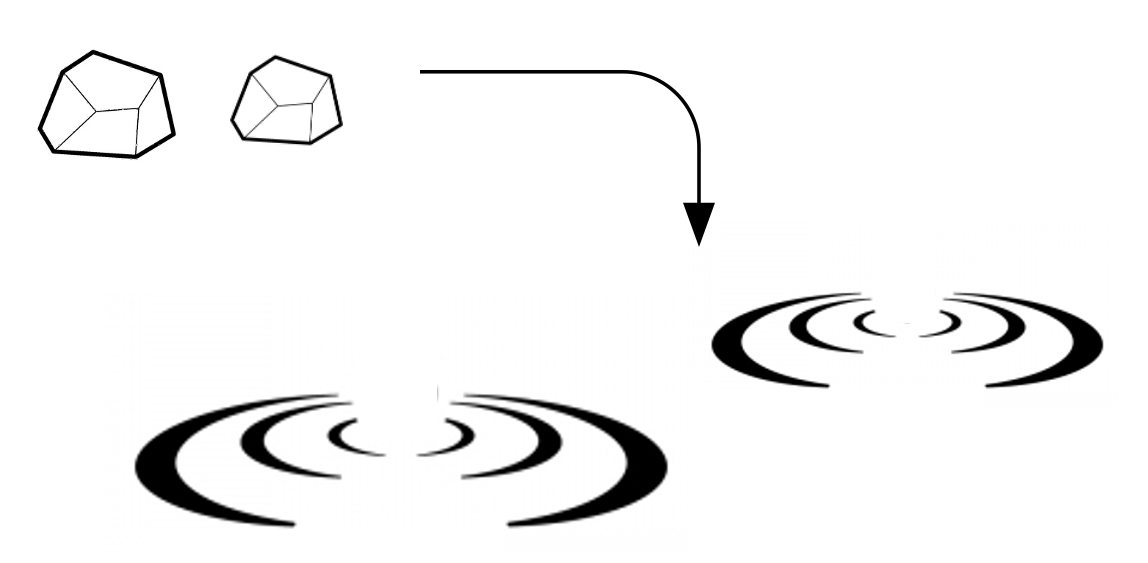
さて、先程波紋は石の情報を表していると言いましたが、この場合はどうでしょうか?
投げ込む石の2つのケースを考えてみましょう。
ケース1.
- 重い石を投げ込む
- 軽い石を投げ込む
ケース2.
- 軽い石を投げ込む
- 重い石を投げ込む
2つのケースでは波紋は異なってくることは容易に想像がつくでしょう。生じた波紋は、前に投げ込んだ石と、今投げ込んだ石の順番の情報を表しているものと考えることができます。波紋がそれまでに入力された石の影響を残すということは、過去の入力情報を保存しているということを意味します。
そう考えると、投げ込んだ石の列は時系列の入力は、蓄えられた水(リザバー)によって波紋という時空間パターンへと変換されています。ただ、変換されたわけではなく、過去の入力情報含んでいるというのが重要です。
ですから、この波紋を分析すれば、どのような順序で石を投げ込んだか、何番目に投げ込んだ石の重さはどうだったのかもわかるでしょう。ここで、この波紋をどのようにベクトル化するかですが、容器に蓄えられた水をビデオで上から撮影し、時間ごとの波のパターン画像をベクトルに変換すれば良いでしょう。そのベクトルを分析すれば、良いということです。
さて、時系列入力によって時空間パターンへ変換されたものを線形学習器に入力していきます。そのために線形学習器を説明しなければいけません。
線形学習器には大きく2つのタスクがあります
・線形分類
まず、線形分類について説明します。線形分類は、クラスが異なるデータ群の境界線を決定するものです。例えば、「芸能」「政治」のジャンルが異なる記事データがいくつかあった時、ジャンル分けするように境界線を決定します。境界線を決定すれば、記事データを線形分類器に入力すれば、どのジャンルかを出力します。線形分類は、データが二次元平面上にあるときは直線で境界線を決定します。ぐにゃぐにゃの曲線で境界線を決定することはできません。
・線形回帰
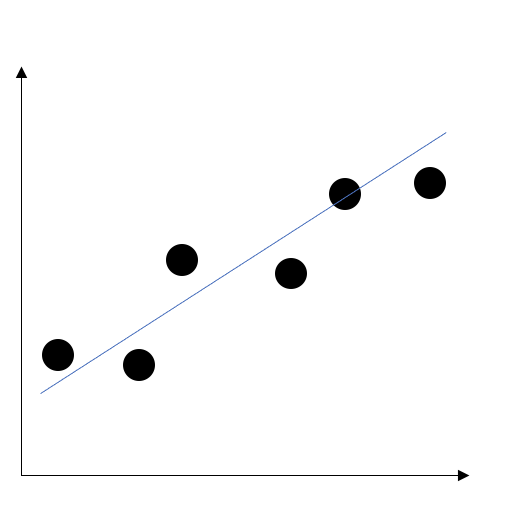
次に、線形回帰について説明します。線形回帰は、あるデータがあった時、近似するように直線を決定します。例えば、ばねはフックの法則に従っていて、ばねののびに比例して弾性力が変化します。この法則を実験で確かめたいときにばねの伸びと、その時の弾性力を計測する実験をしてデータを得たとしますが、だいたいノイズが含まれていてフックの法則通りの直線のようにはなりません。そこで線形回帰を利用することで近似しフックの法則に従っているか確かめることができます。
しかし、フックの法則のような直線的な法則ならば線形回帰を扱うことができますが、非線形なぐにゃぐにゃな曲線の法則があった場合、うまく近似することができません。
長い説明になってしまいましたが、線形分類も線形回帰も、非線形な分類や回帰ができないので深層学習のように高度な分類や回帰はできません。しかし、計算コストは低く、短時間で学習できるのが強みです。
さて、話を戻し、投げ込んだ石の列は時系列の入力は、蓄えられた水(リザバー)によって波紋という時空間パターンへと変換されました。その時空間パターンを線形学習器に入力します。今回の場合、石の系列を分類することを考えましょう。3個の石を順番に投げ込むとすると、「重い」と「軽い」の2通りあるので、8通り考えられます。この8個の系列を分類することを考えます。
なので系列ごとの時空間パターンと正解ラベル(例えば、0~7などのラベル)のセットを線形分類器に入力し学習させます。うまく学習することができていれば、「重い→軽い→軽い」の順番で投げ込めば、分類器が「重い→軽い→軽い」と入力したなと予測してくれます。
しかし、実は線形分類も線形回帰も、非線形な分類や回帰ができないので深層学習のように高度な分類や回帰はできません。それでも、リザバー計算では、線形学習器をあえて利用して、低コストで高速な学習を可能にしています。一体どのようにしてでしょうか。
簡単に言えば、
「リザバーによって入力データを線形分類したり回帰できるような形に変換している」
のです。
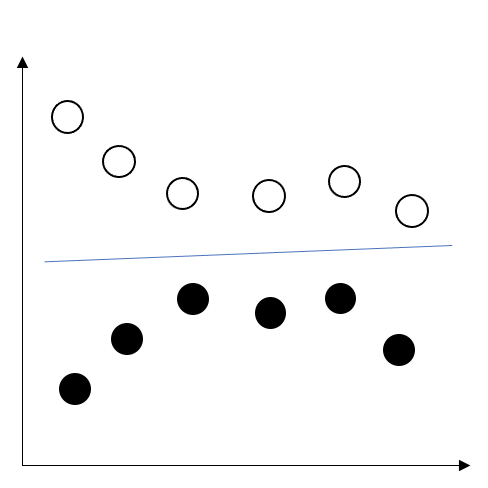
もう少し詳しくいうと、リザバーの役割は入力データを非線形変換し高次元特徴空間へと写像することです。
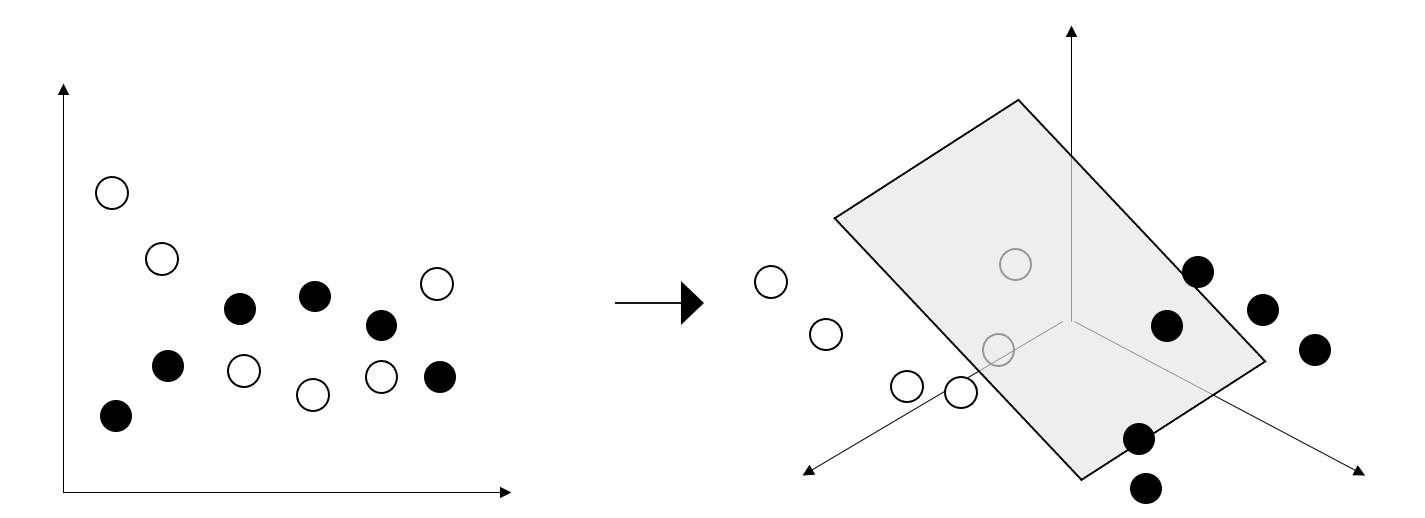
上の図のように、○と●の時系列があったとき、左の二次元平面上では直線では○と●で分類することはできません。しかし、右の三次元平面上に移すことで、平面で分類することが可能になります。今回は視覚的に説明するため、二次元と三次元で説明しましたが、実際は、もっと高次元な特徴空間に写像します。
容器に蓄えられた水は、非線形性を持っています。実際に波の重ね合わせは、振幅が非常に小さい時でしか成り立たないようです。なので水に石を投げ込むこと非線形な振る舞いをする波紋パターンができます。十分にリザバーとしての役割を果たしています。
さて、リザバーの役割について触れたので、ここで何を満たせばリザバーとして利用できるかをもう少し詳しく説明します。リザバーは以下の3つの特性を満たしていることが望ましいとされています。
・非線形性
リザバーは入力データを非線形変換するために、リザバーは非線形性が求められます。
・高次元性
リザバーは入力データを線形分類器に適用できるように高次元特徴空間へ写像することが求められます。
・短期記憶
リザバーは、時系列データを分類したり回帰するために過去の入力データを保存している必要があります。
「非線形性」「高次元性」「短期記憶」を満たしたものであれば、リザバーとしてなんでも利用できます。既に述べましたが、ソフトウェアでの実装だけでなく、容器の水やタコの足でも実装できます。
さて、以上で「時系列入力」「リザバー」「線形学習器」について順番に、蓄えられた水を例にして説明してきました。繰り返しになりますが、リザバー計算の流れは以下のようになっていましたね。
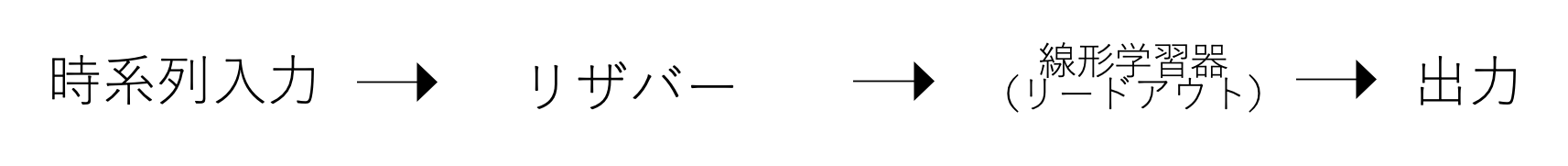
実際、リザバー計算は深層学習に比べて、学習するのは線形学習器だけですので非常に単純です。
深層学習の場合は、損失関数から出力側から入力側に向けて誤差逆伝播によって、ネットワークのパラメータを学習するコストがあります。しかし、リザバー計算ではそのようなことをする必要はなく入力を非線形変換し、計算時間のかからない単純な線形学習器に通して、出力するだけです。
ここで、リザバー計算のメリットをいくつかあげてみましょう。
・RNNのような同規模のディーブラーニングモデルよりも高速に学習できる
・高速学習なので、学習と検証のサイクルを伴うパラメータの調整を短時間で行うことができる
・計算資源と消費電力を抑えることができる
デメリットをあげてみましょう。
・学習パラメータが少ないので深層学習よりは表現能力が高くなく計算性能が少し低い。
以上を踏まえると、
リザバー計算は、エッジコンピューティング(データが生じるユーザの端末やセンサなどの近くで計算を行う方式)に向いていると言われています。
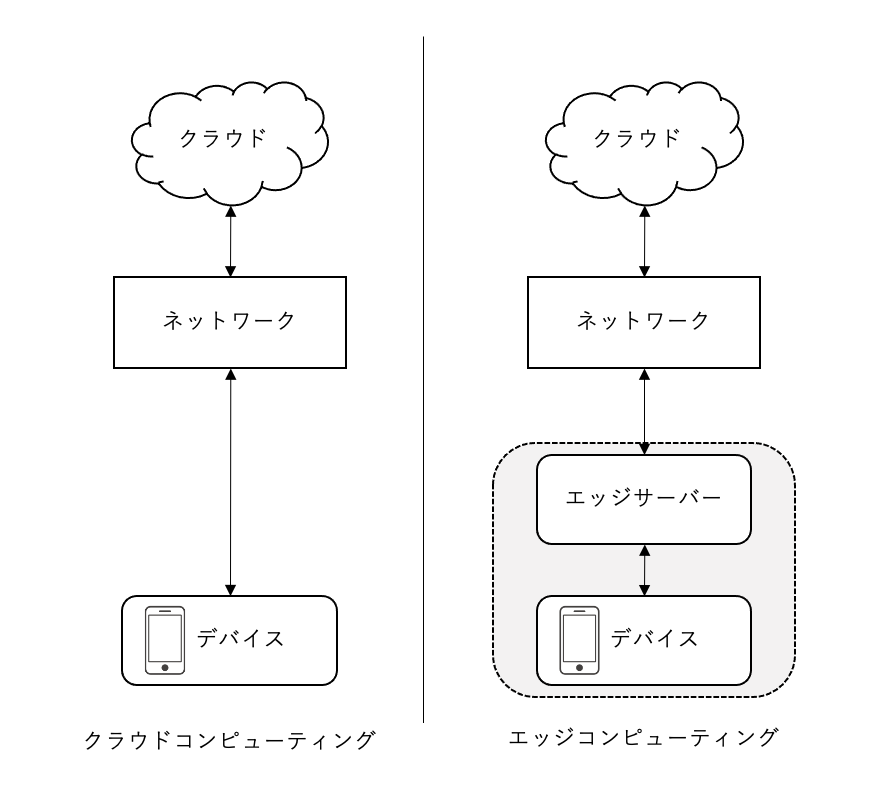
エッジ側では、大量の時系列データが生じるので、時系列データ処理に適した高速に学習できるリザバー計算は向いています。このような計算処理は、IoT社会で懸念されているデータ通信量の急増とデータトラフィックの集中を緩和し、情報の安全性の確保にもつながります。
一方でクラウド側では、時間をかけてたくさんの情報処理を扱うことができるので従来通り深層学習が向いています。
将来的にはクラウド側で深層学習とエッジ側でリザバー計算の使い分けが生じると考えられます。
ですが、まだリザバー計算は研究段階でほとんど実用化はされていない技術なので今後の研究で新しい用途が生まれてくると思っています。私は今後の革新的な技術の一つとして期待しています。
今回はリザバー計算の理論について説明しました。
実際に私はリザバー計算を実装し、かなり面白い結果が得られたので、実装編まで書きたかったのですが、実装の説明が長くなりそうでしたので今回は理論だけにとどめることにしました。
次回は「リザバー計算 実装編」の記事を書く予定ですので、よろしくお願いします。




