技研のまつけんです。
前回に引き続き、Officeドキュメントを自動編集したり自動生成したりしたいと思います。今回はPowerPoint文書に関数を「曲線」でプロットしてみます。
例えば、4周期分の正弦波をプロットすると以下のようになります:
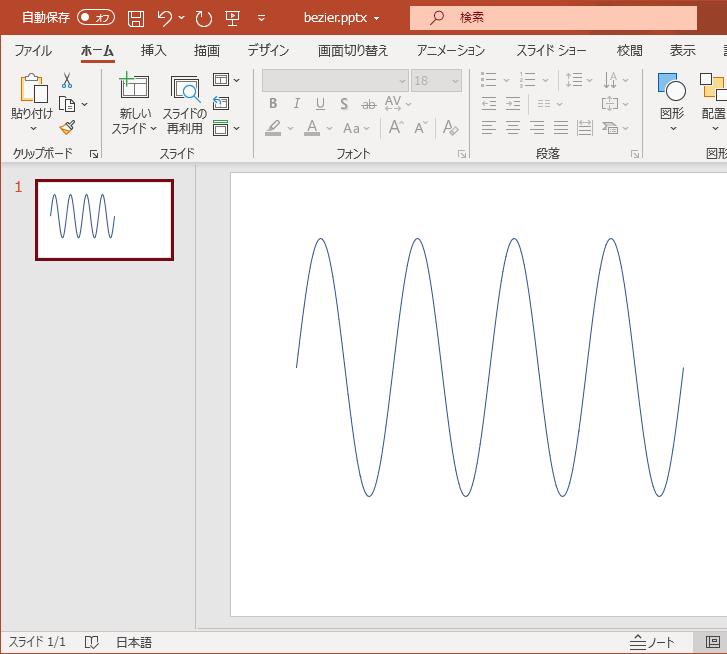
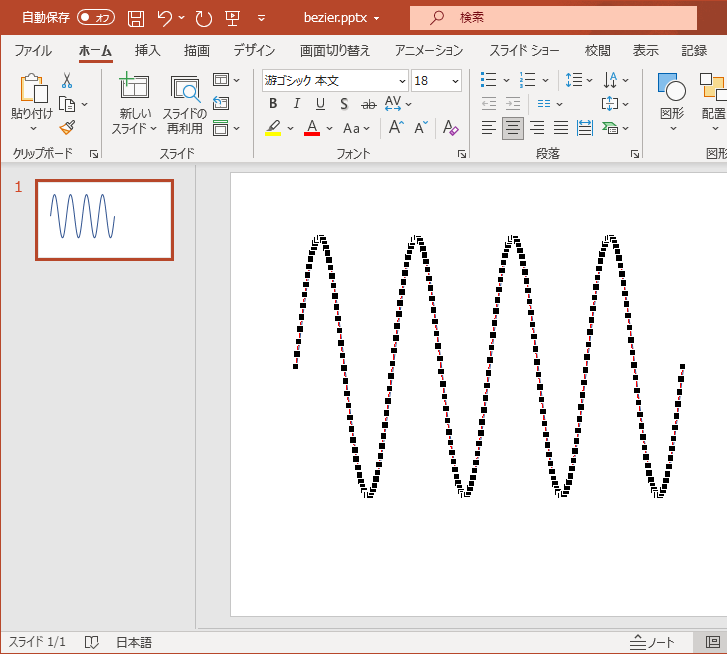
こちらは、256の点からなる「曲線」オブジェクトなので、右クリックして「頂点の編集」を選ぶと編集することが出来ます:
ExcelでプロットしたグラフをPowerPointに張り付けることも出来ますが、模式図を書きたいときには、枠や軸などを消す必要があり、バウンディングボックスも曲線に対して大きめになってしまったりと、少し不便です。また、Excelでプロットするには、関数を一旦CSVなどに保存するなどの手間も掛かります。その点、曲線だけを直接pptxファイルに吐き出すことが出来れば便利と思い、作成しました。
まずは、pptxファイルで「曲線」オブジェクトがどのように表現されているのか調べます。「頂点の編集」をすると頂点と一緒に腕のようなものが表示されるので、どうやらベジエ曲線のようです。
4つの点からなる適当な「曲線」を作成し、そのpptxファイルを前回の記事で紹介したunpack_pptx.shで展開してみます。「曲線」は「フリーフォーム」という名前で保存されているようです:
| <p:nvSpPr> |
| <p:cNvPr id="3" name="フリーフォーム: 図形 1"> |
| (略) |
| <a:off x="1000000" y="1000000"/> |
| <a:ext cx="1002506" cy="928687"/> |
| (略) |
| <a:pathLst> |
| <a:path w="1002506" h="928687"> |
| <a:moveTo> |
| <a:pt x="0" y="928687"/> |
| </a:moveTo> |
| <a:cubicBezTo> |
| <a:pt x="113109" y="457993"/> |
| <a:pt x="228601" y="332582"/> |
| <a:pt x="338138" y="290513"/> |
| </a:cubicBezTo> |
| <a:cubicBezTo> |
| <a:pt x="447675" y="248444"/> |
| <a:pt x="545306" y="676275"/> |
| <a:pt x="657225" y="676275"/> |
| </a:cubicBezTo> |
| <a:cubicBezTo> |
| <a:pt x="769144" y="676275"/> |
| <a:pt x="904875" y="130175"/> |
| <a:pt x="1002506" y="0"/> |
| </a:cubicBezTo> |
| </a:path> |
| </a:pathLst> |
| </a:custGeom> |
| <a:noFill/> |
| </p:spPr> |
数値が羅列されていますが、最初のx、y、cx、cyはオブジェクトのバウンディングボックスのようです。次のw、hは、cx、cyと一致しています。そのあとの、moveToとcubicBezToがベジエ曲線のpathを表現していると推測されます。これはPostScriptのベジエ曲線の表現
| newpath |
| x0 y0 moveto |
| x1 y1 x2 y2 x3 y3 curveto |
| x4 y4 x5 y5 x6 y6 curveto |
| x7 y7 x8 y8 x9 y9 curveto |
によく似ています (なお、PDFではmovetoはm、curvetoはcで表します)。また、moveToとcubicBezToの中で使う座標は、バウンディングボックス内の相対座標のようです。
PostScriptでは、この後ろに
| x10 y10 x11 y11 x12 y12 curveto |
| x13 y13 x14 y14 x15 y15 curveto |
のように新たなcurvetoを追加すれば曲線を延長できますが、pptxファイルについても、テキストエディタで <a:cubicBezTo>~</a:cubicBezTo> を追加してみたところ、同じように延長できることがわかりました。
前回はbashスクリプトでしたが、今回はPythonで作成したいと思います。NumPyを使えば、sin、cosなどが手軽に利用できますし、最終的にPythonで行った実験の結果をPowerPointで発表するという連携が出来ると便利だからです。
途中に任意の数字などを入れた長いXMLを生成しなければなりません。また、途中に多数のダブルクオートも含まれますし、スペースや改行が挟まるとPowerPointで開くときにエラーになることもあります。
| s += '''<a:off x="%d" y="%d" />''' % (x, y) |
| s += '''<a:ext cx="%d" cy="%d" />''' % (cx, cy) |
など、色々な書き方を検討した結果、以下のような方針で記述することにしました。
まず、
| s = \ |
| '''<p:spPr>''' + \ |
| '''<a:xfrm>''' + \ |
| '''<a:off x="***X***" y="***Y***"/>''' + \ |
| '''<a:ext cx="***CX***" cy="***CY***"/>''' + \ |
| '''</a:xfrm>''' + \ |
| (略) |
| '''</p:spPr>''' + \ |
のように座標などの数値を入れるべき部分を ***変数名*** に置き換えた文字列を作ります。そして、それぞれの値をdictで保存しておき、置換します:
| dic = { |
| 'X': 1000000, |
| 'Y': 1000000, |
| 'CX': 1002506, |
| 'CY': 928687, |
| } |
| for key in dic: |
| s = s.replace('***' + key + '***', str(dic[key])) |
このようにすれば、Pythonソースコード上で、インデントや改行を保ったまま編集できますし、置換する直前に print(s) することで、どこにどの変数が入るのか確認できます。また、複数回の置換を行うことでテキストを階層化することも可能です。
以下の通りです (一部、省略しています):
| import numpy as np |
| from numpy import pi as PI, linspace, sin, cos, tan, log10, sqrt, where |
| X = 1000000 |
| Y = 1000000 |
| W = 6000000 |
| H = 4000000 |
| omega = 2 * PI * 4 |
| xlim = (0, 1) |
| ylim = None |
| pts = 256 |
| xs = linspace(*xlim, pts) |
| ys = sin(omega * xs) |
| #tlim = (0, 1) |
| #ts = linspace(*tlim, pts) |
| #xs = ts * cos(omega * ts) |
| #ys = ts * sin(omega * ts) |
| s = \ |
| '''<?xml version="1.0" encoding="UTF-8" standalone="yes"?>''' + '\n' + \ |
| '''<p:sld xmlns:a="http://schemas.openxmlformats.org/drawingml/2006/main" xmlns:r="http://schemas.openxmlformats.org/officeDocument/2006/relationships" xmlns:p="http://schemas.openxmlformats.org/presentationml/2006/main">''' + \ |
| '''<p:cSld>''' + \ |
| '''<p:spTree>''' + \ |
| (略) |
| '''<p:cNvPr id="3" name="フリーフォーム: 図形 1">''' + \ |
| (略) |
| '''</p:cNvPr>''' + \ |
| '''<p:cNvSpPr/>''' + \ |
| '''<p:nvPr/>''' + \ |
| '''</p:nvSpPr>''' + \ |
| '''<p:spPr>''' + \ |
| '''<a:xfrm>''' + \ |
| '''<a:off x="***X***" y="***Y***"/>''' + \ |
| '''<a:ext cx="***CX***" cy="***CY***"/>''' + \ |
| '''</a:xfrm>''' + \ |
| '''<a:custGeom>''' + \ |
| (略) |
| '''<a:rect l="l" t="t" r="r" b="b"/>''' + \ |
| '''<a:pathLst>''' + \ |
| '''<a:path w="***CX***" h="***CY***">''' + \ |
| '''***PATH***''' + \ |
| '''</a:path>''' + \ |
| '''</a:pathLst>''' + \ |
| '''</a:custGeom>''' + \ |
| '''<a:noFill/>''' + \ |
| '''</p:spPr>''' + \ |
| '''<p:style>''' + \ |
| (略) |
| '''</p:style>''' + \ |
| '''<p:txBody>''' + \ |
| (略) |
| '''</p:txBody>''' + \ |
| '''</p:sp>''' + \ |
| '''</p:spTree>''' + \ |
| '''<p:extLst>''' + \ |
| (略) |
| '''</p:extLst>''' + \ |
| '''</p:cSld>''' + \ |
| '''<p:clrMapOvr>''' + \ |
| '''<a:masterClrMapping/>''' + \ |
| '''</p:clrMapOvr>''' + \ |
| '''</p:sld>''' |
| path = \ |
| '''<a:moveTo>''' + \ |
| '''<a:pt x="***X0***" y="***Y0***"/>''' + \ |
| '''</a:moveTo>''' |
| n = 1 |
| for _ in range(pts - 1): |
| path += \ |
| '''<a:cubicBezTo>''' |
| for _ in range(3): |
| path += \ |
| '''<a:pt x="***X%d***" y="***Y%d***"/>''' % (n, n) |
| n += 1 |
| path += \ |
| '''</a:cubicBezTo>''' |
| dic = { |
| 'X': X, |
| 'Y': Y, |
| 'CX': W, |
| 'CY': H, |
| 'PATH': path, |
| } |
| if ylim is not None: |
| ys[where(ys < ylim[0])] = ylim[0] |
| ys[where(ys > ylim[1])] = ylim[1] |
| xs -= np.min(xs) |
| xs /= np.max(xs) |
| ys -= np.min(ys) |
| ys /= np.max(ys) |
| for i, (x, y) in enumerate(zip(xs, ys)): |
| x_ = round( x * W) |
| y_ = round(-y * H + H) |
| i *= 3 |
| dic['X' + str(i - 1)] = \ |
| dic['X' + str(i )] = \ |
| dic['X' + str(i + 1)] = x_ |
| dic['Y' + str(i - 1)] = \ |
| dic['Y' + str(i )] = \ |
| dic['Y' + str(i + 1)] = y_ |
| for key in dic: |
| s = s.replace('***' + key + '***', str(dic[key])) |
省略されている部分は、「適当な曲線を保存したpptx」からそのまま持ってきたものです。先程、言及した「テキストの階層化」は ***PATH*** の部分です。 for _ in range(pts - 1) のループ内で、
| <a:moveTo> <a:pt x="***X0***" y="***Y0***"/> </a:moveTo> |
| <a:cubicBezTo> <a:pt x="***X1***" y="***Y1***"/> <a:pt x="***X2***" y="***Y2***"/> <a:pt x="***X3***" y="***Y3***"/> </a:cubicBezTo> |
| <a:cubicBezTo> <a:pt x="***X4***" y="***Y4***"/> <a:pt x="***X5***" y="***Y5***"/> <a:pt x="***X6***" y="***Y6***"/> </a:cubicBezTo> |
| <a:cubicBezTo> <a:pt x="***X7***" y="***Y7***"/> <a:pt x="***X8***" y="***Y8***"/> <a:pt x="***X9***" y="***Y9***"/> </a:cubicBezTo> |
| (略) |
| <a:cubicBezTo> <a:pt x="***X760***" y="***Y760***"/> <a:pt x="***X761***" y="***Y761***"/> <a:pt x="***X762***" y="***Y762***"/> </a:cubicBezTo> |
| <a:cubicBezTo> <a:pt x="***X763***" y="***Y763***"/> <a:pt x="***X764***" y="***Y764***"/> <a:pt x="***X765***" y="***Y765***"/> </a:cubicBezTo> |
のような文字列 (実際にはスペースや改行は無し) を生成しておき、dicに 'PATH': path を登録することで置換します。その後、X0~X765、Y0~Y765が for i, y in enumerate(ys) のループで登録された座標で置換されます。
周期の数は、角周波数omegaとxの範囲xlimで指定します。上記の組み合わせでは、「4ヘルツの波を1秒間だけプロットする」という内容の設定になっているので4周期だけプロットされます。今回はx∈[0, 1]でプロットしたかったので、linspaceを使ってのリストxsを生成していますが、x∈[0, 1)にしたい場合は、np.arangeを使うか、 xs = np.array(range(pts)) / pts とします (個人的にはlinspaceとarangeの引数の順序を忘れがちなので後者を使います)。
コメントアウトされいている部分を有効にすると、媒介変数tによる渦巻のプロットになります (sinとcosでハートマークを描く式なども知られていますので、試してみては如何でしょうか?)。
少なくとも2点あります。
1つ目は、ベジエ曲線を使っているのに、連続する3つの点 (Adobe Illustrator用語で言うところの各アンカーポイントの両側の制御点) に同じ座標を指定しているので、点と点の間が直線になってしまっていることです。これについては、点の密度を細かくすることで、直線であることを見えにくくすれば解決できます。解決策としては、各点をスプライン曲線で接続しているものとして、それをベジエ曲線に変換するという方法が考えられます。
2つ目は、tanのように無限大に発散してしまう関数を複数周期プロットする場合に備えて、ylimを指定できるようにしていますが、ylimの範囲外の値になる部分が水平な直線になってしまう点です。これについては、テキストエディタでの実験では
| <a:moveTo> ~ </a:moveTo> |
| <a:cubicBezTo> ~ </a:cubicBezTo> |
| <a:cubicBezTo> ~ </a:cubicBezTo> |
| <a:cubicBezTo> ~ </a:cubicBezTo> |
| <a:moveTo> ~ </a:moveTo> |
| <a:cubicBezTo> ~ </a:cubicBezTo> |
| <a:cubicBezTo> ~ </a:cubicBezTo> |
| <a:cubicBezTo> ~ </a:cubicBezTo> |
のように記述すれば、途切れた2本の曲線が描けることが確認できています。ただし、 <a:pathLst>~</a:pathLst> の中に <a:path>~</a:path> が入る構造になっているので、 <a:path>~</a:path> を追加するのが正しいのかも知れません。
前回の記事で紹介したpack_pptx.shを少し改良しました:
| # pack_pptx.sh |
| # ディレクトリからPowerPointファイルを生成 |
| TGT=`basename "$1" .pptx` |
| find "$TGT" -iname "*.xml" | while read FILE |
| do |
| sed -e 's#^ \+##' \ |
| -e 's# />#/>#g' -i "$FILE" |
| sed -z 's#[\r\n]##g' -i "$FILE" |
| sed -e 's#\([^^]\)<#\1\r\n<#' -i "$FILE" |
| done |
| rm -f "$TGT".pptx |
| ( cd "$TGT" ; zip -r ../"$TGT".pptx * ) |
find ~ do ~ doneを追加することで、整形済みのXMLファイルを元に戻してからzip圧縮するようにしました。これにより、見やすい形で編集した結果をそのままpptxファイルに戻すことが出来ます。
少し調べてみたところ、.NET Frameworkを利用すると、クリップボードに直接、Windows Meta形式で、ベジエ曲線を書き込むことも出来そうでした。C++やC#で実験した結果をPowerPointに貼りつけたい場合は、その方が相性が良いかも知れません。




