こんにちは!クレスコ・デジタルテクノロジーズの前山です。
私は、元々数理に興味があり、数理に基づいている暗号化方式の勉強をしていました。暗号化方式というと、情報処理技術者試験にも出題されていますし、たくさんのHPでも共通鍵暗号方式や公開鍵暗号方式の仕組みについて書かれているので、ご存じの方も多いかと思います。
今回は、数理という観点で、公開鍵暗号方式の裏側をみなさんにお伝えしたいと思います。
- 公開鍵暗号って?
- 数理の世界
- 検証してみた
- おわりに
まずは、簡単な暗号方式であるシーザー暗号方式について考えてみましょう。
暗号化したい元の文(平文と言います)と暗号鍵から、他の人が見てもぱっとは分からない「暗号文」を生成します。暗号文を生成することを「暗号化」と呼びます。暗号化をする時の方式で、そのキーとなる数字を暗号鍵と呼びます。
シーザー暗号の場合は、アルファベットを○文字分だけずらす、と言う方式で暗号化します(例:「CRESCO」をアルファベット「3」文字分だけ、後ろにずらして「FUHVFR」にする、など)。
暗号文を、受け取った人が元の平文に戻す作業を 復号、もしくは復号化と呼びます(例:「FUHVFR」をアルファベット「3」文字分だけ、前にずらして「CRESCO」にする、など)。
この場合、暗号化する時の暗号方式と復号化する時の復号方式が同じロジックとなりますね。この状態「○文字分だけ操作する」と言う○の数字の部分と「進む」「戻す」と言う操作が暗号化/復号化に使用される「鍵」と呼ばれます。
この暗号化と復号化での鍵が同じであるものを、共通鍵暗号方式と呼びます。
ただこれには問題があります。そもそも暗号の役割とは、他の人に知られずに特定の人に秘密の内容を送るためのものなのですが、どうしても伝達の途中で悪意ある第三者が介入し暗号鍵と暗号文が傍受されるリスクがあるのです。仮にそうなった場合、秘密にしたい元の文章がバレてしまいます。
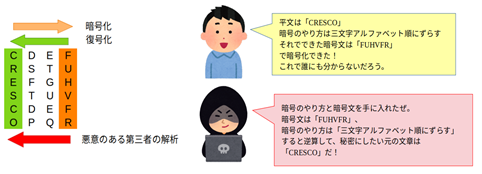
また、別の問題もあります。そもそも暗号文を受け取る相手は、暗号文を受け取っても、戻す方式(復号化・復号鍵)を知らなければ、平文に戻すことができません。しかし、事前に暗号化・復号化方式を個別に取り決めておくのは大変です。
そこで公開鍵暗号方式の登場です。
共通鍵暗号方式では、暗号化する際の鍵と、復号化する際の鍵については、同じものを使用していました。公開鍵暗号方式では、暗号化専用の鍵・復号化専用の鍵として別の鍵を用意するのです。そして暗号化する専用の鍵はなんと公開してしまいます(なので、「公開」鍵暗号方式と言うんですね)。
本来であれば、暗号鍵を公開なんてしたら、あっという間に悪意のある第三者に解析されて、元の平文が解ってしまったでしょう。
しかし、この公開されている暗号鍵は、割り算の余りを使用するなどして、平文を求める為の逆算が大変困難になっており、暗号文と暗号鍵を手に入れても平文が割り出せません。
そして、復号鍵は秘密にしておきます。この復号鍵は計算で求めることも理論上可能なのですが、計算量が膨大になりすぎて、現実的な解析が非常に困難です。


数学の世界で、循環する数の世界のことを「法」と言います。
例えば、本来、1→2→3→4→5→・・・と進む数の世界は、3を法とする数でいえば、1→2→3→1→2→3→1→2→・・・と循環する数の数え方を指します。
一番身近なのは時計ですね。例えば今が昼の12時だったとして、13時間進むと夜の1時になります。どれだけ時間が進もうとも、ある一定の尺度範囲の数え方の中でその数の取り決めをしてしまおうと言うのが数学における「法」の世界です。
時計については、数学的には「12を法とする世界で考える」と言います。
これは割り算で割った後のあまりと言う解説でよく説明されます。
上記の例で言えば、13時間を12時間の法で割ると、1があまり、循環の基点から1進んだことを示しています。
さて、ここからかなり話は飛躍しますが、数学の研究によって、いろんな数をこねくりまわすと、数には面白い性質があることが分かってきました。
結論から言えば、素数pと素数qでの積p×qを用意し、このp×qを法とする世界では、(p-1とq-1の最小公倍数×n)+1乗の時に、ランダムに指定した値が元の数に戻ると言うのです!
文章だと分かりにくいと思いますので、下記の表をざっくり見て下さい。
表1 :べき乗とあまりの対応表
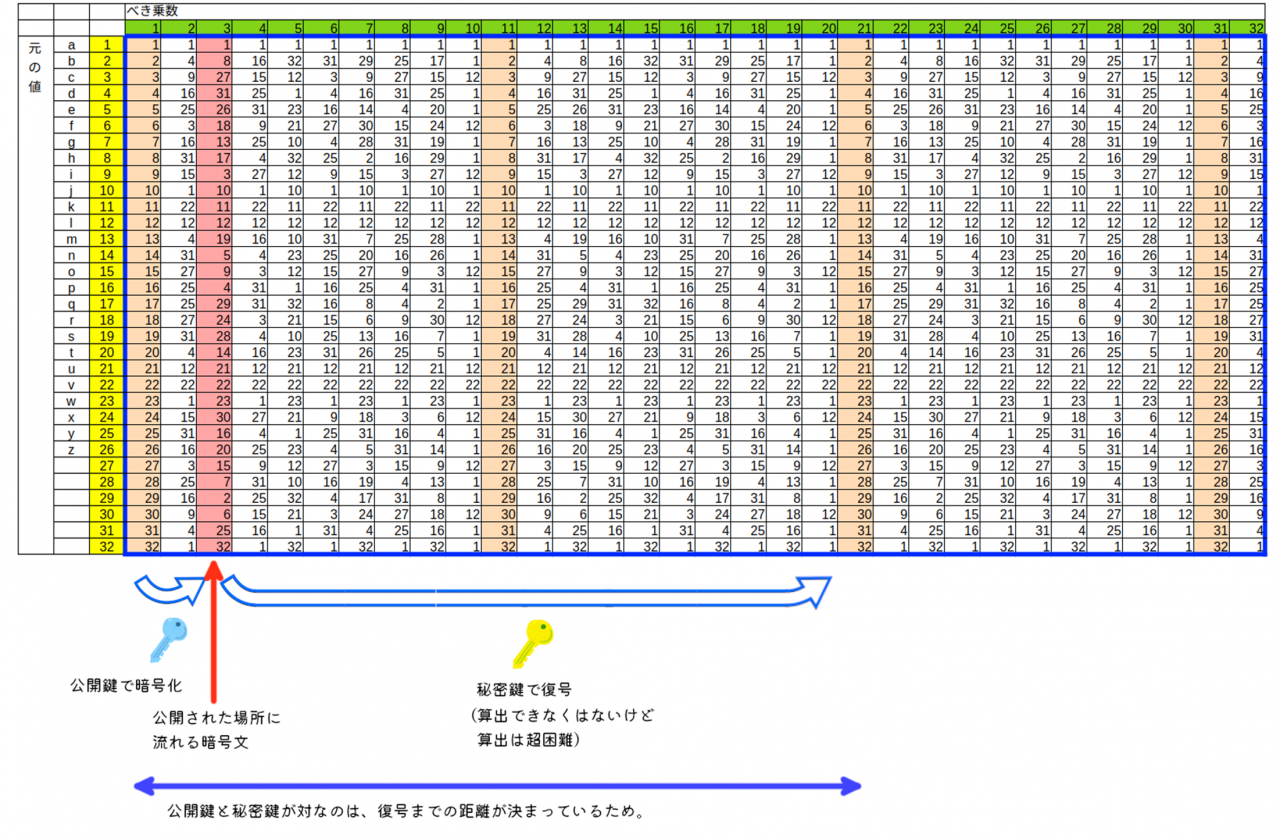
ここではp=3、q=11でのp×q=33を法とする世界で、アルファベットを縦に並べて、黄色の列の01〜26に対応させます。その数を横に並べた緑色の行の数でべき乗し、得た値を法の数である33で割り、その余りを青太枠の中に記載しています。
これは元の数字(黄色の列)をべき乗して割り算した結果、余りはこの数字になりますよ、という表なのですが、よく見ると、薄オレンジの列の数字は綺麗に元の数字に戻っていますね。
素数pと素数qでの積を法とする世界の場合、(p-1とq-1の最小公倍数×n)+1乗(すなわち薄オレンジの列)の時に 元の数字に戻るのです。
また、図解雑学 暗号理論によれば、この表のもう一つの性質として、特定の乗算での結果(ここでは表1の赤色の列の値)は、その結果を基に更に計算を進めていくと、この「元の数字(薄オレンジの列)に戻る」性質もあると言うのです。
上記の表に従って言い換えると、元の数字(黄色の列)を緑色の行の数字でべき乗(今回は3を使用)し、法である33で割った余り(赤色の列)を、更に薄オレンジの列に辿り着くまでの数でべき乗(今回は17を使用)し、それを法の33で割ると薄オレンジの列の数に戻るのです!
試しに、「CRESCO」の文字で確認してみましょう。
(1)まずアルファベットを数字に置き換えます。
C→03、R→18、E→05、S→19、C→03、0→15
(2)これを3でべき乗し、33で割り、その余りを求めます。
C:= 27/ 33 = 0 あまり27 → 27
R:= 5832 / 33 = 176 あまり24 → 24
E:=125 / 33 = 3 あまり26 → 26
S:=6859 / 33 = 207 あまり28 → 28
C:=27/ 33 = 0 あまり27 → 27
O:=3375 / 33 = 102 あまり 9 → 9
この計算結果は27 24 26 28 27 09 となります。
これが暗号化です。
(3)更にそれぞれの数を17でべき乗し、33で割り、その余りを求め、復号化します。
27:= 2153693963075557766310747 / 33
= 65263453426532053524568 あまり3
→ 3 →「C」に復号
24:= 290797794982682557415424 / 33
= 8812054393414622951982 あまり18
→ 18 →「R」に復号
26:= 1133827315385150725554176 / 33
= 34358403496519718956187 あまり 5
→ 5 →「E」に復号
28:= 3996561798506898509529088 / 33
= 121107933288087833622093 あまり 19
→ 19 →「S」に復号
27:= 2153693963075557766310747 / 33
= 65263453426532053524568 あまり3
→ 3 →「C」に復号
9:= 16677181699666569 / 33
= 505369142414138 あまり15
→ 15 →「O」に復号
と言うことで無事「CRESCO」の文字を暗号化でき、そして復号化できました。
(尚、上記のような桁数でもまだまだ小さい数です。本来であればもっと大きな数になります。)
今回は、数理という観点で解説を進めましたがいかがでしたか?
実際に計算をすることで、暗号化、復号化の仕組みが少し見えたのではないでしょうか。
普段こうした計算を意識することはありませんが、上記の計算が実際に行われていることによって、情報の安全が守られています。「こういう仕組みで安全なんだ」と理解頂ければ、書き手としてこの上なく嬉しく思います。
・参考書籍:伊藤 正史 (著)「図解雑学 暗号理論」ナツメ社
・計算に使用したコマンド:Linux bc




