この記事は『CRESCO Advent Calendar 2022』９日目の記事です。

 

技研のまつけんです。

説明可能AIについての研究をしています。元々の専門はFIRフィルタなので、学習済みCNN (convolutional neural network) モデルのフィルタ係数 (インパルス応答) を覗いたり、書き換えたりして、モデルの特性を探るということをやりたいと考えています。

それと関連して、以前からやってみたかった実験をやってみることにしました。それは、

  1. Conv2Dだけしかないモデルを構築すると、GPUでFIRフィルタを実行できるのか？ / CPUより高速なのか？
  2. 一般的なCNNのモデルの1層目に前処理FIRフィルタを入れることで前処理をモデルに含めることが出来るのか？ / 学習や推論は高速化できるのか？

です。

学習前に前処理として画像にFIRフィルタを掛けたりすることは、ありますよね。前処理はCPUで行うのが一般的だと思いますが、FIRフィルタはMAC演算が多いのでCPUではなくGPUで実行した方が高速に実行できそうです。それぞれの実験の結果は、

  1. 出来る / CPUとGPUのどちらが高速かは環境による
  2. 出来る / 学習の速度は前処理を行う方式による。推論の速度も環境による

でした。

実験環境

技研には、機械学習サーバが3台あり、その環境は以下の通りです:

環境1 環境2 環境3
CPU i7-8700K/3.70GHz i9-9900KF/3.60GHz i9-10980XE/3.00GHz
Main RAM (GB) 64 64 80
GPU GeForce GTX 3090 Ti GeForce RTX 2080 Ti GeForce GTX 3090 Ti
GPU RAM (MiB) 24,356 11,016 24,356
OS Ubuntu Linux Server 20.04 LTS
Software/Library Python 3.10 + TensorFlow 2.9.1 + CUDA Toolkit 11.7.0

今回は、環境1と2を使用しました。

オーソドックスなテストプログラム

例えば、CIFAR-10に適当なフィルタを掛けて学習し、推論する場合、以下のような処理となります (np.arrayは長い上にタイプミスしやすいので、naで記述できるようにしています):

import cv2
import numpy as np ; na = np.array
from keras.layers import Input, Activation, Conv2D, Dense, MaxPooling2D
from keras.models import Sequential
from keras.datasets import cifar10
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
HEI, WID = X_train.shape[1 : 3]
N_CLASSES = len(set(y_train.flatten()))
model = Sequential()
model.add(Input((HEI, WID, 3)))
model.add(Conv2D(32, (3, 3), activation='relu'))
model.add(MaxPooling2D((2, 2)))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D((2, 2)))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(N_CLASSES, activation='softmax'))
model.summary()
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
X_train = na([filter(img) for img in X_train])
model.fit(X_train / 255., y_train, epochs=10)
X_test = na([filter(img) for img in X_test ])
y_train_pred = np.argmax(model.predict(X_train / 255.), axis=1)
y_test_pred = np.argmax(model.predict(X_test / 255.), axis=1)

filter()は例えば、アンシャープマスクなどが有り得ます:

def make_sharp_kernel(k, shape):
N = np.prod(shape)
kernel = np.full(shape, -k / N)
centre = (na(shape) / 2).astype('i')
kernel[centre[0], centre[1]] = 1 + (N - 1) * k / N
return kernel
KERNEL_SIZE = (5, 5)
kernel = make_sharp_kernel(1, KERNEL_SIZE)
def filter(img, kernel):
return cv2.filter2D(img, -1, kernel)

アンシャープマスクの実装はこちらを参考にしています。アンシャープマスクを使った場合、10エポックでテストデータに対して、71～72%程度の正答率のモデルが出来ますが、使わなかった場合、つまり、

X_train = na([filter(img) for img in X_train])

と

X_test  = na([filter(img) for img in X_test ])

をコメントアウトした場合は、同64～67%程度となります。

準備運動: model.predict()でFIRフィルタリングしてみる

手始めに実験として、画像をフィルタリングするだけのモデルを作ってみます。まずは、InputとConv2Dだけしかないsequentialモデルを作ります:

model = Sequential()
model.add(Input((HEI, WID, 3)))
model.add(Conv2D(3, KERNEL_SIZE, padding='same'))

Conv2Dの最初の引数の3は、プレイン（チャネル）数（カラーならRGB、または、BGRの3プレイン）に由来します。学習/推論対象の画像がモノクロの場合は

model.add(Input((HEI, WID)))
model.add(Conv2D(1, KERNEL_SIZE, padding='same'))

となります (今回は実験していません)。

中身を表示:

model.summary()
print('# of Layers:', len(model.layers))
for layer in model.layers:
w = layer.get_weights()
print('Shapes:', w[0].shape, w[1].shape)
print(w)

させてみると、フィルタ係数 (インパルス応答) が乱数で初期化されていることがわかります:

Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 32, 32, 3) 228
=================================================================
Total params: 228
Trainable params: 228
Non-trainable params: 0
_________________________________________________________________
# of Layers: 1
Shapes: (5, 5, 3, 3) (3,)
[array([[[[-0.03206667, 0.08217172, -0.09534836],
[-0.14401308, -0.0009079 , -0.0059247 ],
[-0.06281738, -0.09222265, -0.00077529]],
　　　　　　　　（中略）
[[ 0.07242851, 0.11345352, 0.19228567],
[-0.1687601 , 0.09903173, -0.01579022],
[ 0.03920388, 0.03952417, -0.03529873]]]], dtype=float32), array([0., 0., 0.], dtype=float32)]

フィルタ係数は、get_weights()で取り出し、編集して、set_weights()で書き込みます。

w = model.layers[0].get_weights()
w[0] = （フィルタ係数）
w[1][:] = 0
model.layers[0].set_weights(w)

という感じです。w[0]がフィルタ係数、w[1]はバイアスなので、w[1]はすべて0にセットします。まずは、実験なので、簡単なフィルタ係数を用意します:

zeros = np.zeros(KERNEL_SIZE)
delta = zeros.copy() ; delta[int(KERNEL_SIZE[0] / 2), int(KERNEL_SIZE[1] / 2)] = 1
movave = np.full(KERNEL_SIZE, 1 / np.prod(KERNEL_SIZE))
dilate = np.ones(KERNEL_SIZE)
hordil = zeros.copy() ; hordil[int(KERNEL_SIZE[0] / 2), :] = 1

上から順に、何も出力しない、入力をそのまま出力 (クロネッカーのデルタ)、移動平均、膨張、水平方向にのみ膨張、です。カラー画像が対象の場合、以下のようにすることで、各プレインに対して膨張させることを記述します。変数名のirsはimpulse responsesの略です。

irs = na([[dilate, zeros , zeros ],
[zeros , dilate, zeros ],
[zeros , zeros , dilate]])

これをw[0]に代入するのですが、次元の順序を入れ替える必要があるので、np.transpose()で入れ替えます:

w = model.layers[0].get_weights()
w[0] = np.transpose(irs, (2, 3, 1, 0))
w[1][:] = 0
model.layers[0].set_weights(w)

準備はこれだけです。実際に中央1ピクセルだけが白で、残りが黒である画像を生成して、それに対して実行してみましょう。

imgs = np.zeros((1, HEI, WID, 3))
imgs[0][int(HEI / 2), int(WID / 2)] = 1
filterd_imgs = model.predict(imgs)
plt.imshow(imgs[0]) ; plt.show()
plt.imshow(filterd_imgs[0]) ; plt.show()

1ピクセル四方の点が5ピクセル四方に膨張していることがわかります:

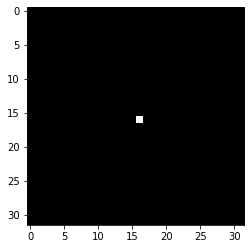
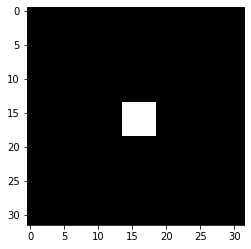
プレイン毎に異なる処理をすることも出来ます。こちらは、青に対しては膨張、緑に対しては水平に膨張、赤に対しては何もしない、という例です。

irs = na([[dilate, zeros , zeros],
[zeros , hordil, zeros],
[zeros , zeros , delta]])

アンシャープマスクを掛けてみる

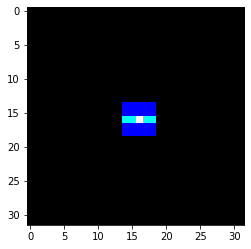
実際に5ｘ5のアンシャープマスクを実行してみます。

kernel = make_sharp_kernel(5, KERNEL_SIZE)
irs = na([[kernel, zeros , zeros ],
[zeros , kernel, zeros ],
[zeros , zeros , kernel]])
w = model.layers[0].get_weights()
w[0] = np.transpose(irs, (2, 3, 1, 0))
w[1][:] = 0
model.layers[0].set_weights(w)
imgs = np.full((1, HEI, WID, 3), .4)
imgs[0][int(HEI / 2), int(WID / 2)] = .6
filterd_imgs = model.predict(imgs)
plt.imshow(imgs[0]) ; plt.show()
plt.imshow(filterd_imgs[0][:, :, :: -1]) ; plt.show()

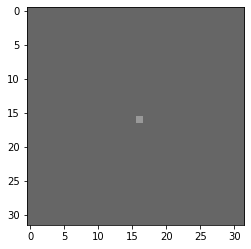
続いて、CPUでも処理してみます。

filterd_imgs_cpu = na([filter(img) for img in imgs])
plt.imshow(filterd_imgs_cpu[0][:, :, :: -1]) ; plt.show()

過渡応答 (端の部分) 以外は同じように見えます。実際に過渡応答を除いて比較:

diff = filterd_imgs_cpu[:, 2 : -2, 2 : -2] - filterd_imgs[:, 2 : -2, 2 : -2]
'%f %f' % (np.max(diff), np.min(diff))

してみると、誤差の範囲で一致していることが確認できました:

'0.000000 -0.000001'

なお、このアンシャープマスクを実データ (CIFAR-10のX_train[0]) に対して適用すると、

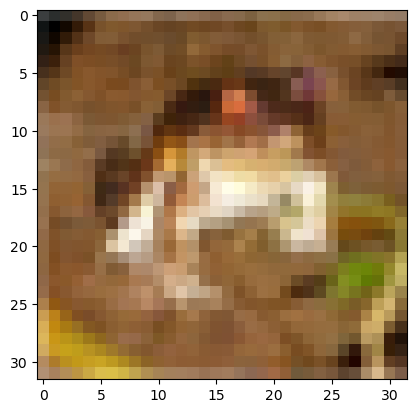
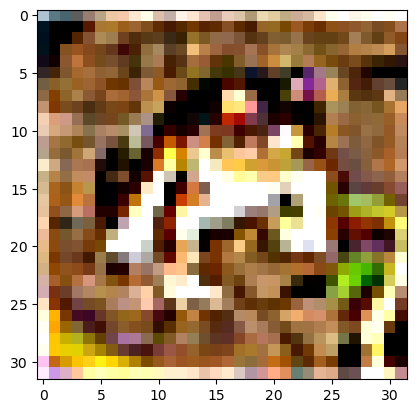
のようになります。

実行時間の測定と比較

実行時間をCPUとGPUで比較してみます。測定は、

import time
imgs = np.random.rand(100000, HEI, WID, 3)
start = time.perf_counter()
filtered_imgs = model.predict(imgs)
print('GPU:', time.perf_counter() - start)
start = time.perf_counter()
filtered_imgs = na([filter(img) for img in imgs])
print('CPU:', time.perf_counter() - start)

で行いました。(3, 3)、(5, 5)、(15, 15)の3種類のKERNEL_SIZEについて2つの環境で測定してみました (単位: 秒):

環境1 環境2
GPU 比較 CPU GPU 比較 CPU
(3, 3) 4.497 > 3.024 3.622 > 1.771
(5, 5) 3.318 > 3.039 3.57 > 2.555
(15, 15) 3.381 <  6.994 17.223 > 6.373

残念ながら、太字で示した「環境1の(15, 15)」以外では、CPUの方に軍配が上がりました。メインメモリとVRAMの間の転送などのオーバヘッドがあるためでしょうか。よって、GPUにフィルタリングさせるというのは速度面ではなかなかメリットが得にくいようです。特に、環境1は古いCPUに新しいGPUという組み合わせのため、効果が得られたのではないかと思います。

ここまでのまとめ

ここまでに得られた知見をまとめますと、

def make_sharp_kernel(k, shape):
N = np.prod(shape)
kernel = np.full(shape, -k / N)
centre = (na(shape) / 2).astype('i')
kernel[centre[0], centre[1]] = 1 + (N - 1) * k / N
return kernel
kernel = make_sharp_kernel(5, KERNEL_SIZE)

に対して、

model = Sequential()
model.add(Input((HEI, WID, 3)))
model.add(Conv2D(3, KERNEL_SIZE, padding='same'))
zeros = np.zeros(KERNEL_SIZE)
irs = na([[kernel, zeros , zeros ],
[zeros , kernel, zeros ],
[zeros , zeros , kernel]])
w = model.layers[0].get_weights()
w[0] = np.transpose(irs, (2, 3, 1, 0))
w[1][:] = 0
model.layers[0].set_weights(w)
filtered_imgs = model.predict(imgs)

と

def filter(img):
return cv2.filter2D(img, -1, kernel)
filtered_imgs = na([filter(img) for img in imgs])

は過渡応答を除いて同一の結果となるが、多くの場合、CPUの方が高速である、となります。

とはいえ、irsの9つの要素のうち6つは「何も出力しない」を意味するzerosなので、GPUには、本来必要な計算量の3倍の計算をさせていることは事実です。これを解消する書き方が出来れば逆転する可能性があります。使ったことは有りませんが、SeparableConv2Dというのがあるので、これを使えば、そのように記述できるかも知れません。

CNNモデルの先頭に固定のフィルタを追加する

先程のFIRフィルタの層を、最初のCNNモデルの先頭に入れてみます。

model = Sequential()
model.add(Input((HEI, WID, 3)))
model.add(Conv2D(3, KERNEL_SIZE, padding='same')) # FIR filter
model.add(…)
model.add(…)
model.add(Dense(N_CLASSES, activation='softmax'))
model.comple(…)

このConv2Dの層のフィルタ係数を上書きして、model.layers[0].trainable = Falseで「学習をOFF」にすれば、先程の

X_train = na([filter(img) for img in X_train])
model.fit(X_train / 255., y_train)
X_test = na([filter(img) for img in X_test ])
y_test_pred = np.argmax(model.predict(X_test / 255.), axis=1)

が

model.fit(X_train / 255., y_train)
y_test_pred = np.argmax(model.predict(X_test / 255.), axis=1)

だけで済むはずです。

前処理付きモデルの実験

実際に実験してみたところ、CPUでアンシャープマスクしてもGPUでアンシャープマスクしても、同等の正答率となりました。過渡応答の部分が異なりますがCIFAR-10では問題にならないようです (多くのデータセットで同じような結果になりそうですが)。

環境1 環境2
GPU 比較 CPU GPU 比較 CPU
学習 91.6 > 87.6 91.3 > 84.9
推論 3.22 <  3.754 4.4 > 4.27

学習時間については、GPUの場合は、エポック・イテレーション毎にフィルタ処理されることになり不利です。そのため、両方の環境で学習時間が伸びています。一方、推論時間については、またもや、逆転する結果となりました。古いCPUと新しいGPUの組み合わせである環境1ではGPUが有利なようです。

「エポック・イテレーション毎にフィルタ処理」のデメリットについては、大量の画像を学習させる際に「エポック・イテレーション毎に画像を読み込んで前処理」するようなことも有りますので、そのような用途では学習時間も不利にはならないかも知れません。

モデルからフィルタ係数を取り出して閲覧する

Conv層のフィルタ係数を上書きするには、(2, 3, 1, 0)でtransposeしました:

irs = na([[dilate, zeros , zeros],
[zeros , hordil, zeros],
[zeros , zeros , delta]])
w[0] = np.transpose(irs, (2, 3, 1, 0))

その逆変換はnp.transpose(w[0], (3, 2, 0, 1))ですが、上のirsと同じ形で表示するには少し工夫が必要です。具体的には以下のようにします:

import pandas as pd
w0T = np.transpose(w[0], (3, 0, 2, 1))
df = pd.DataFrame(w0T.reshape(np.prod(w0T.shape[: 2]), -1))
df.insert(10, 'B', '|')
df.insert( 5, 'A', '|')
df = df.T
df.insert(10, 'B', '-')
df.insert( 5, 'A', '-')
df = df.T
df

このようにすると、irsと同じ並びで確認することが出来ます:

  0 1 2 3 4 A 5 6 7 8 9 B 10 11 12 13 14
0 1 1 1 1 1 | 0 0 0 0 0 | 0 0 0 0 0
1 1 1 1 1 1 | 0 0 0 0 0 | 0 0 0 0 0
2 1 1 1 1 1 | 0 0 0 0 0 | 0 0 0 0 0
3 1 1 1 1 1 | 0 0 0 0 0 | 0 0 0 0 0
4 1 1 1 1 1 | 0 0 0 0 0 | 0 0 0 0 0
A – – – – – – – – – – – – – – – – –
5 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0
6 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0
7 0 0 0 0 0 | 1 1 1 1 1 | 0 0 0 0 0
8 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0
9 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0
B – – – – – – – – – – – – – – – – –
10 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0
11 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0
12 0 0 0 0 0 | 0 0 0 0 0 | 0 0 1 0 0
13 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0
14 0 0 0 0 0 | 0 0 0 0 0 | 0 0 0 0 0

それでは、実際の学習で生成されたフィルタを見てみましょう。

w1 = model.layers[1].get_weights()
w1T = np.transpose(w1[0], (3, 0, 2, 1))
w1T.shape
n = np.prod(w1T.shape[: 2])
df = pd.DataFrame(w1T.reshape(n, -1))
df = df.T
for i in range(3, n, 3)[:: -1]:
df.insert(i, -i, '--[%d]--' % (i / 3))
df = df.T
df.insert(6, 'B', '|')
df.insert(3, 'A', '|')
pd.set_option('display.max_rows', len(df))
df

32個のフィルタが表示されます:

  0 1 2 A 3 4 5 B 6 7 8
0 -0.070719 0.163171 -0.012778 | -0.004516 0.14339 -0.198109 | -0.157525 0.187025 -0.059381
1 -0.106428 0.161627 -0.008302 | -0.029651 0.208122 -0.276365 | -0.210118 0.309171 -0.112755
2 -0.166684 0.239374 -0.188182 | 0.000864 0.206156 -0.209469 | -0.164763 0.268961 -0.067114
-3 –[1]– –[1]– –[1]– | –[1]– –[1]– –[1]– | –[1]– –[1]– –[1]–
3 -0.075255 -0.004177 0.074683 | 0.061647 -0.227523 0.169096 | -0.079749 -0.210931 0.176043
4 0.203777 -0.123092 -0.054826 | 0.074238 -0.329145 -0.129612 | 0.30644 -0.242658 -0.058283
5 0.133595 0.195355 -0.175719 | 0.056706 0.142824 -0.217981 | 0.123844 0.156035 -0.066515
-6 –[2]– –[2]– –[2]– | –[2]– –[2]– –[2]– | –[2]– –[2]– –[2]–
6 -0.078621 0.093766 0.022708 | -0.047331 0.051828 0.025519 | -0.232535 -0.012331 0.137472
7 -0.137275 -0.159565 0.182613 | -0.039967 -0.028399 0.068846 | -0.125821 -0.071645 0.225505
8 0.127636 0.125152 -0.197608 | 0.21695 -0.039961 -0.268298 | 0.282917 -0.02403 -0.201318
-9 –[3]– –[3]– –[3]– | –[3]– –[3]– –[3]– | –[3]– –[3]– –[3]–
9 0.083142 -0.058618 0.042956 | 0.158082 0.036495 -0.242956 | -0.096894 -0.040641 -0.211612
10 -0.024678 0.172336 -0.111006 | 0.028266 0.173756 -0.037954 | 0.128748 0.024213 -0.143419
11 -0.140335 0.043694 -0.039942 | 0.112872 0.075898 -0.14014 | -0.078681 0.216014 -0.095654

見た感じ水平方向のハイパスフィルタ的なものが多いようです。1つ目のフィルタ (行番号0～2) を試してみましょう。

irs = np.transpose(w1[0], (3, 2, 0, 1))[0]
img_filterd = np.transpose([cv2.filter2D(X_train[0][:, :, p], -1, irs[p]) for p in range(3)], (1,2,0))
img_filterd -= np.min(img_filterd)
plt.imshow(img_filterd / np.max(img_filterd))

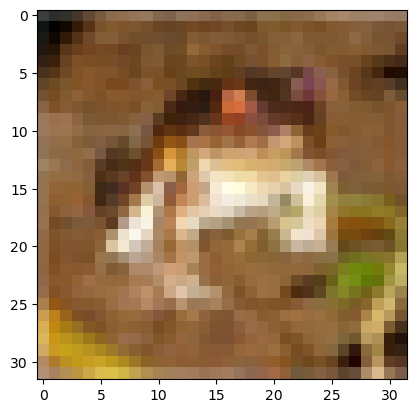
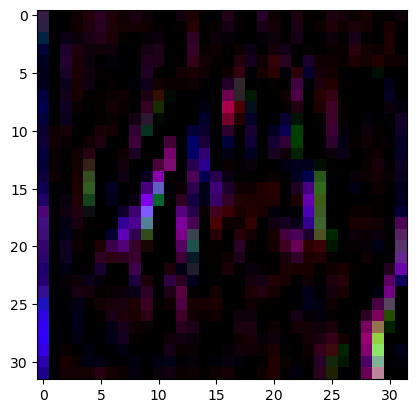
何だか怖い感じの画像になってしまいましたが、水平方向のハイパスフィルタなので、物体の垂直方向の境界線が抽出されています。今回のCNNでは、このようなフィルタ処理が、CIFAR-10の画像を認識するのに適しているということで構築された (そして、この学習済みモデルで推論を実行するたびに、内部ではこのような画像が生成されている) ということが「おわかりいただけただろうか」と思います。

まとめ

KerasのConv2Dについて、フィルタ係数がどのように格納されているのか調べ、上書きすることでFIRフィルタ処理が行えることを確認しました。また、学習結果のフィルタ係数を取り出し、サンプル画像に適用する方法についても確認できました。

今後は、どんな画像データセットに対して、どんなフィルタが構築されるのか、調査してみたいと思います。