技研のまつけんです。

 

前回の記事で予告しました通り、今回はPowerPointやExcelの“グラフ”から数式を作ってみたいと思います。前回のプログラムを少し書き換えて、

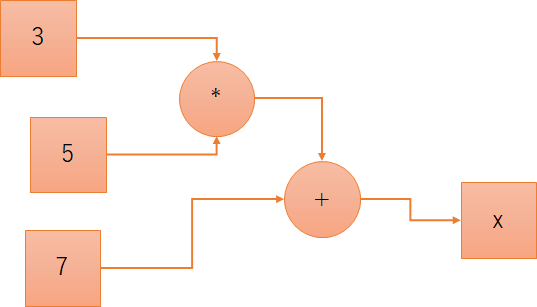
というグラフを数式に変換し、計算もさせてみたいと思います:

x = ( ( 3 * 5 ) + 7 ) --> 22

ライブラリなどのインポート

前回と同様です:

from bs4 import BeautifulSoup
import numpy as np ; na = np.array
import pandas as pd

XML読み込み

まずは、前回と同様にslideをXMLとして読み込みます:
SLIDE_NO = 1
with open('arrow_diagramme/ppt/slides/slide%d.xml' % SLIDE_NO) as f:
s = f.read()
soup = BeautifulSoup(s, 'html.parser') # または soup = BeautifulSoup(s, 'xml')

図形と矢印の抽出

前回とは異なり、今回は、すべてのオブジェクトをまとめて辞書にします:

objs = {}
for p in soup.find_all('p:sp'):
idno = int(p.find('p:cnvpr').get('id'))
prst = p.find('a:prstgeom').get('prst')
texts = [t.string for t in p.find_all('a:t')]
text = ''.join([t if '\n' != t[-1] else t[: -1] for t in texts])
objs[idno] = (text, prst)
objs = {idno: (i, *objs[idno]) for i, idno in enumerate(objs)}
print(objs)
# {4: (0, '3', 'rect'), 5: (1, '5', 'rect'), 9: (2, '*', 'ellipse'), 19: (3, '7', 'rect'), 22: (4, '+', 'ellipse'), 29: (5, 'x', 'rect')}

{図形のID番号: (通し番号, 文字列, 図形種別)}という形式です。通し番号は、読み込み結果を隣接行列として表示させて動作を確認するために付加しているので、最終的には無くしても問題ありません。

矢印のリスト生成は前回と一緒です:

edges = []
for p in soup.find_all('p:cxnsp'):
start = int(p.find('a:stcxn' ).get('id'))
end = int(p.find('a:endcxn').get('id'))
if p.find('a:headend') is not None:
edges.append((end, start))
if p.find('a:tailend') is not None:
edges.append((start, end))
print(edges)
# [(4, 9), (5, 9), (9, 22), (19, 22), (22, 29)]

隣接行列の確認

では、objsとedgesから隣接行列を作って、動作確認をしてみましょう:

mat = np.zeros([len(objs)] * 2, dtype='str').tolist()
for i in range(len(objs)):
mat[i][i] = '*'
for start, end in edges:
if start in objs and end in objs:
mat[objs[start][0]][objs[end][0]] = '1'
index = [(idno, objs[idno][1]) for idno in objs]
df = pd.DataFrame(mat, index=index, columns=index)
df.to_csv('slide%d.csv' % SLIDE_NO)

CSVとして保存された隣接行列です (自分自身への矢印は存在しないという仮定から、対角成分は’*’で埋めています):

(4, ‘3’) (5, ‘5’) (9, ‘*’) (19, ‘7’) (22, ‘+’) (29, ‘x’)
(4, ‘3’) * 1
(5, ‘5’) * 1
(9, ‘*’) * 1
(19, ‘7’) * 1
(22, ‘+’) * 1
(29, ‘x’) *

まずは、垂直方向に眺めてみます。左から3列目は3と5が*に入力されていることを示し、5列目は*と7が+に入力されていることを示します。また、最も右の列を見ると、+がxに入力されていることがわかります。

次に、水平方向に眺めてみます。最終行だけが全て空欄であることから、xだけはそこから出ていく矢印が無く、それ以外はそこから出ていく矢印が存在するということがわかります。つまり、数式はx=で始まるものが1つだけ生成されるべき、ということです。

最終出力となる図形の取り出し

そのような最終出力にあたる図形を抜き出します。以下のようにsetとして引き算をすれば

edges_T = na(edges).T
finals = set(edges_T[1]) - set(edges_T[0])
for final in finals:
print(final, objs[final])
# 29 (5, 'x', 'rect')

のように、最終出力の図形のIDが得られます。ただし、出力の図形が複数ある場合に順番が保存されないので、リスト内包表記で処理します:

edges_T = na(edges).T
finals = [e for e in edges_T[1] if e not in edges_T[0]]
for final in finals:
print(final, objs[final])
# 29 (5, 'x', 'rect')

数式への変換と演算の実行

では、いよいよ、数式へと変換し、数式と計算結果を表示させてみます:

def get_froms(edges, idno):
return [e[0] for e in edges if e[1] == idno]
VERBOSE = False
stats = [] # statements
for final in finals:
stat = [objs[final][1], '=', get_froms(edges, final)[0]]
flag = True
while flag:
print(' '.join(['<<%d>>' % (s) if isinstance(s, int) else s for s in stat]), '\t', stat) if VERBOSE else None
flag = False
for i, s in enumerate(stat):
if isinstance(s, int):
flag = True
if 'rect' == objs[s][2]:
s1 = [objs[s][1]]
else:
op = objs[s][1]
s1 = ['(']
for f in get_froms(edges, s):
obj = objs[f]
if 'rect' == obj[2]:
s1 += [objs[f][1], op]
else:
s1 += [f, op]
s1 = s1[: -1] + [')']
break
if flag:
stat = stat[: i] + s1 + stat[i + 1 :]
stats.append(stat)
print('================') if VERBOSE else None
for stat in stats:
stat_str = ' '.join([str(s) for s in stat])
exec(stat_str)
print(stat_str, '-->', eval(''.join(stat[2 :])))
# x = ( ( 3 * 5 ) + 7 ) --> 22

get_froms()は指定したIDを持つ図形に、どのIDの図形から矢印が入力されているかを返す関数です。数式 (プログラミング言語でいう「代入文」なのでstatement) は最終的にstatsに格納されます。二分木のような構造 (3本以上の入力も許容しているので正確には二分木ではない) を処理するにあたって、再起呼び出しを使わずに処理しています。VERBOSE=Trueにすると、変換の途中過程が表示されます:

x = <<22>> ['x', '=', 22]
x = ( <<9>> + 7 ) ['x', '=', '(', 9, '+', '7', ')']
x = ( ( 3 * 5 ) + 7 ) ['x', '=', '(', '(', '3', '*', '5', ')', '+', '7', ')']
================
x = ( ( 3 * 5 ) + 7 ) --> 22

statはstrとintからなるリスト形式で、図形のID番号がintで、図形の中に書かれた文字列がstrで格納されます。二分木的な構造が展開されるとintの要素が無くなります。よって、intの要素が一つも無くなると、flagがFalseのままとなり、ループから抜けます。
1行目は「xにはID=22が代入されている」ことを示しています。2行目では、「ID=22」が展開されて「ID=9と7の和」になっています。3行目で「ID=9」が「3と5の積」に展開されています。ここで、処理が終了となります。
演算の実行は、xと=を除いたものを''.join()してevalするだけです。

複雑なグラフの変換と演算

では、こちらの複雑なグラフに対しても実行してみましょう。

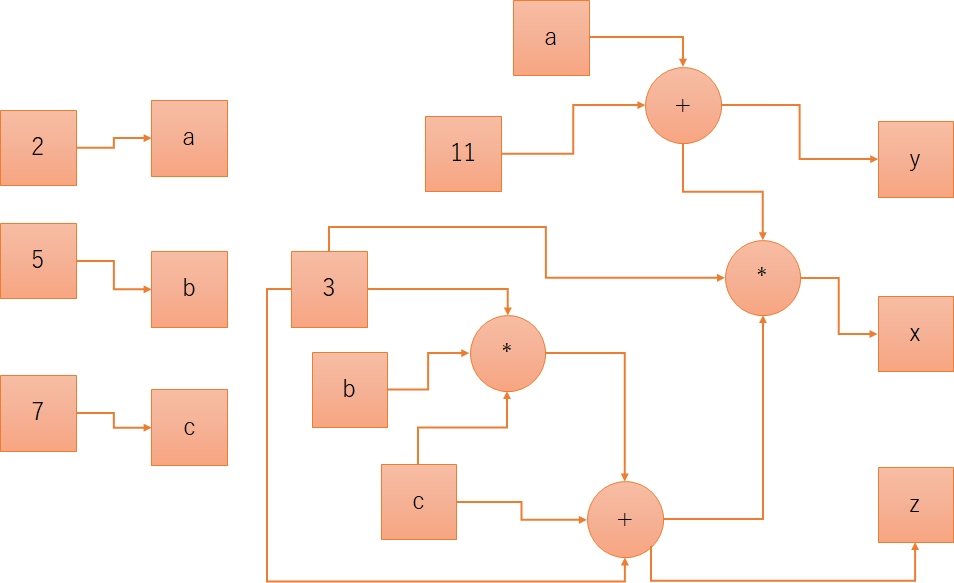
VERBOSE=Trueで実行した結果は、以下の通りです:

a = <<10>> ['a', '=', 10]
a = 2 ['a', '=', '2']
================
b = <<31>> ['b', '=', 31]
b = 5 ['b', '=', '5']
================
c = <<51>> ['c', '=', 51]
c = 7 ['c', '=', '7']
================
x = <<46>> ['x', '=', 46]
x = ( <<22>> * 3 * <<26>> ) ['x', '=', '(', 22, '*', '3', '*', 26, ')']
x = ( ( <<9>> + c + 3 ) * 3 * <<26>> ) ['x', '=', '(', '(', 9, '+', 'c', '+', '3', ')', '*', '3', '*', 26, ')']
x = ( ( ( 3 * b * c ) + c + 3 ) * 3 * <<26>> ) ['x', '=', '(', '(', '(', '3', '*', 'b', '*', 'c', ')', '+', 'c', '+', '3', ')', '*', '3', '*', 26, ')']
x = ( ( ( 3 * b * c ) + c + 3 ) * 3 * ( a + 11 ) ) ['x', '=', '(', '(', '(', '3', '*', 'b', '*', 'c', ')', '+', 'c', '+', '3', ')', '*', '3', '*', '(', 'a', '+', '11', ')', ')']
================
y = <<26>> ['y', '=', 26]
y = ( a + 11 ) ['y', '=', '(', 'a', '+', '11', ')']
================
z = <<22>> ['z', '=', 22]
z = ( <<9>> + c + 3 ) ['z', '=', '(', 9, '+', 'c', '+', '3', ')']
z = ( ( 3 * b * c ) + c + 3 ) ['z', '=', '(', '(', '3', '*', 'b', '*', 'c', ')', '+', 'c', '+', '3', ')']
================
a = 2 --> 2
b = 5 --> 5
c = 7 --> 7
x = ( ( ( 3 * b * c ) + c + 3 ) * 3 * ( a + 11 ) ) --> 4485
y = ( a + 11 ) --> 13
z = ( ( 3 * b * c ) + c + 3 ) --> 115

statsに登録される順番は、最終出力の矩形がXMLに登場する順番です。aやbへの代入より前に、xやyに関する演算は出来ないので、PowerPoint上で、a、b、cの矩形がx、y、zの矩形よりも「背面」になるように設定します。

また、引き算や割り算のように順番を指定したい場合は、各矢印のidxを使うと良さそうです。idxを見れば、矢印が上下左右のどこに接続されているのか知ることが出来ます。試しに、このようなグラフ:

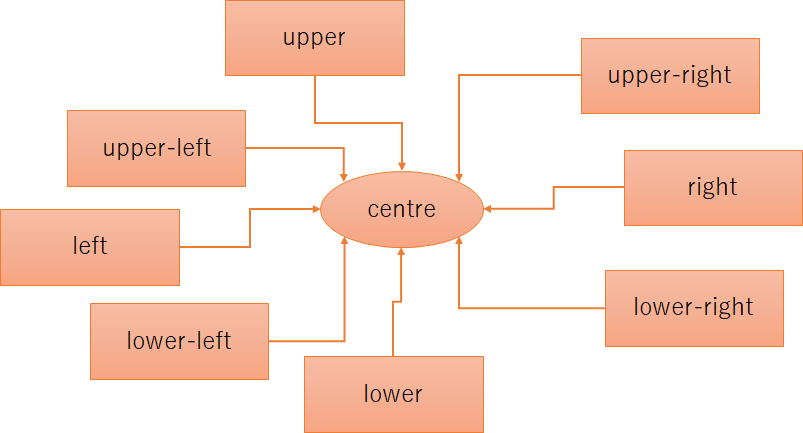
を作り、隣接行列にidxを入れてみます:

edges = []
for p in soup.find_all('p:cxnsp'):
start = int(p.find('a:stcxn' ).get('id'))
start_idx = int(p.find('a:stcxn' ).get('idx'))
end = int(p.find('a:endcxn').get('id'))
end_idx = int(p.find('a:endcxn').get('idx'))
if p.find('a:headend') is not None:
edges.append((end, start, start_idx))
if p.find('a:tailend') is not None:
edges.append((start, end, end_idx))
mat = np.zeros([len(objs)] * 2, dtype='str').tolist()
for i in range(len(objs)):
mat[i][i] = '*'
for start, end, idx in edges:
if start in objs and end in objs:
mat[objs[start][0]][objs[end][0]] = idx

生成された隣接行列のCSV (抜粋) です:

(17, ‘centre’)
(17, ‘centre’) *
(3, ‘upper’) 0
(43, ‘upper-left’) 1
(21, ‘left’) 2
(64, ‘lower-left’) 3
(8, ‘lower’) 4
(71, ‘lower-right’) 5
(37, ‘right’) 6
(76, ‘upper-right’) 7

「上」から反時計回りに0～7が割り振られていることが分かりました。この情報を使えば、引き算や割り算の順序も表現できそうです。

まとめ

今回は、PowerPointやExcelの“グラフ”を数式に変換するものを作ってみました。次回は、これまでの実験の結果を踏まえて、機械学習のモデル (特に、ResNetやU-Netのような枝分かれのあるもの) をPowerPointでグラフとして描き、それをKerasやPyTorchのソースコードに変換するものを作ってみたいと思います。どうぞ、お楽しみに。