運搬経路問題(VRP) は複数の運搬車が倉庫から顧客にいる場所を訪れ、顧客に荷物を渡したときに配達コスト最小化を行う数理問題です。具体的事例として下の図のように荷物の配達をするトラック総運行距離を最小化するように計画を作成すると考えたら良いかも知れません。
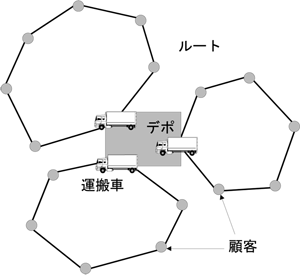
倉庫から顧客への運搬に着目する場合は「配送計画問題」と呼ばれることも多いです。ここでVRP (vehicule routing problem)問題と呼ぶこととします。
運搬経路問題は様々な種類があります。よく用いられているモデルを紹介します。
- CVRP (Capacitated Vehicle Routing Problem) : 車両ごとに最大容量制約が設けられています。
- VRPTW (Vehicle Routing Problem with Time Windows):顧客ごとの配達希望時間帯制約が設けられています。
- DCVRP (Distance Constrained VRP):車両が走行できる距離の制約が設けられています。
- HVRP (Heterogeneous fleet VRP):車両の種類が複数ある場合のVRPです。
- MDVRP (Multi Depots VRP):車庫は複数ある場合のVRPです。
- VRPB (VRP with Backhaul): 車両は全ての配達が終わった後に,集荷を行う場合のVRPです。
- VRPDP (VRP with Pick-up and Delivery): 集荷および配達を行う場合のVRPです。荷物の集荷が配達より先という制約が設けられています。
- PDP (Pick-up and Delivery Problem): VRPPDと似た問題設定です。
- DARP (Dial a Ride Problem): 運ぶのが人の場合のPDPで、オンデマンド型交通の配送最適化問題です。人の移動時間についての制約や目的関数が追加されます。
ここではPythonのpulpでCVRP問題を実装してみました。
運搬経路問題を解くためにグラフ理論はよく使用されます (グラフのノードとエッジに数値データが追加されます)。グラフ理論ではエッジを通るか通らないかことによって経路を選択すると考えることができるからです。
エッジに「1」を割り当てると、経路が選択されていることを意味します。ここではグラフ理論を用いるCVRP問題を説明します。
決定変数は車両(k)が経路(e_{ij})を通るかどうか評価する。
- 各顧客の場所に訪れるのは1台の車両で1度
- 車庫から出発して,車庫に戻ってくる
- 車両の最大容量を超えてはいけない
上記を踏まえて,CVRPを次のように定式化します。
図 2 のパラメータの定義に基づいて、決定変数と CVRP の目的関数の制約を定式化しました。
(1)式では目的関数である全車両の合計移動コストを最小化します。
(2)式では1台のみの車両で1度のみ各顧客を訪問するという制約を追加します。
(3)式では車庫から出発するという制約を追加します。
(4)式では各顧客の場所に来る車両数と出る車両数が同じであるという制約を追加します。
(5)式では各車両において最大容量を超えてはいけないという制約を追加します
(6)式では車庫から繋がれていない経路を除去するという制約を追加します。
(7)式では決定変数の制約を追加します。
上記の数式に基づいてpulpを用いて運搬経路問題を解くことができます。
①必要なライブラリーをインポートします。
| import numpy as np |
| import pandas as pd |
| import pulp |
| import itertools |
| from geopy.distance import great_circle |
②インプットパラメータを設定する。
| customer_count = 11 #顧客数(id=0はdepot) |
| vehicle_count = 8 #車両数 |
| vehicle_capacity = 50 #車両容量 |
| np.random.seed(seed=32) |
③車庫は新橋駅とし、正規分布を用いて顧客位置(経度、緯度)を設定します。
| # 車庫緯度・経度設定 (新橋駅位置) |
| depot_latitude = 35.682000 |
| depot_longitude = 139.775200 |
| #顧客緯度・経度設定 |
| df = pd.DataFrame({"latitude":np.random.normal(depot_latitude, 0.055, customer_count), |
| "longitude":np.random.normal(depot_longitude, 0.055, customer_count), |
| "demand":np.random.randint(15, 20, customer_count)}) |
| df.loc[0,'latitude'] = depot_latitude |
| df.loc[0,'longitude'] = depot_longitude |
| df.loc[0,'demand']= 0 |
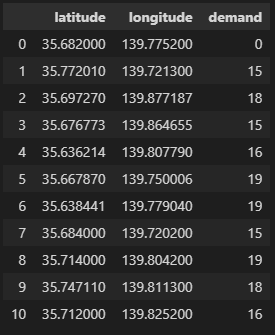
各顧客の位置と荷物量次のようになります。
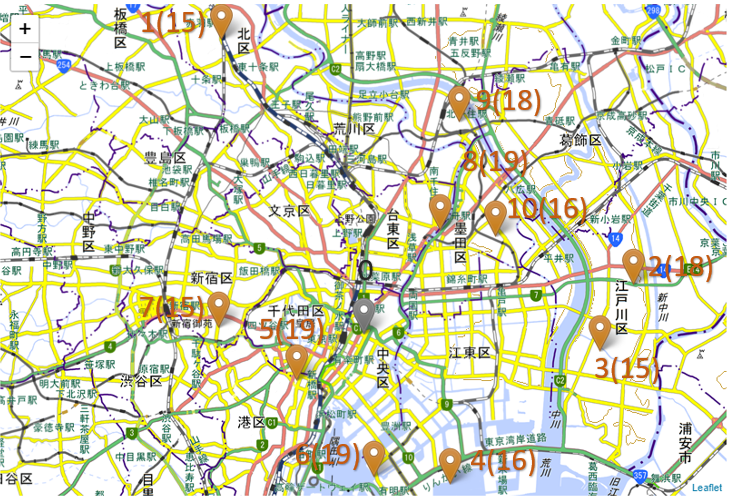
leafletを用いてマップも作成します。
④コストは移動距離とし、大円理論で各ノード距離を評価します。
| dist = [[great_circle((df.loc[i,'latitude'],df.loc[i,'longitude']), |
| (df.loc[j,'latitude'],df.loc[j,'longitude'])).meters |
| if i != j else 0 for j in range(0,customer_count)] for i in range(0,customer_count)] |
| cost=np.array(dist) |
次ヒートマップを作成します。
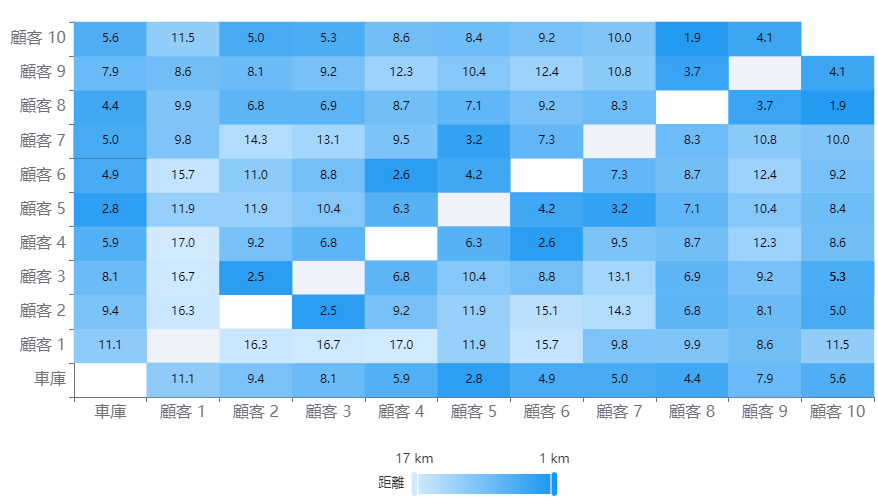
マップから最短距離は1.9km(8⇔10)であり最長距離は17.0km(1⇔4)であることが分かります。
⑤上記の定式化を,最適化問題を簡単にモデリングできるライブラリ「PuLP」を用いて実装します。
必要な車両数は少ないほうが良いので,最適解が出たら終了するようにします。
| for vehicle_count in range(1,vehicle_count+1): |
| # 問題の宣言 |
| problem = pulp.LpProblem("CVRP", pulp.LpMinimize) |
| # 決定変数 |
| x = [[[pulp.LpVariable("x%s_%s,%s"%(i,j,k), cat="Binary") if i != j else None for k in range(vehicle_count)]for j |
| in range(customer_count)] for i in range(customer_count)] |
| # 目的関数 |
| problem += pulp.lpSum(cost[i][j] * x[i][j][k] if i != j else 0 |
| for k in range(vehicle_count) for j in range(customer_count) for i in range (customer_count)) |
| # 制約 |
| # (2)式,各顧客の場所に訪れるのは1台の車両で1度である |
| for j in range(1, customer_count): |
| problem += pulp.lpSum(x[i][j][k] if i != j else 0 for i in range(customer_count) for k in range(vehicle_count)) == 1 |
| #(3)式, depotから出発して,depotに戻ってくる |
| for k in range(vehicle_count): |
| # デポを出発した運搬車が必ず 1つの顧客から訪問を開始することを保証する制約条件 |
| problem += pulp.lpSum(x[0][j][k] for j in range(1,customer_count)) == 1 |
| # 必ず 1 つの顧客から運搬車がデポへ到着すること保証する制約条件 |
| problem += pulp.lpSum(x[i][0][k] for i in range(1,customer_count)) == 1 |
| #(4)式, ある顧客の所に来る車両数と出る車両数が同じ |
| for k in range(vehicle_count): |
| for j in range(customer_count): |
| problem += pulp.lpSum(x[i][j][k] if i != j else 0 for i in range(customer_count)) - pulp.lpSum(x[j][i][k] for i in range(customer_count)) == 0 |
| #(5)式, 各車両において最大容量を超えない |
| for k in range(vehicle_count): |
| problem += pulp.lpSum(df.demand[j] * x[i][j][k] if i != j else 0 for i in range(customer_count) for j in range (1,customer_count)) <= vehicle_capacity |
| #(6)式, 部分巡回路除去制約 |
| subtours = [] |
| for i in range(2,customer_count): |
| subtours += itertools.combinations(range(1,customer_count), i) |
| for s in subtours: |
| problem += pulp.lpSum(x[i][j][k] if i !=j else 0 for i, j in itertools.permutations(s,2) for k in range(vehicle_count)) <= len(s) - 1 |
| #最適化問題を解く |
| #最適解が出たら終了 |
| if problem.solve() == 1: |
| print('車両数:', vehicle_count) |
| print('目的関数値:', pulp.value(problem.objective)) |
| break |
次のように結果は出力された。
車両数: 4
目的関数値: 77588.808389981
全顧客をまわるのに車両が4台必要であることがわかりました。結果をマッピングしてみます。
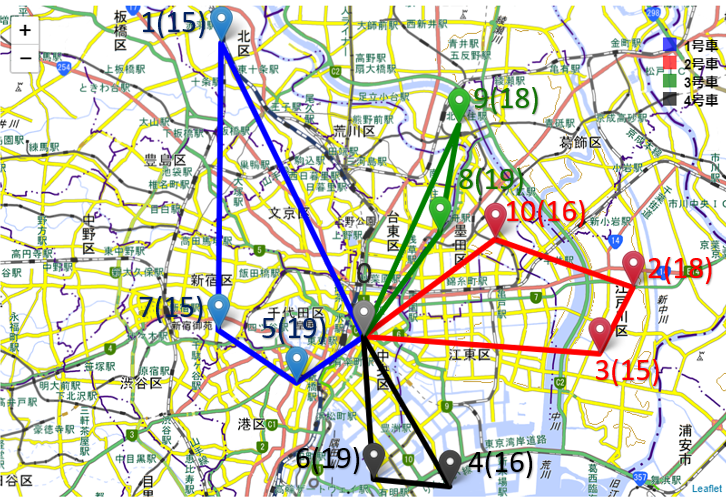
顧客数や車両最大容量等のインプットパラメータを振ってモデル可視化を行ってみます。
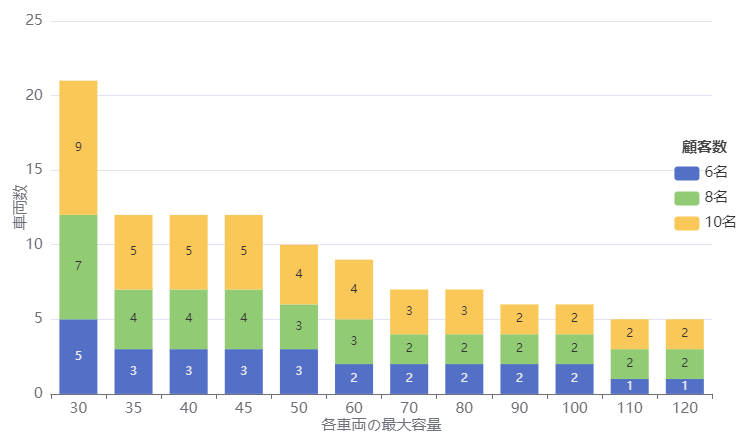
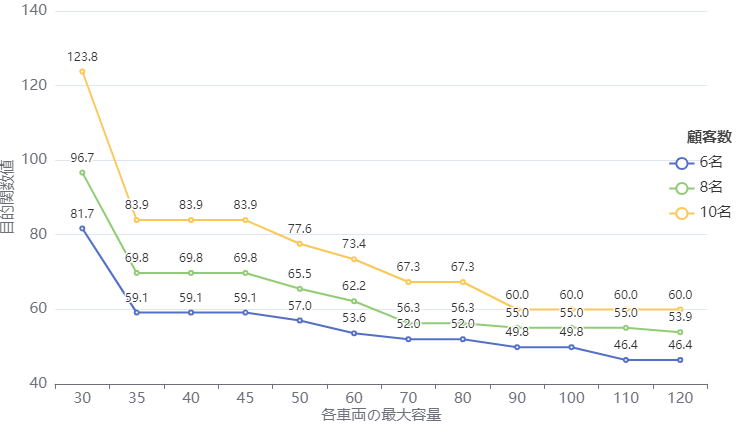
顧客数は増えれば増えるほど必要な車両数・目的関数値は高くなり、各車両の最大容量は増えれば増えるほど車両数・目的関数値は低くなります。例えば、顧客数:6人・最大容量:120の場合は市車両数=1台・目的関数値=46.4になることに対して顧客数:10人・最大容量:30の場合は市車両数=9台・目的関数値=123.8になります。顧客数も車両最大容量も大きな影響を与えることが分かります。
この記事では最大容量制約付き「運搬経路問題」の定式化と,「PuLP」を用いた実装について説明しました.しかし、紹介したモデルは単純です(例えばすべての車両の容量は同じです)。
したがって、モデルの適用領域は非常に狭いので今後より複数な制約を考慮するモデルの実装を考えてみたいと思います。




