統計学の視点から良いモデルとは何かを考える

こんにちはAITCのmasato です。

今回は「統計学の視点から良いモデルとは何か」を考えていきたいと思います。
統計学モデルや機械学習モデルで、良いモデルをいかに判断するかというのは非常に重要だと思います。

統計学モデルを勉強していると、機械学習モデルと良いモデルについての捉え方は共通していることに気付きます。
また、機械学習モデルに対して、統計学モデルは良いモデルについて数学的に理解しやすいと思っています。

そこで、あえて統計学の視点から学ぶことで、
「良いモデル」を統計学的に明確化してみましょうというのが今回のテーマです。

機械学習での、「過学習」「汎用性」などの用語の理解にもつながると思います。

それでは本題に入っていきましょう！

さて先ほどから「統計モデル」という言葉を多用していますが、
そもそも「統計モデル」とは何でしょうか？

例えば、次のようなXとYの関係のデータが得られたとき
私たちは、そこに比例関係があるなと考える人が多いでしょう。

すなわち、Xが増加するに従いYも増加する。そんな比例関係がこのデータにはあるということです。

私たちはこのような比例関係を直線の数式で表現してY=aX+bなどの直線を当てはめることができます。
このようなデータを数式で表現化されたものが統計モデルなのです。

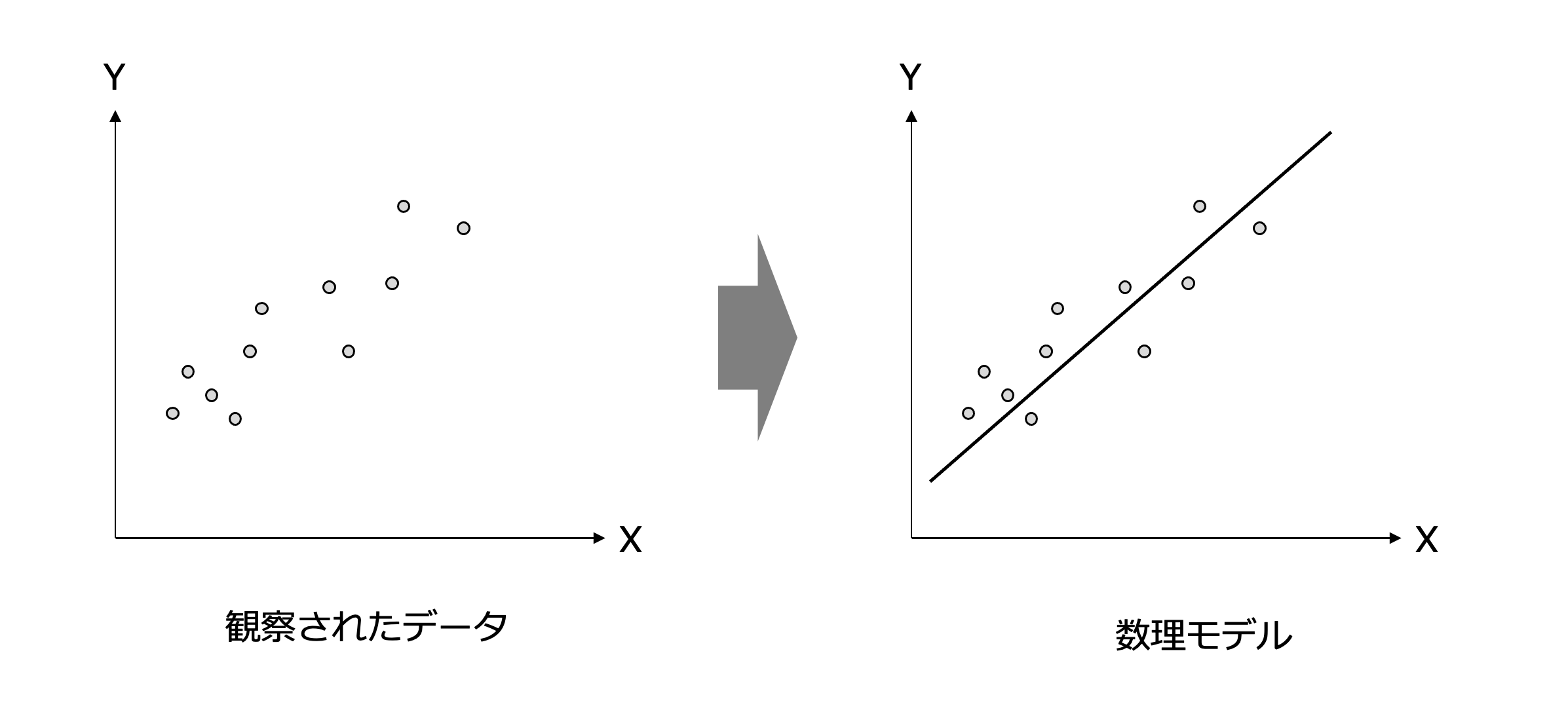
しかし、みなさんはなぜこのデータを見て比例関係があると思うのでしょうか。

それは、これまでの経験から次のように思っているからではないでしょうか？

「世の中の現象には真の法則が働いている。
その法則からノイズをともなってデータが現れる」と。

つまり、統計モデルを作るとき、私たちは真の法則があるという信念の元に
その法則を統計モデルで表現しようとしています。

そして、その統計モデルで表現された法則を用いて予測や分析していくこともできるでしょう。
これが、統計学モデリングの目標なのです。

さてこの統計モデルについて作り方を学びつつ、良いモデルについて考えていこうと思います。

次のような10個のデータが与えられた時に統計モデルを作ってみましょう。

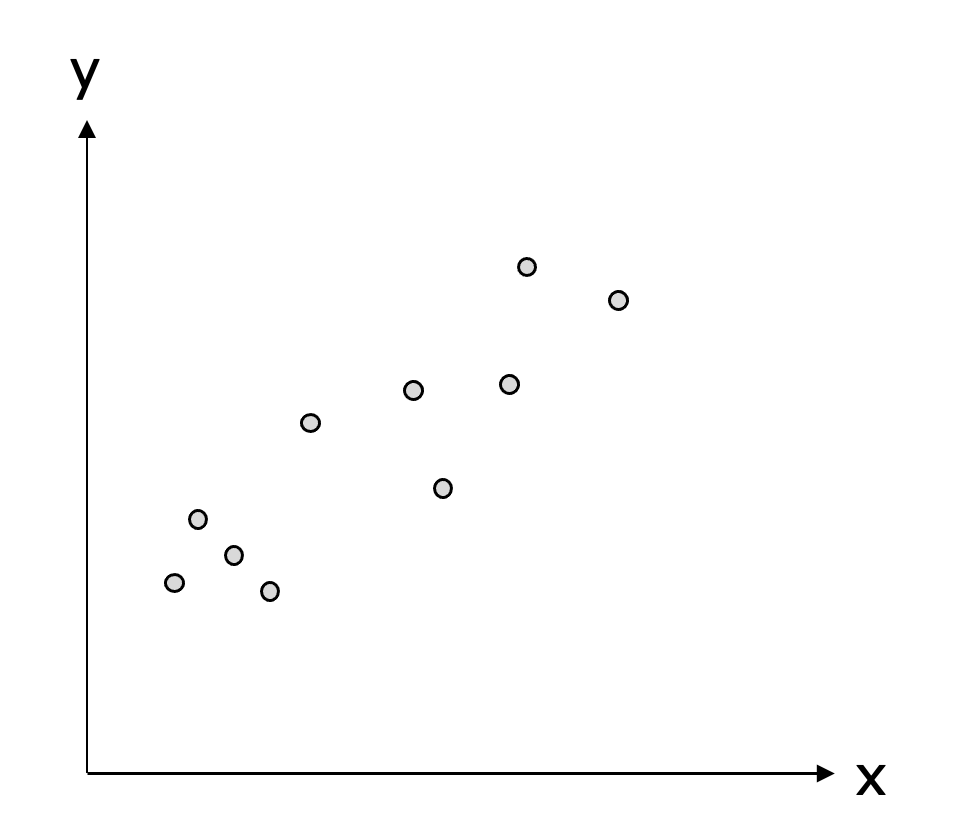
データから統計モデルを作る際、こんな式が法則として成り立たせているのではないかとモデルを仮定することから始めます。

例えば、先ほどのデータが与えられた時
「比例関係があるな」
「真の法則からバラツキをともなって、このデータは得られたのだな」
と考えることができます。
このような真の法則である直線から誤差をともなってデータが発生という考察から
各データは以下のような式で考えることができます。

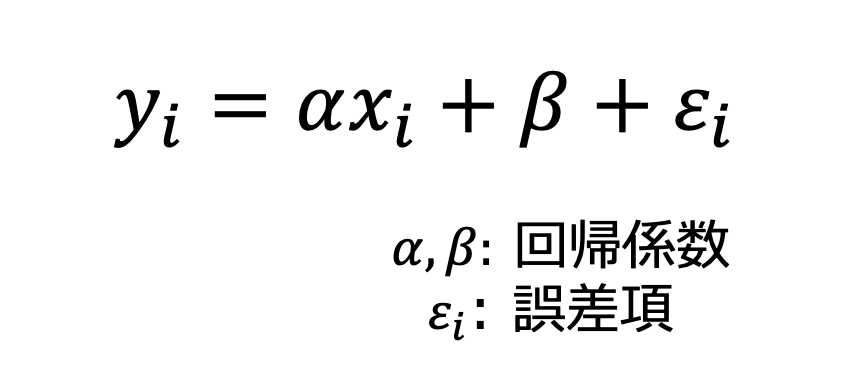
右下の添字であるiは、データを識別する番号です。具体的に「1,2,…」などの数字が入ります。x, y, εは各データの値なのだなと思えば問題ありません。

上の式では真の法則を直線の傾きと切片で表しています。
また、真の法則にあるデータのxの値を与えた時の真の値からのバラツキを誤差項で表しています。

図として表すと次のようになります。

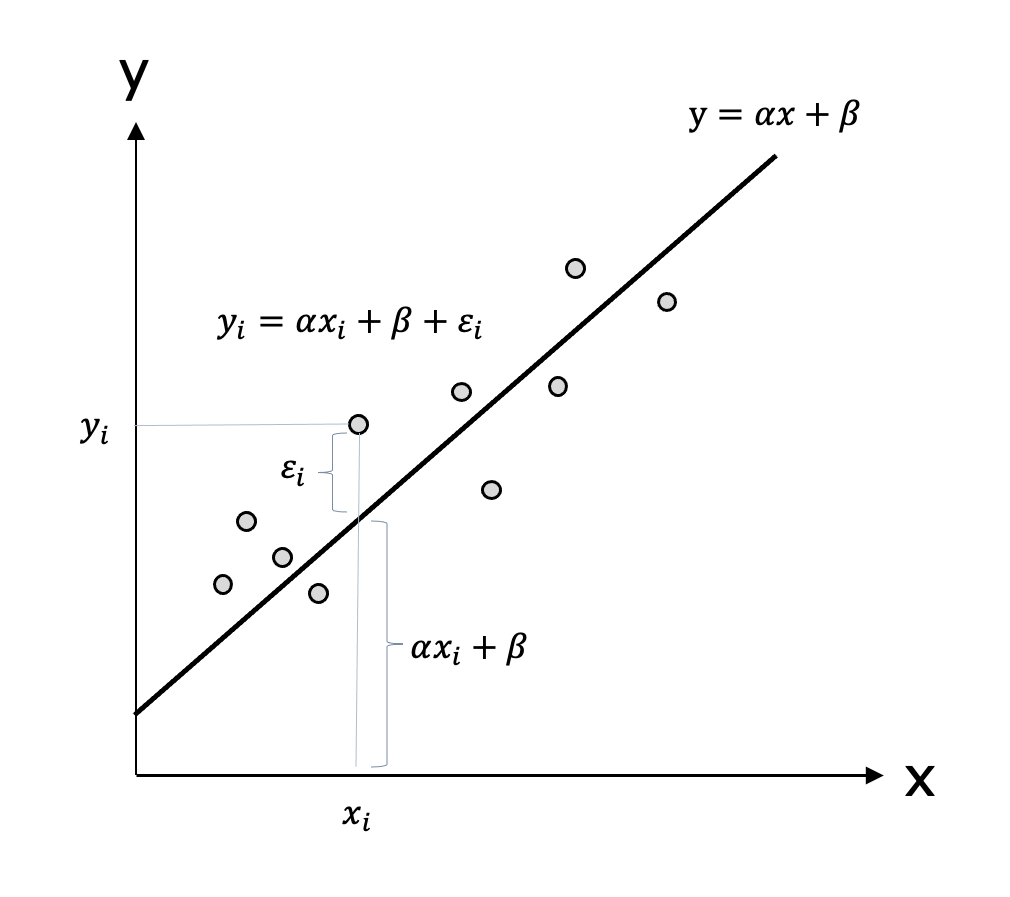
さて誤差項は定まった数ではなく、データのバラツキを考えるとランダムな値です。

そこで誤差項が何らかの分布に従っていると考えます。
代表的な確率分布として正規分布があげられます。

正規分布について簡単に説明すると
「平均値の近くで多くの観測データが生じやすく、平均値から離れれば離れるほど生じにくくなるデータを表す確率分布」です。

正規分布に従うデータを例に取ったほうがわかりやすいですね。
身長は正規分布に従うと言われていますので、日本の成人男性の身長を例とします。
日本の男性の平均身長は約170センチと言われています。
経験的にも、170センチあたりの身長の男性が多いですよね。190センチ以上はかなり稀です。
もし、私たちが道で出会う男性に身長を聞いた時、170センチあたりのデータが得られる確率が高く、平均から離れた190センチ以上のデータを得られる確率は低いでしょう。

ある身長データの得られやすさを
この身長の正規分布をグラフで表すと次のようになります。

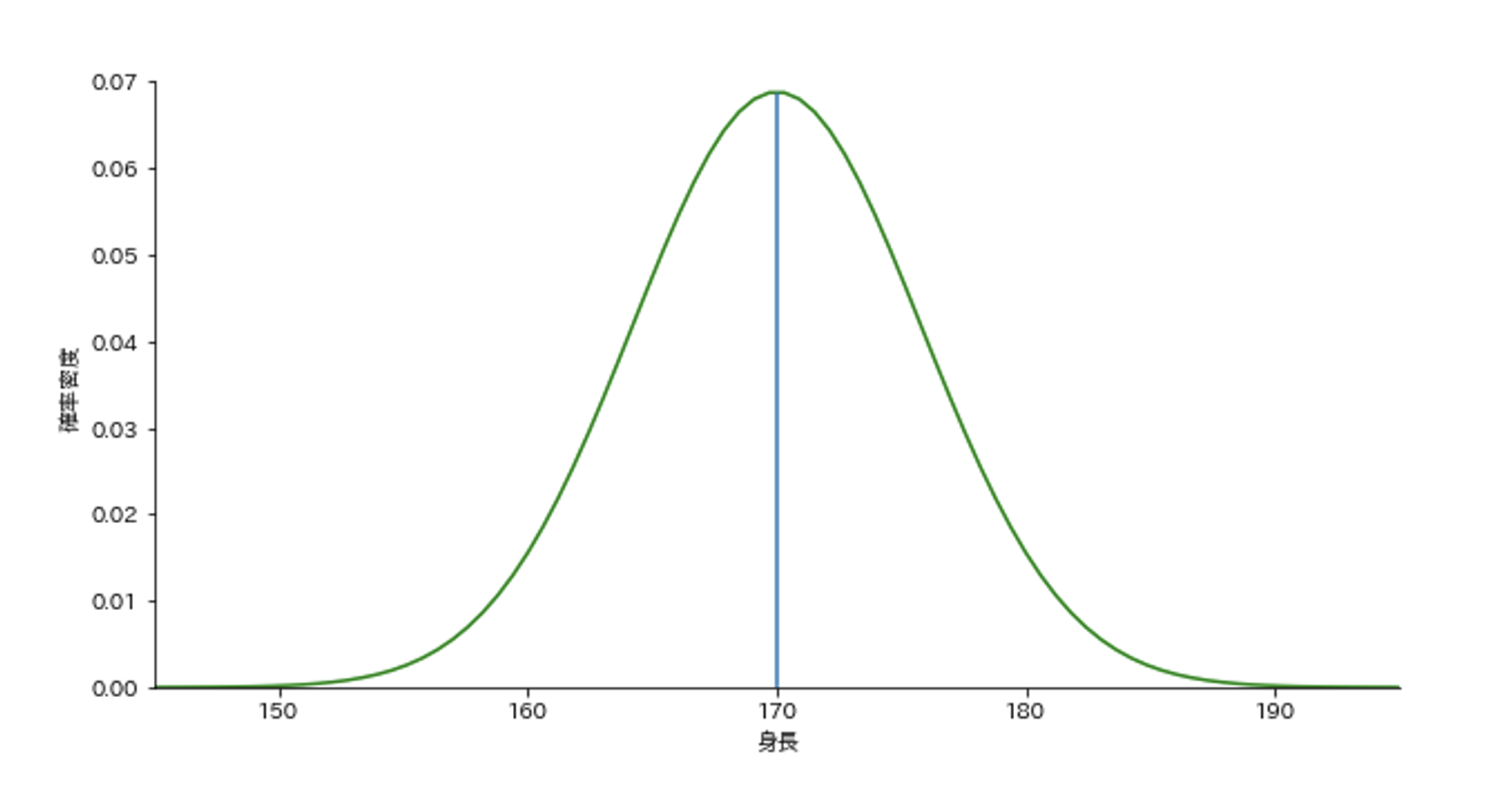
細かいところは抜きにして、この正規分布の読み取り方を説明しましょう。
正規分布は山の形状をしています。
山の高さはデータの得られやすさを表しています。このことから、平均身長170センチ付近のデータが得られやすいことや、150センチ以下や190センチ以上はデータが得られにくいことを読み取ることができます。

大まかなところがわかったところで正規分布について、次の図をもとに詳しく説明していきます。

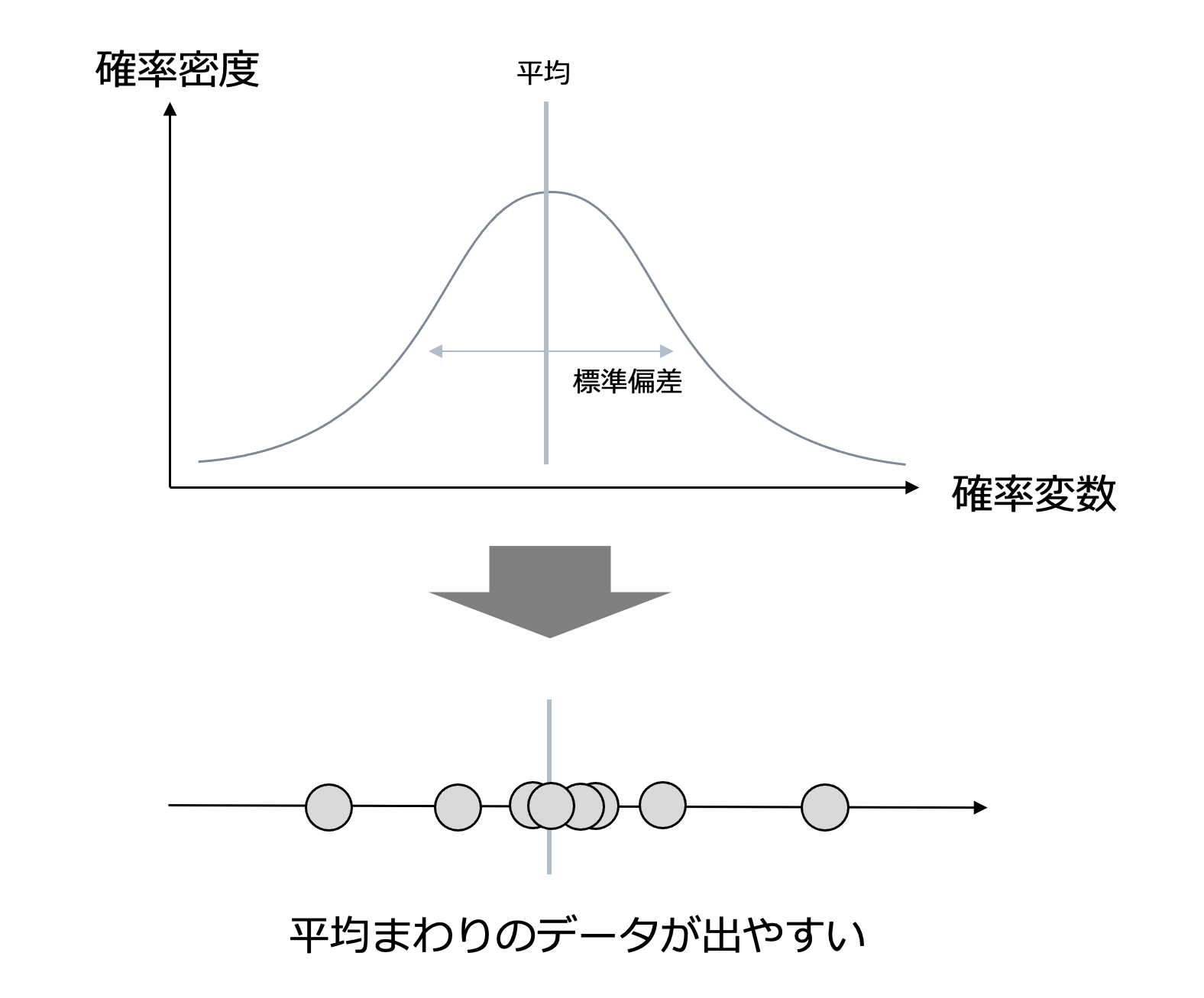
まず正規分布の特徴ですが、左右対称の山の形状をしています。

山の位置や幅を決めるのが平均や標準偏差です。

平均は正規分布の中心になります。なので平均によって山の位置が決まります。
平均が170の正規分布に従っているなら、そこから観測できるデータは170のあたりでデータが得られやすいことを意味します。

標準偏差が大きい正規分布に従うほど、平均からのバラツキが大きいデータが現れます。
山の幅はそのバラツキの度合いを表しています。

そして正規分布の横軸と縦軸についてですが

横軸の確率変数は値と確率密度が紐づいているものです。
先ほどの例だと身長が確率変数です。

縦軸が確率密度でデータが起こりうる確率の高さを表しています。
確率密度が大きいほどその事象は起こりやすいと言えます。

さて、この正規分布を誤差項とした線形回帰モデルを考えましょう。
誤差項が平均0で標準偏差σの正規分布に従う時、次の式で表すことにしましょう。

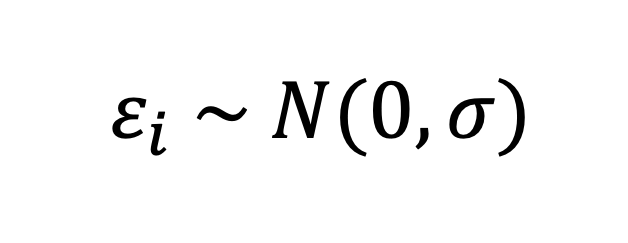
よって次の式で、線形モデルを表してみると
私たちが値を変化させることができるパラメータは次の3つになります。

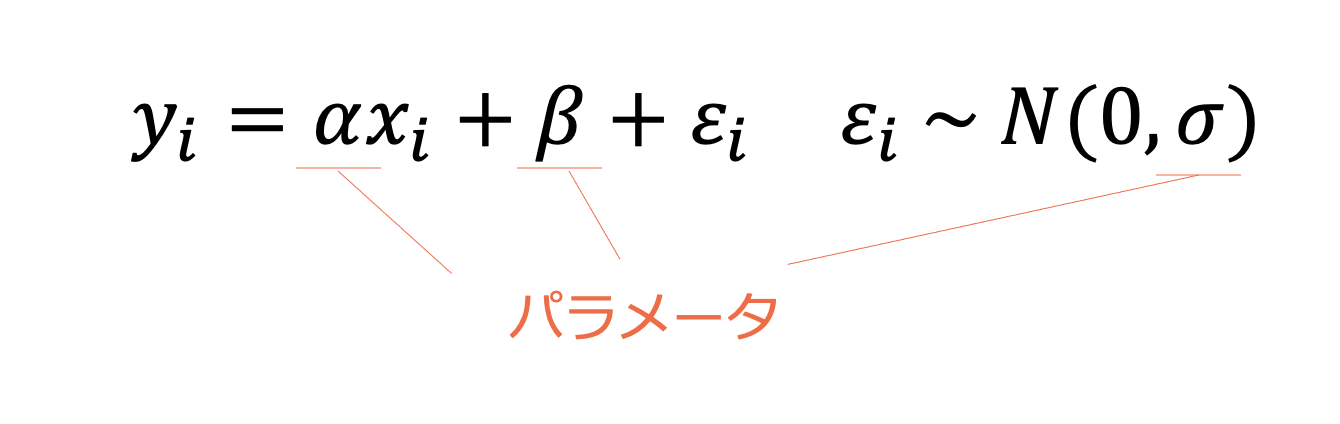
このパラメータを変化させることで、回帰直線の傾きや、分散を変化させることができます。
ここからはどのパラメータであれば、データに合ったモデルと言えるのかを考えていくことになります。

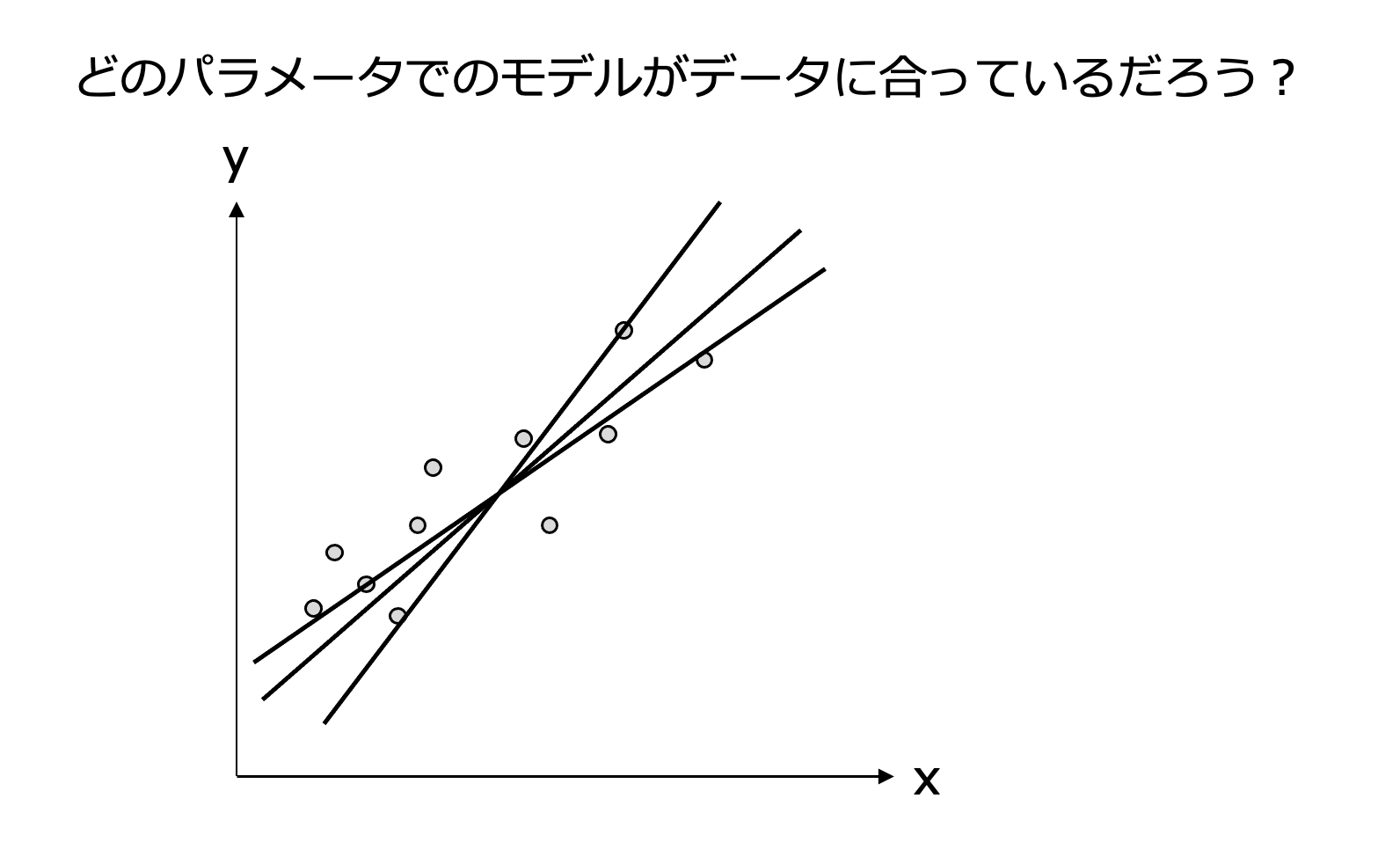
データに合うとはどうやって判断するか。
その鍵がもっともらしさという統計学的な考え方です。

統計学では
「世の中で起きていることは、起きる確率が大きいこと」という考えに従っています。
これは私たちが日常的によく使っていることです。
例えば、「ニャー」という鳴き声が聞こえてきました。どの動物の鳴き声だと思いますか。

当然猫だと思いますよね。犬などが「ワン」と鳴くのはこれまでの経験からまずあり得ないと考えます。
でも1万匹に1匹ぐらいは「ニャー」と鳴くかもしれません。
しかし私たちは、そういうレアなケースはまず起こり得ないと考えて、
一番「ニャー」と鳴くであろう動物の「猫」を鳴き声の原因と考えます。

このように、観測された現象が生じる確率がもっとも大きくなる原因をもっともらしいとして採用しているんです。これを最尤原理といいます。
統計学は、この最尤原理に従っています。

さて、先ほどの例は
「ニャー」というデータが得られたとき、どの動物の鳴き声かを考えることでしたが
今度は「観測データ」が得られたとき、どの分布に従っているかを考えてみましょう。

どのようにしてデータがある分布に従っているかを判断すればよいでしょうか？

これも最尤原理の考えに従ってみましょう。
つまり観測された現象が生じる確率がもっとも大きくなる分布をもっともらしいとして採用すれば良いのです。

さて次のように、観測データがどちらの分布にもっともらしいかを考えてみましょう。
観測データを確率変数の軸にプロットしています。赤と青の正規分布のどちらに従っているのがもっともらしいでしょうか。

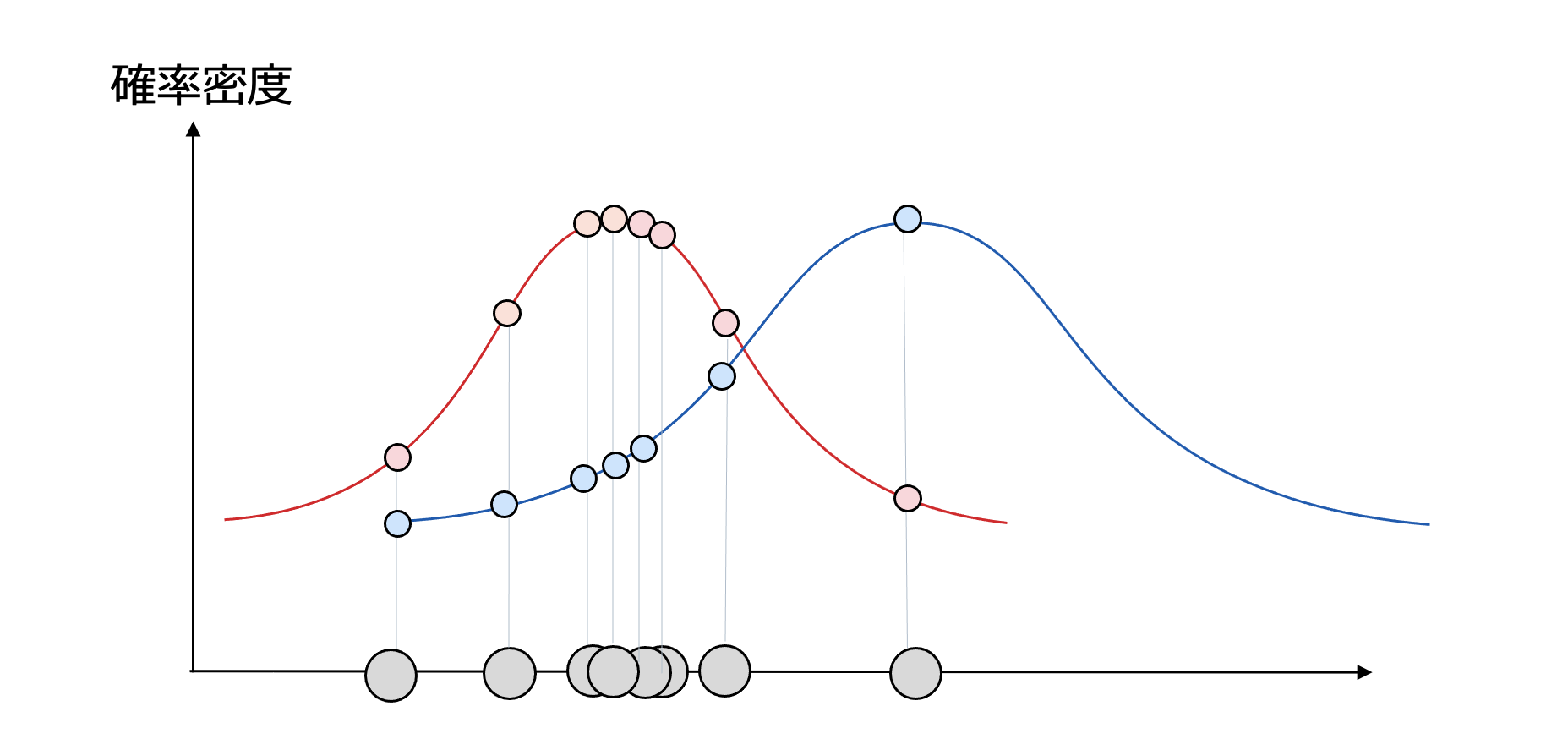
これを見る限りだと、赤の正規分布に合っていると皆さんは判断すると思います。
これは正しいです！
先ほど、正規分布から生じるデータは平均周りでデータが生じると説明しました。
逆に、データが与えられた時、データが集まっているあたりを平均とした正規分布に従っている可能性が高いと推測できそうです。
赤の正規分布がもっともらしいと考えて良いでしょう。

では、もっともらしさを値で判断するにはどうしましょうか？
先ほど、データが集まっているあたりを平均とした正規分布に従っている可能性が高いと推測できると言いました。データが集まっているあたりでは確率密度が高いですよね。
それは当然です、分布の確率密度が高いところでデータが観測されやすいからです。
なので、各データの確率密度を掛け合わせた値も高そうです。実際、赤と青で掛け合わせた確率密度を比較すると赤の分布のほうが大きくなることはわかると思います。
実は、この掛け合わせた値が大きいほど、データは分布に合っていると言えるのです。

正規分布での各データの確率密度を掛け合わせた値を尤度と呼ぶことにします。
尤度を使ってもっともらしさを判断できるのです！

尤度が大きいほど、データは分布に合っていると言いました。
実は、統計モデルがデータに合っているかどうかも、尤度をもとに判断できます。
そのことについて説明していきます。

この統計モデルでは真の値が直線上に並ぶと仮定したモデルで
真の値を平均とした正規分布に従って、データが得られることを想定しています。

このことから統計モデルを確率分布と考えて問題ないでしょう。
統計モデルはあるxの値が与えられた時の真の値を平均とした正規分布なのです。
先ほどのデータに合う正規分布を求めたのと同じアプローチが可能ですね。

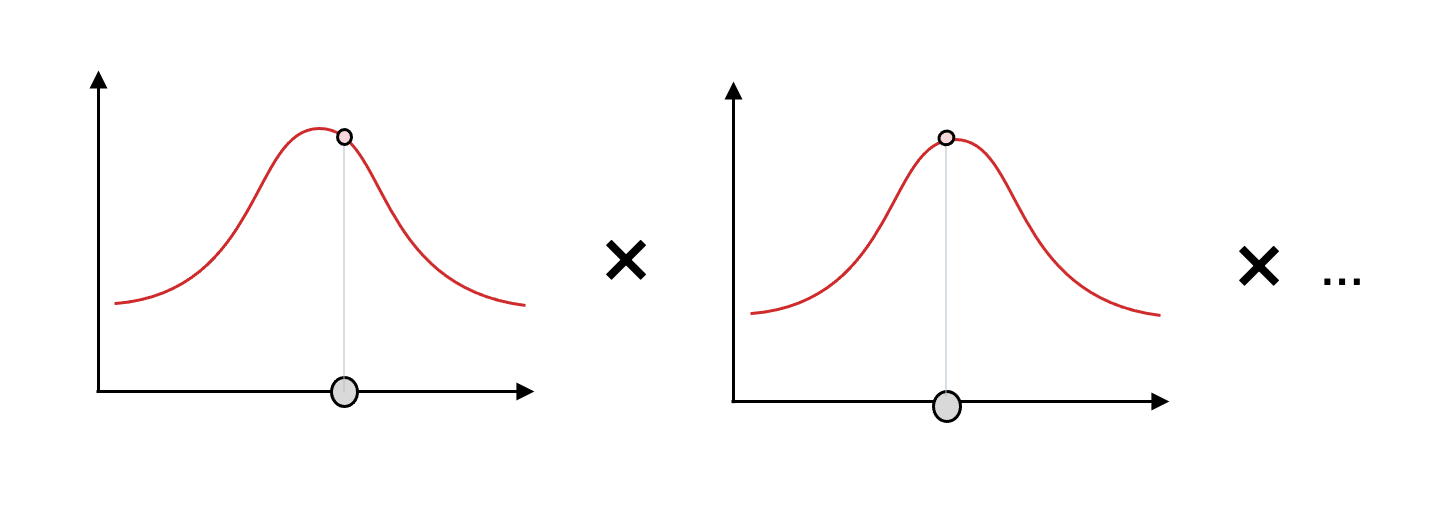
以上より、データのyの値は、真の値を平均とした正規分布に従っていると考えることができます。なので、次の図のように、各データごとに従っている正規分布から、データの確率密度が得られます。

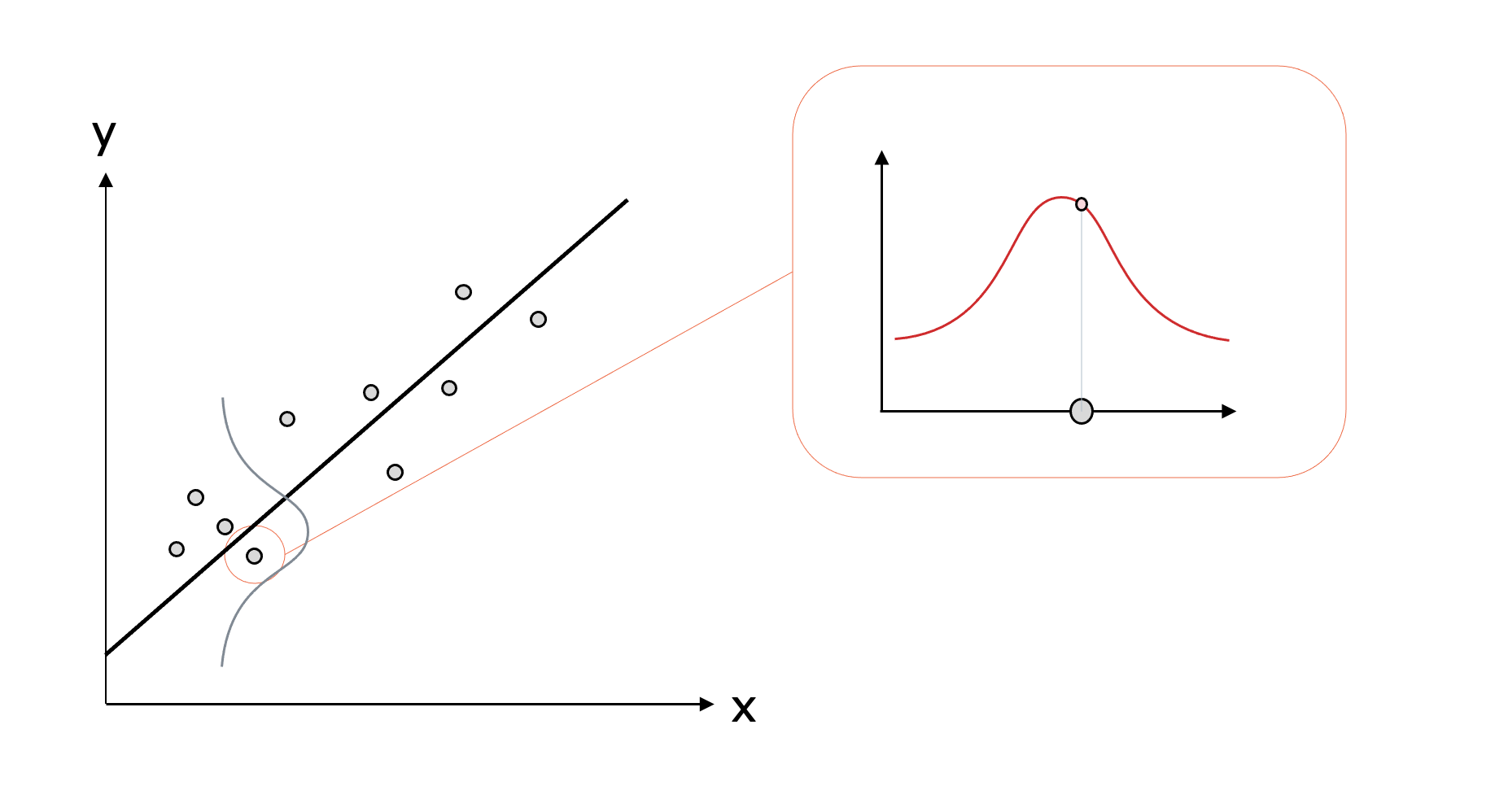
そして全てのデータに対して確率密度を掛け合わせると尤度が求められます。
尤度は0以下の値を掛け合わせて算出されるので掛け合わせるほど小さくなっていきます。そのため、対数をとることで掛け算は足し算になり小さい値でも見やすい値になります。尤度に対してlogで対数を取った値を対数尤度としましょう。
これ以降は尤度ではなく使い勝手のいい対数尤度を使っていきます。

このように対数尤度を比較することで、どのモデルがデータに合っているかを判断することができます！

次のように、データに対して３つのモデルを用意して対数尤度を求めて比較してみました。

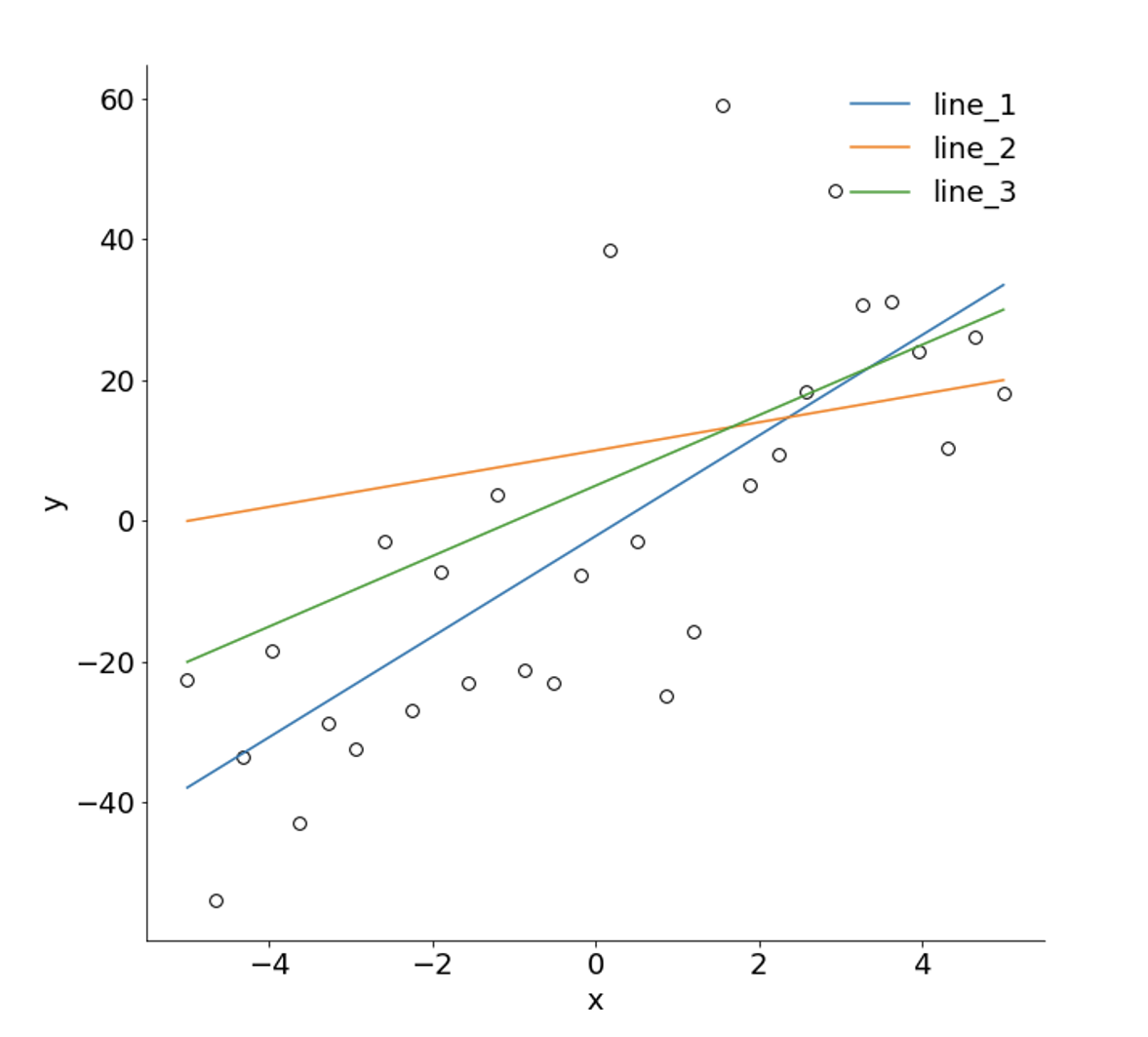
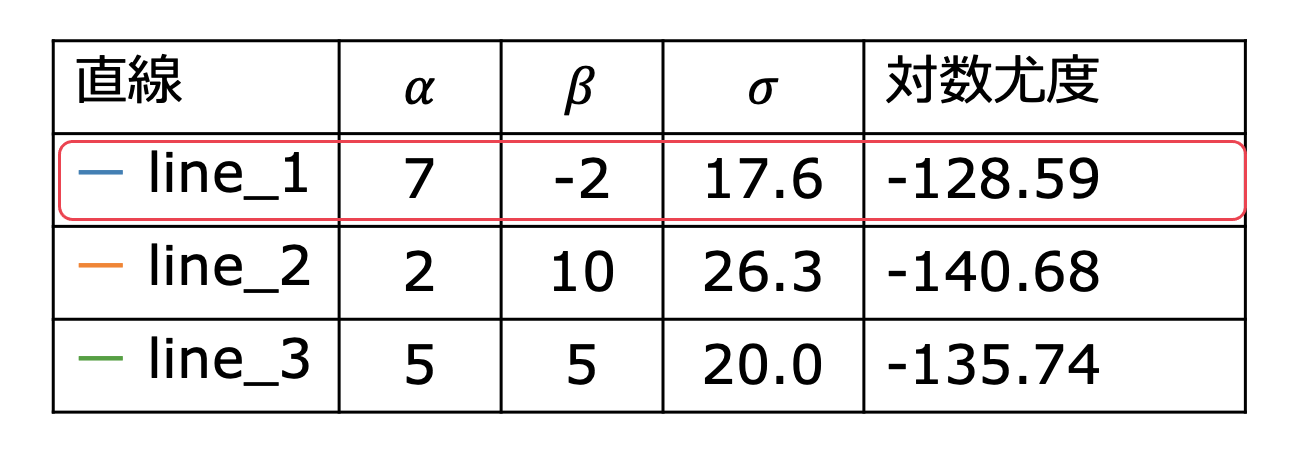
対数尤度が大きいほどデータに合っていると考えられるので
この3つのモデルの中でline_1が一番データに合っていることがわかりました。
感覚的にもline_1が一番データに合ってそうですよね。

今回の場合は3つのモデルを用意して対数尤度を比較しましたが
実は数学的に対数尤度の最大値のパラメータを求めることが可能です。
今回は、数式までは追いませんが、最大対数尤度のモデルを求めることを最尤推定と言います。

この記事では最尤推定についてこれ以上深く触れないので
最大対数尤度という値が大きければデータに合っているモデルなんだなという認識で大丈夫です。

さて、最大対数尤度のモデルがデータに合ったモデルなんだなということがわかりました。
しかし、それは仮定したモデルがデータに合っているということを意味しているだけで、仮定によって、いくつもモデルが考えられます。

例えば、次のような多項式回帰モデルが考えられます。

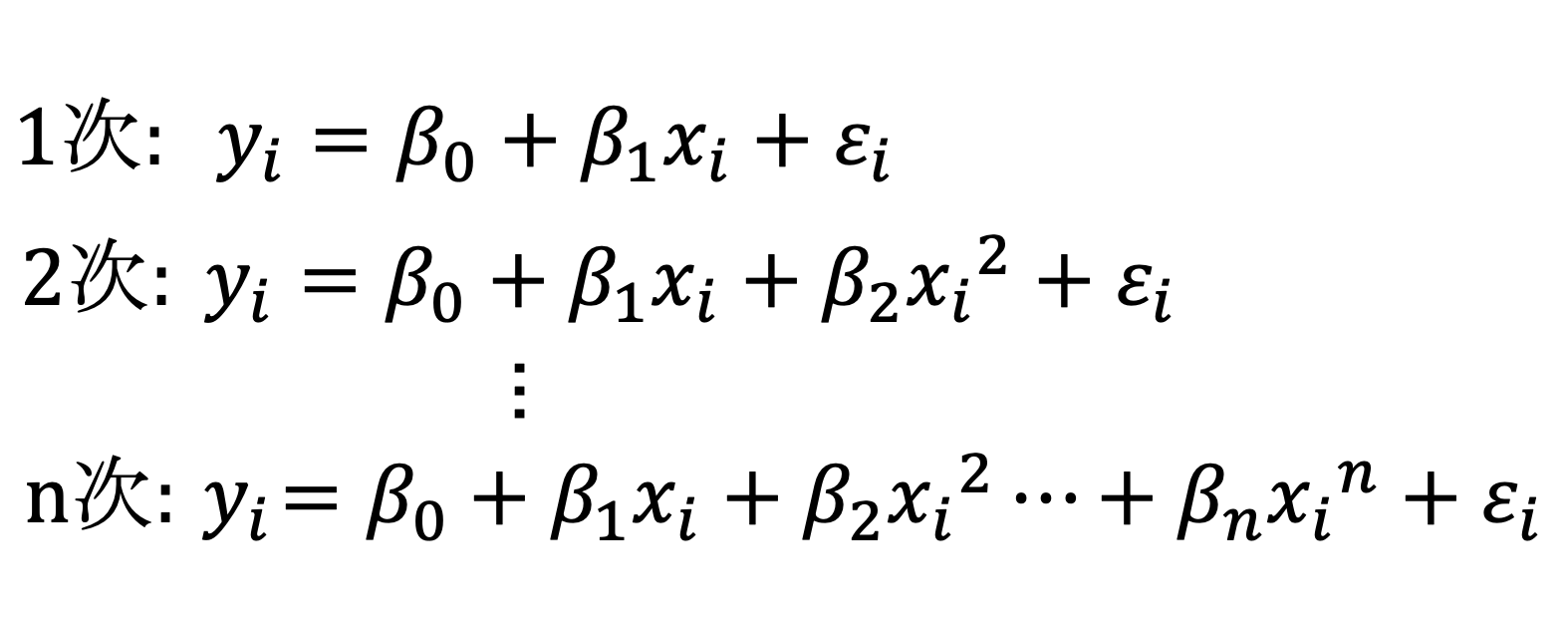
これは基本的に次数が増えるほど、表現の幅が広がりデータにピッタリ合うモデルを求めることが可能です。

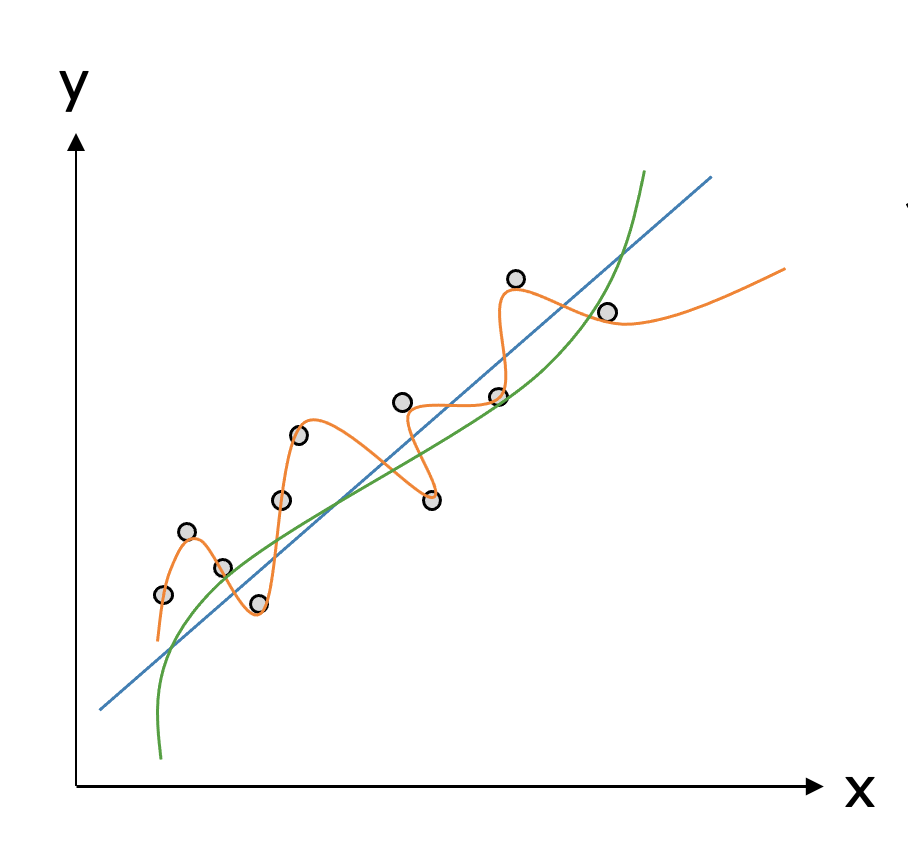
具体的に、多項式回帰モデルでの次数ごとに最大対数尤度を比較してみましょう。

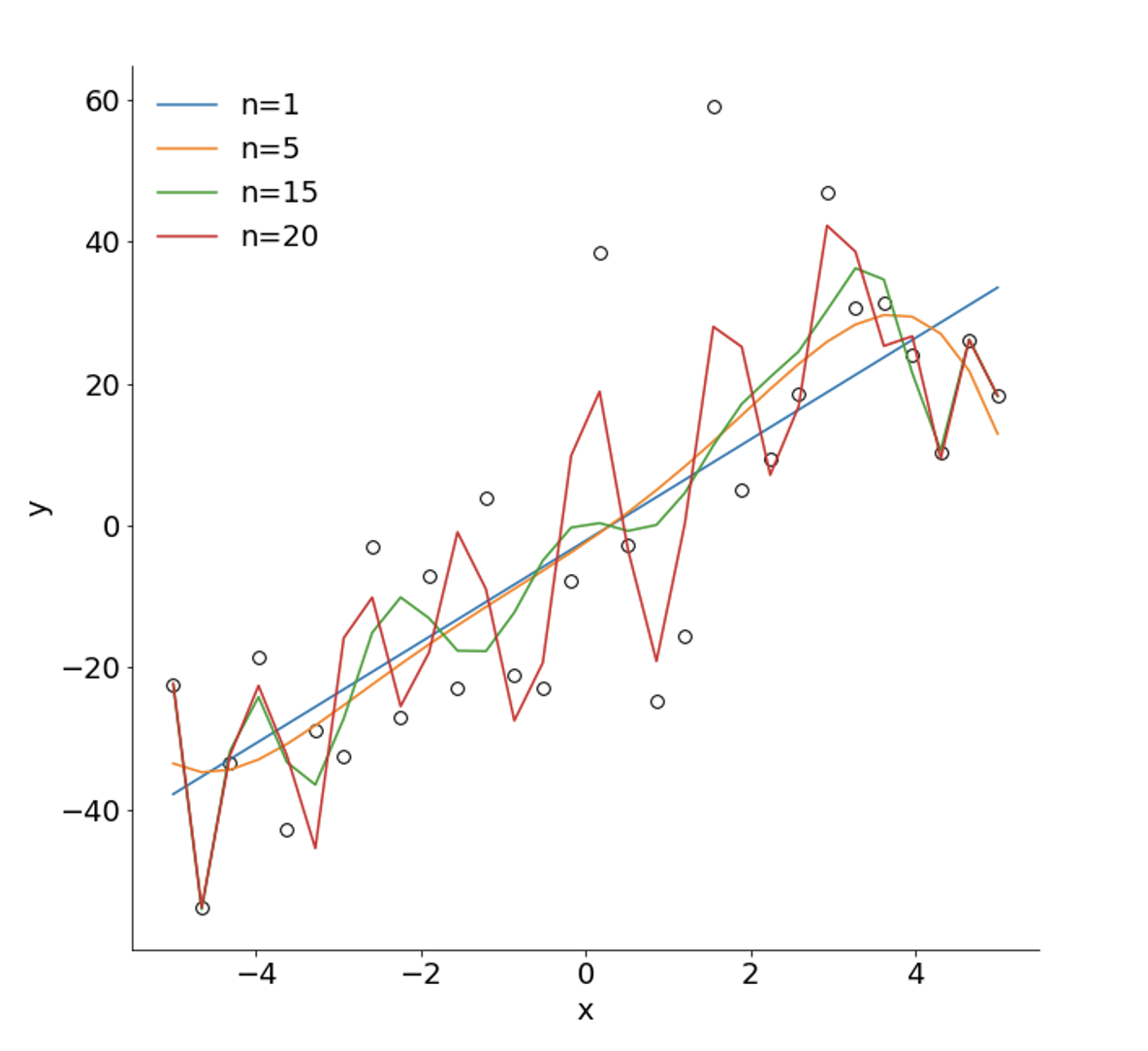
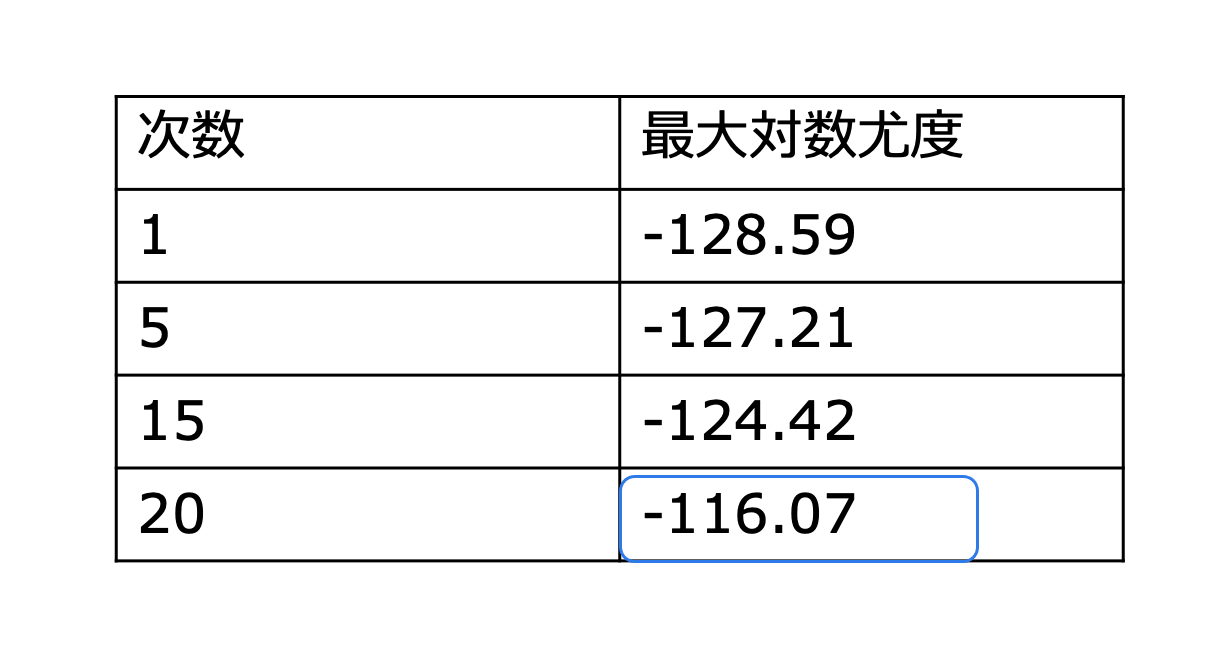
この結果を見てわかるように、次数が大きくなるほど最大対数尤度が大きくなり、データにピッタリ合うモデルとなっていることがわかりますね。

最大対数尤度が一番大きい、次数20はデータにかなり合っているモデルだと見てわかると思います。
しかし、データに合えば合うほど本当に良いモデルと言えるのでしょうか？
それについて考えていくことにしましょう。

良いモデルを考えるにあたって、データにピッタリあっているモデルの欠点をあげましょう。
次のように、今回観測したデータにはピッタリ合っているけれど、別で再度観測したデータや、もしかしたら得られたかもしれないデータなどには合ってない可能性があります。

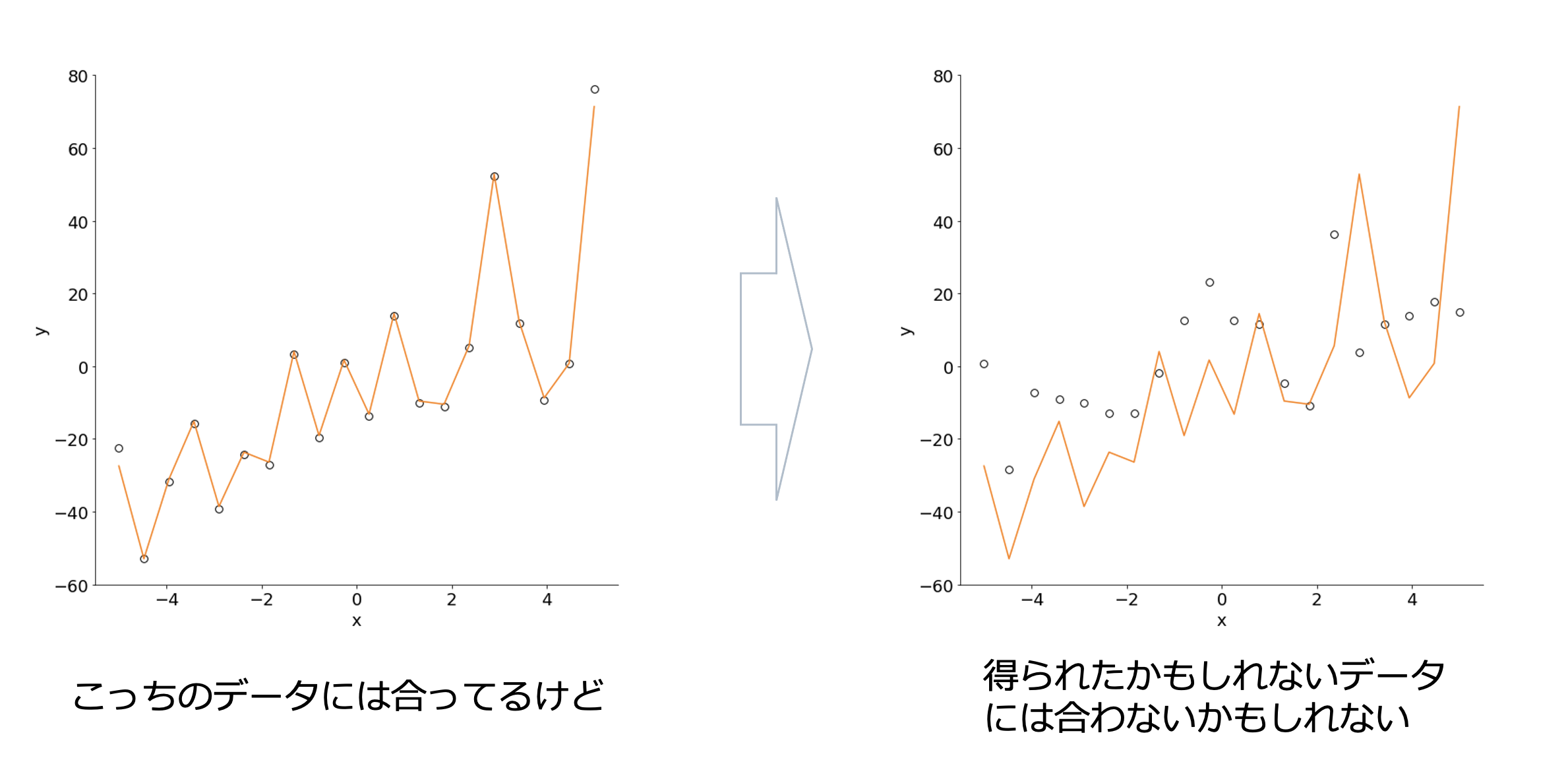
こういうモデルを現象の予測や分析するモデルとして役立てることができるでしょうか。

また次の例を見てみましょう。

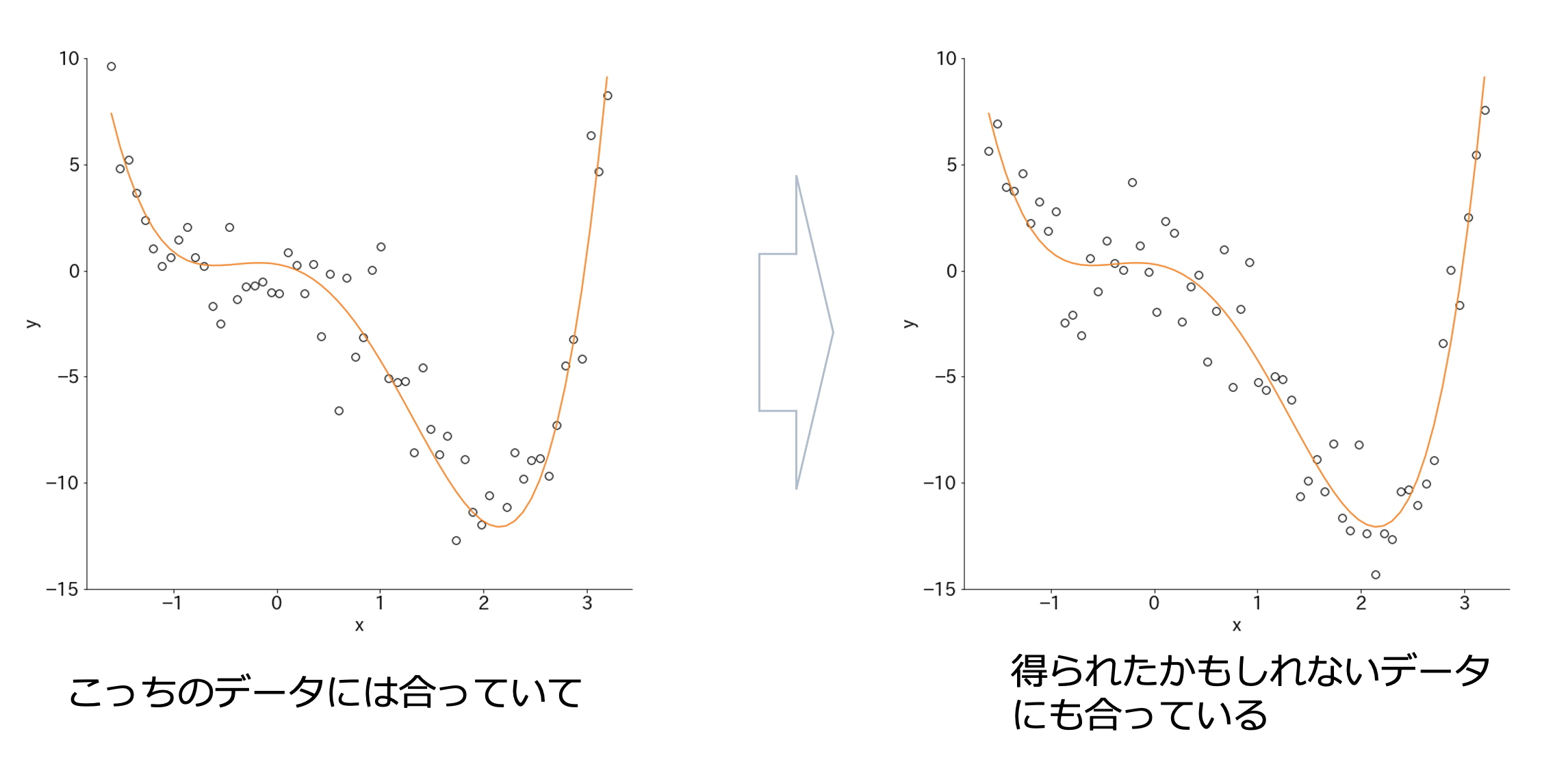
これは、観察されたデータにも合っていて、得られたかもしれないデータにも合っているモデルになっていると思います。
このモデルの方が先ほどのモデルよりも良いと思いませんか？

ここに良いモデルのヒントがあります。

再度、何のためにモデルを構築しているか考えみましょう。

データは現象の奥に潜む法則からバラツキをともなって現れたものでした。
そして真のモデルがあって、そこからデータが現れるはずです。
なので、真のモデルに近い統計モデルが良いということはわかると思います。

それでは、現実では得ることはできませんが真のモデルを仮定して少し実験をしてみましょう。
まずは、次のような真のモデルからデータをサンプリングしてみましょう。

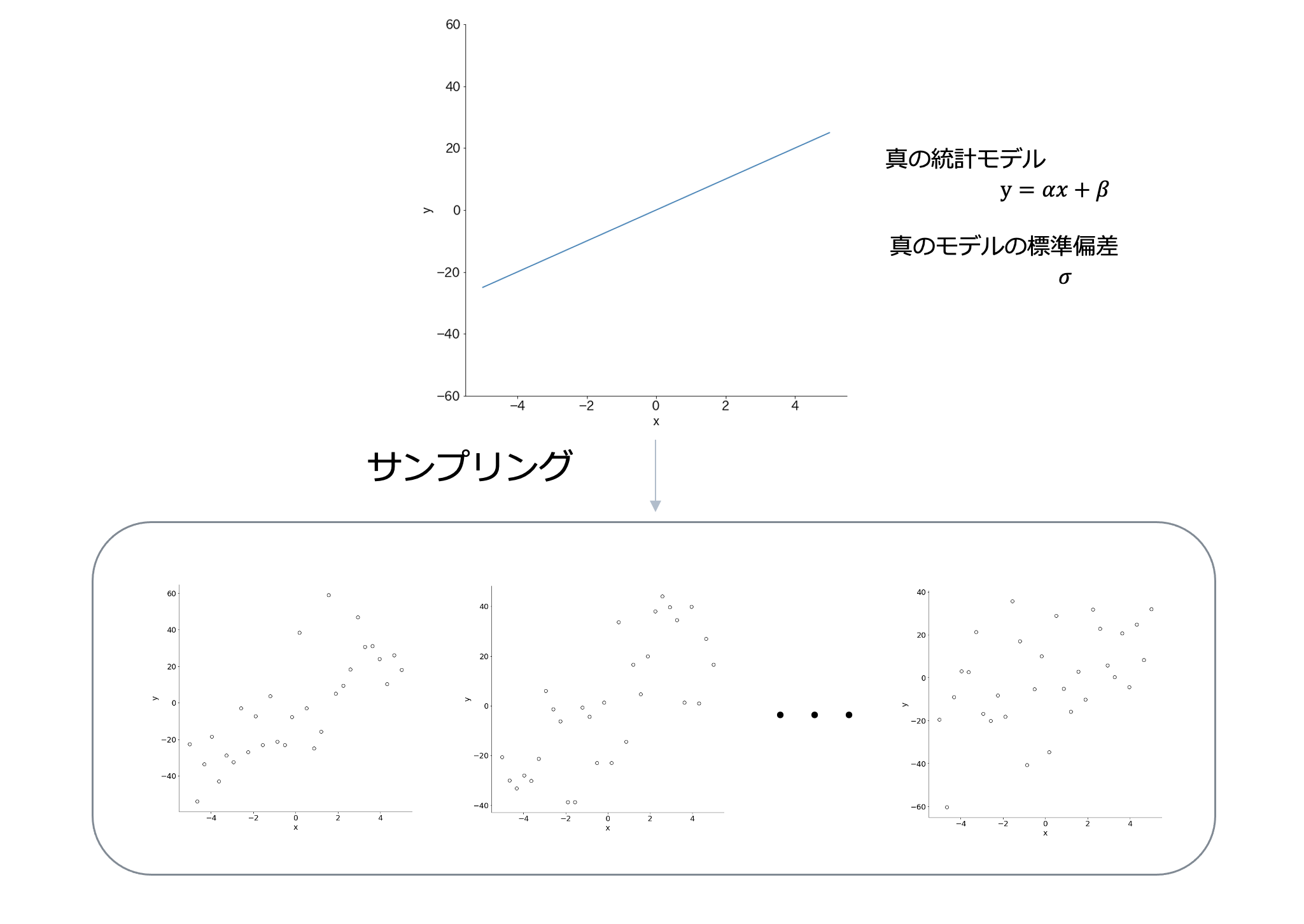
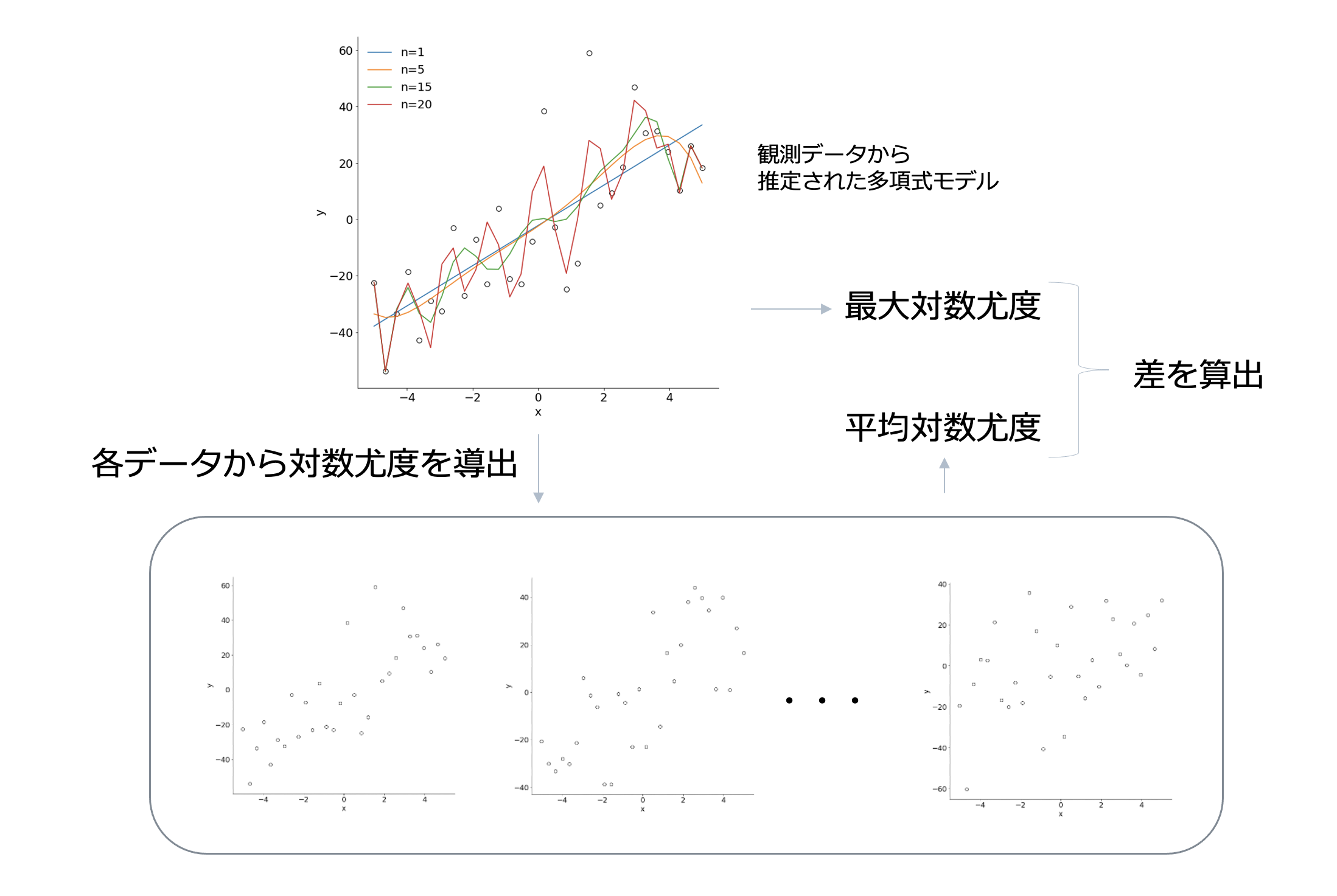
真の統計モデルからサンプリングしたデータに対して
真のモデルから観察されたデータから推定された多項式モデルで各データでの対数尤度を導出して、平均を求めてみます。

また、対数尤度の平均を取ったものを平均対数尤度と呼ぶことにしましょう。

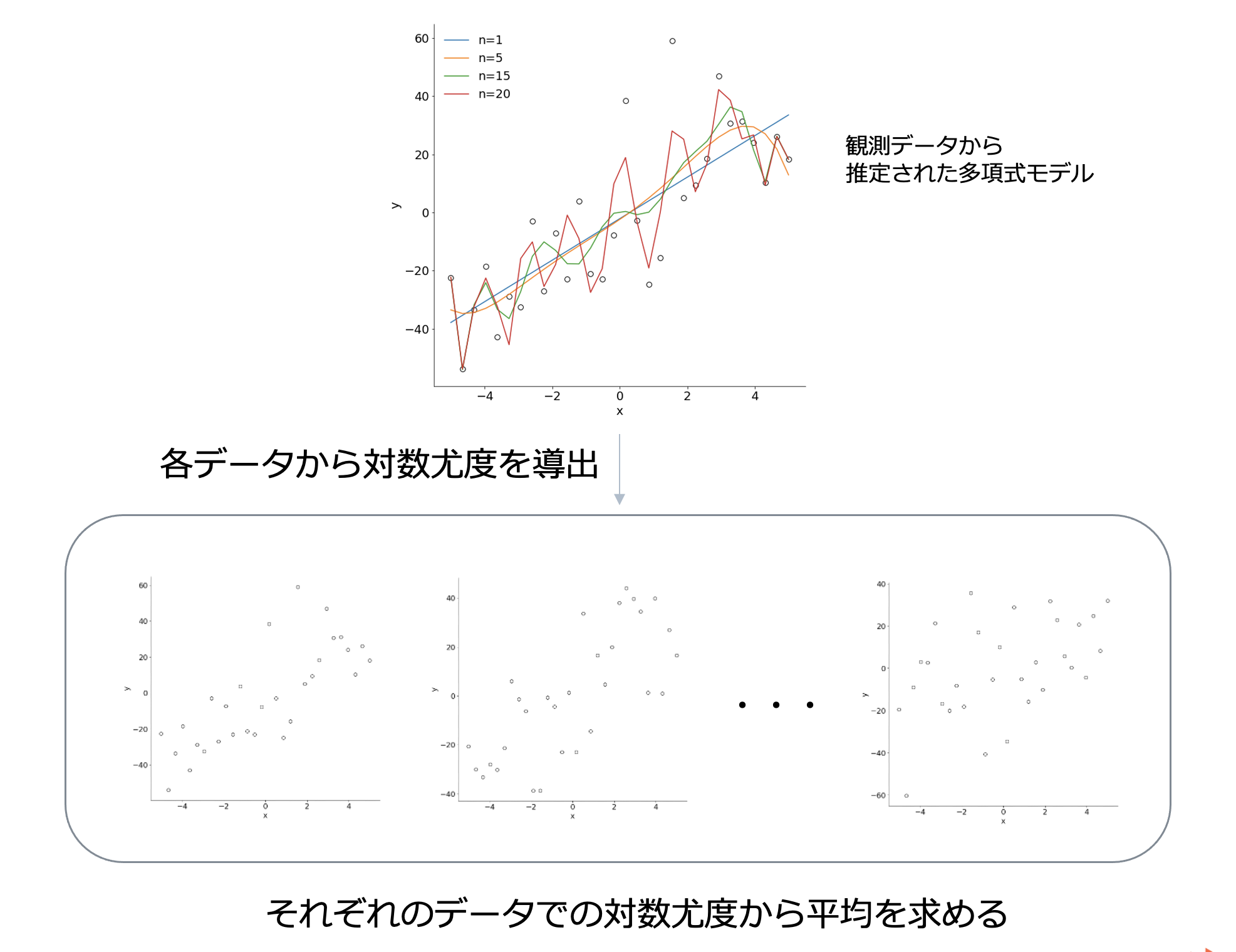
すると、次のような結果が得られます。

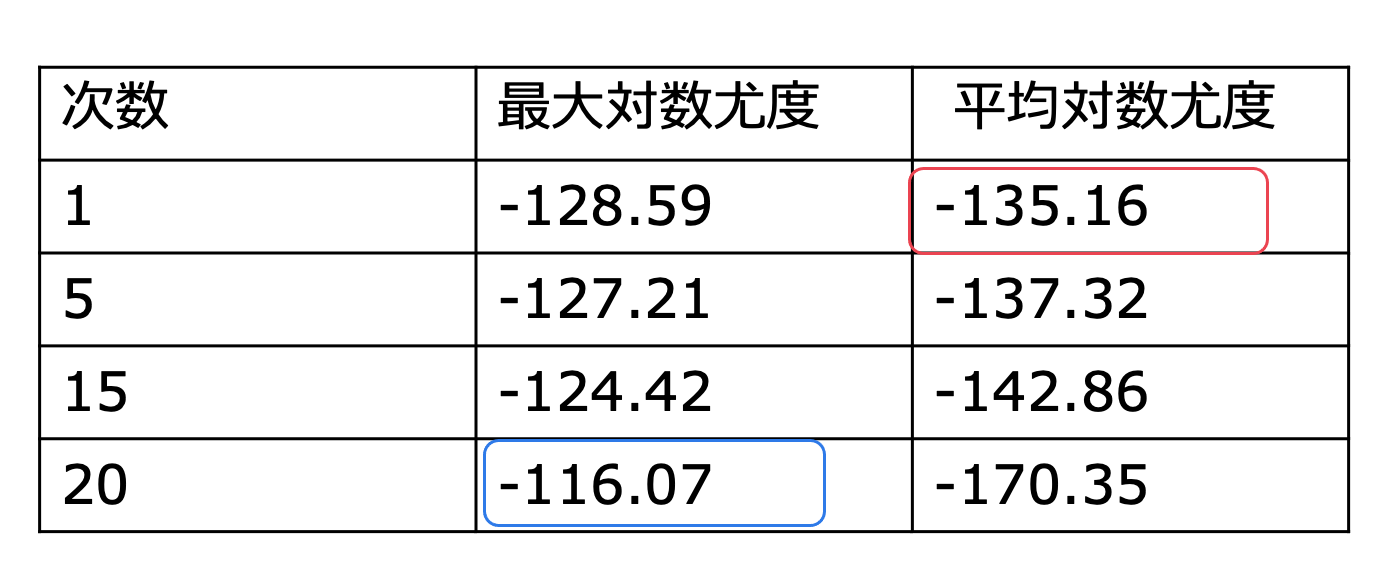
この時、真のモデルに一番近い、次数1の多項式モデルの平均対数尤度が一番大きくなっています。

平均対数尤度が大きいということは、それぞれのデータでの対数尤度が大きいことが多いということなので、どのデータに対しても合っている可能性が高いことを意味しています。

なので平均対数尤度の大きさは良いモデルの指標と考えたら良さそうです！

しかし、今回は真のモデルがわかっているので、観察データ以外のデータを得ることができましたが、本来は観察データ以外のデータを得ることはできません。
（現在のビッグデータ時代では大量にデータがある状態をイメージするかもしれません。確かに、大量のデータがあれば平均対数尤度を求めることは可能ですが、実用面ではデータが少ない場合の方が多いと思いますので、今回は少ないデータでも良いモデルを求める方法を考えることにします。）

観察データだけでモデルの良さを判断するにはどうすれば良いでしょうか？

実は、最大対数尤度とモデルのパラメータ数から次のように平均対数尤度の推定値を得ることができることが知られています。

また、この両辺に-2をかけると赤池統計量基準になります。便宜上-2をかけています。

赤池統計量基準は、平均対数尤度に-2をかけたものなので
赤池統計量基準の値が小さいほどモデルの予測の良さを表しています。

赤池統計量基準の導出が気になる方がいると思うのですが
導出過程だけで3つぐらい記事が書けてしまうボリュームになります。
赤池先生という偉い方が、数学を駆使してこの式を導出したと割り切る方がまずは良いかと思います。

導出が気になる方は「情報量統計学」の本をあたってみてください。
とても難しいので、ある程度、統計学や数学の知識がついてから読むことをおすすめします…。

さて、実際に最大対数尤度と平均対数尤度の差がパラメータ数になるのかを検証してみましょう。

まず、次のように先ほどの平均対数尤度の導出とほとんど同じ手順ですが、真のモデルからサンプリングしたデータに対して平均対数尤度を求め、モデルの最大対数尤度との差を取ることにします。

次の結果は、上の手順で４次多項式モデルでの最大対数尤度と平均対数尤度の差の導出を2000回繰り返してプロットしたものです。

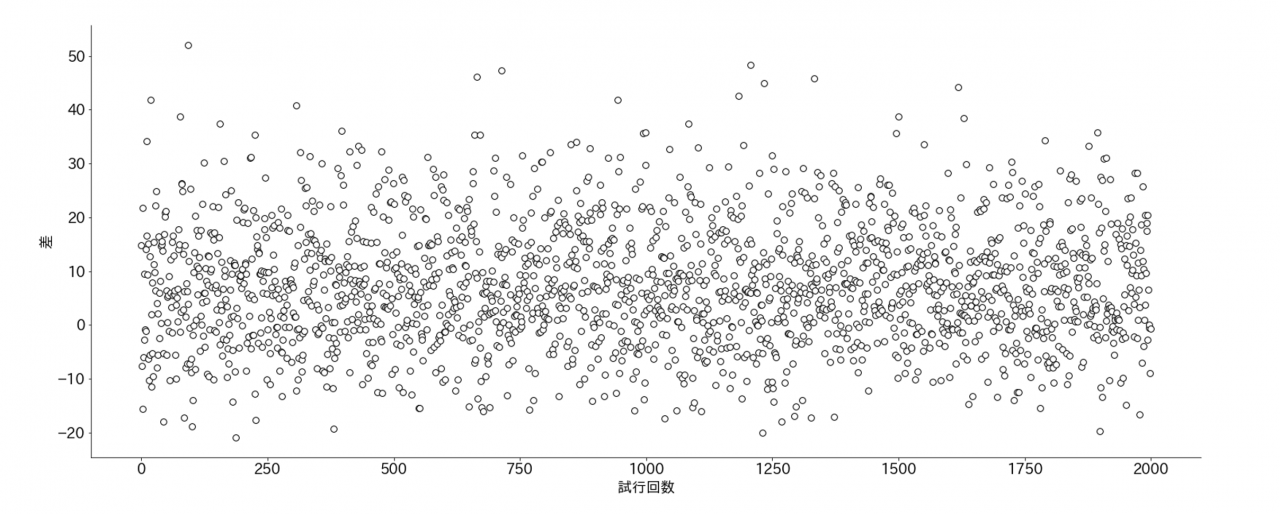
横軸が試行回数で、縦軸は差になります。
4次多項式回帰モデルの場合は、パラメータ数は6個になります。
差はパラメータ数になるはずなので、6であることが望ましいのですが、結果を見る限りでは、バラついていて、とても6とは言えません。
でもバラツキの真ん中あたりが６であるような気がしますよね。これは後で確かめてみましょう！

赤池統計量基準は、平均対数尤度との一致を保障するものではないことがわかります。あくまで推定値であってバラツキがあるものなんだなと理解しておく必要があります。
たまに一致すると考えている人がいるので注意が必要です。

さて、先ほどバラツキの真ん中あたりがパラメータ数であることを少し触れました。

なので、2000回繰り返して導出した差の平均をとって見てみましょう。
次のように1~6の次数のモデルでの差の平均をとってプロットしてみました。

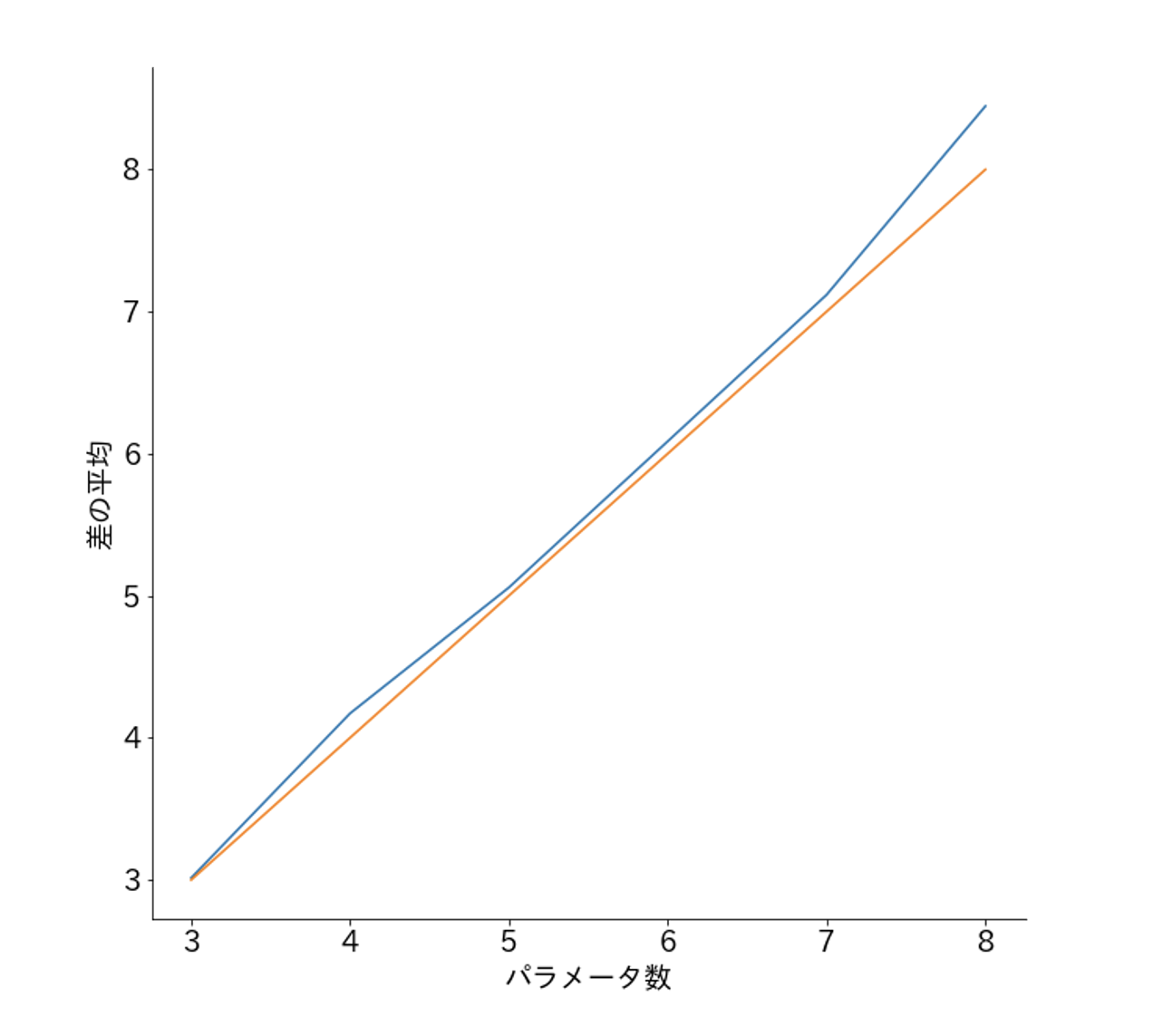
するとほとんどパラメータ数と差の平均が一致していることがわかります。

このように赤池統計量基準は本当に最大対数尤度と平均対数尤度の差がパラメータ数であることがわかりました。
実際にシミュレーションで確かめてみると感動します。理論が正しいのかきちんと自分の目で確かめると深い学びにつながるので皆さんもぜひやってみてください！

多項式回帰モデルで赤池統計量基準を求めてみましょう。
すると次のような結果になりました。

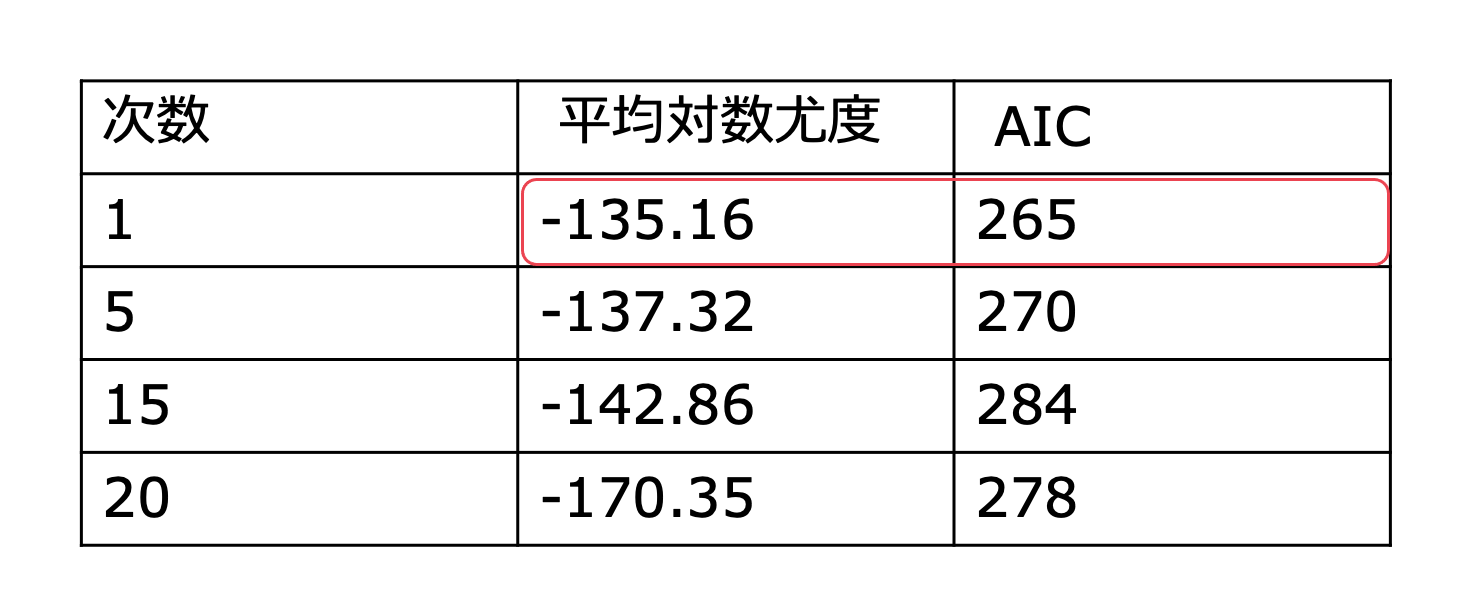
赤池統計量基準は小さいほど良いモデルなので次数1が一番良いモデルであると判断できます。
平均対数尤度は大きいほど良いモデルなので次数1が一番良く、結果が一致していますね。
ただし、赤池統計量基準はかなりバラツキがあるのでデータによっては平均対数尤度とはかなり異なる場合があり、正しいモデルを選択できないことがあります。

しかし、バラツキがあるにせよ観察データが限られている中で、平均対数尤度を推定できるのはすごい指標だなと私は思います。
実用的にも赤池統計量基準を利用することで良いモデルの判断する指標として、非常に優れていますよね。

統計学の視点から良いモデルとは何かをみてきました。

最後に、機械学習の深層学習との関わりに軽く触れて終わることにします。

深層学習の学習は簡単に言えば、学習用のデータに合うモデルを目指しています。これは最尤推定で、観察されたデータに合うモデルを求めているのと同様です。
実際、深層学習では学習時に損失関数を小さくするように学習していますが、この損失関数の最小値を求めることは最大対数尤度を求めることと同じことなのです。

しかし、最大対数尤度が他のデータに対して合うかはまた別の話だったように、損失関数の最小値を求めても他のデータに対して合うとは限りません。つまり、損失関数を小さくしすぎると過学習になることがあります。そこで、深層学習では、正則化やドロップアウトなど過学習になりすぎないような手法をたくさん編み出してきました。

このような過学習の抑制で何を目指しているかというと、平均対数尤度に近づけるようにしていると考えると少しスッキリするのではないでしょうか？

このように、統計学の視点から機械学習をを眺めることで、機械学習の少し曖昧な理解のところを数学的に理解できるようになると思います。

読んでいただきありがとうございました。