技術研究所のまつけんです。
先日、JDLA (日本ディープラーニング協会) のG検定 (ジェネラリスト検定) を受けてみました。恐らく合格しているとは思うのですが、少しばかり悔いの残る結果でした。というのも、途中で自宅のインターネット環境 (固定回線) が不調になり、5分くらいロスしてしまったからです。予め、スマホでテザリングできるようにスタンバイさせていた (古いPCも予備としてスタンバイさせていた) ので、どこかの段階でそちらに切り替えようかと思っていましたが、固定回線が復旧したので、テザリングへの切り替えはせずに済みました。トラブルに備えてPCと回線は二重化しておくと安心ですね。
さて、先日の記事で(あ)がデジタル画像についての話をしました。その中で「三原色」について触れていましたが、今日は、その「三原色」について詳しく説明したいと思います。
人間の目は、どのようにして色を識別しているのでしょうか? それについて学ぼうとすると、「等色関数」に出会います。グラフや数式を使った説明は、Wikipediaなどに載っています[1]。3つのそっくりな式が登場しますが、たいてい、この式の意味が腹落ちするのに結構な時間を費やしてしまうかと思います。かくいう私も腹落ちするまでに1週間ほど掛かってしまいました。
こういった物理現象の説明というのは適切な比喩 (業界用語でメタファ metaphor といいます) を思いつくと簡単に腹落ちするものです。今日は、この数式について、私が理解するときに考えた比喩を紹介したいと思います。
まず最初に「波長による積分(∫・dλ)」を「波長ごとの総和(Σ)」に変換します。積分は細かく区切ることで総和の計算で近似できます。詳しくはWikipediaに載っています[2]ので説明は省略します。
3つの数式
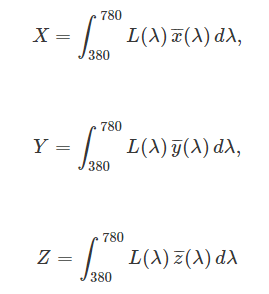
は
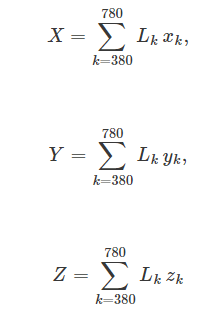
のように書き直せます (積分と総和の範囲が380から780までになっているのは、人間の目に見える光の波長が380から780ナノメートルだからです)。さて、これらの式は、どういった意味でしょうか? より一般的に書けば
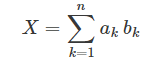
のようになります。実は、この式は多くの人が毎日、日常生活の中で行っている計算です。例えば、

つまり、
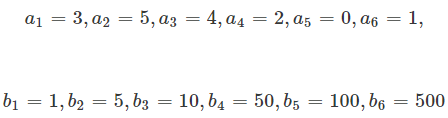
のとき、 Xは668となります。これは、「1円玉3枚、5円玉5枚、10円玉4枚、50円玉2枚、100円玉0枚、500円玉1枚」の合計の価値が668円である、という計算をしていることになります。このように、aにそれぞれのコインの枚数を、bにそれぞれのコインが持つ価値を入れれば、
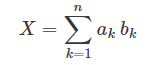
で合計の価値が計算できるわけです。
では、話を
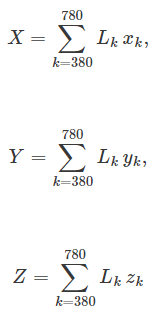
に戻しましょう。ここではコインではなく、ベースボールカード (野球選手のトレーディングカード) と3人のコレクターを例に説明します。
あなたは手元に数千枚のコレクションを持っています。そして、近所にxさん、yさん、zさんという3人のコレクターが住んでいます。そして、この3人は異なる価値観を持っています。
例えば、あなたは背番号380番の選手のカードを15枚持っています。xさんは、そのカードを1枚10円で買い取りたいと思っていますが、yさんは5円しか出したくないし、zさんは1円しか出したくないと思っています。この事実を
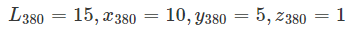
と記述します。このように、380番から780番までのカードのそれぞれについて、あなたの保有枚数、xさんの買い取り価格、yさんの買い取り価格、zさんの買い取り価格がわかっていれば、先程の式で計算されるXは、自分のコレクションをすべてxさんに買い取ってもらう場合の合計の金額ということになります。同様に、YとZは、それぞれ、yさんとzさんに買い取ってもらう場合の合計金額となります。
つまり、人間の目の中には価値観の異なる3種類の人が住んでいて、それぞれの人が出した数値によって見える色が決まる、と考えれば良いわけです。なお、人間は3種類 (3色型色覚) ですが、犬や猫などは2種類 (2色型色覚)[3]、爬虫類や鳥類などは紫外線も見える4種類 (4色型色覚) のようです[4]。4色型色覚では、どんな風に世界が見えているんでしょうね。




