技術研究所のまつけんです。
先日、新しい趣味を始めました。「大回り乗車」です。これは「大都市近郊区間内のみを利用する場合の特例」(都市部に限り、実際の乗車距離ではなく、最短の距離で運賃を計算する (ただし、同じ駅を2回以上通ることはできない) という特例)を利用して、安い料金で長距離を移動してしまおうというものです。
例えば、東京駅から総武線で西船橋駅に行き、武蔵野線で西国分寺駅に出て、中央線で神田駅まで戻ってきても、改札から一度も出なければ、東京-神田間の料金140円しか掛かりません。改札から外に出ることは出来ませんが、車窓の風景を楽しむことが出来ますし、エキナカで食事や買い物をすることは出来ます。詳しいことは、Googleなどで「大回り乗車」を検索すると色々と出てきますので、そちらを参照していただければと思います。
例えば、各都市近郊の大回り乗車用の路線図などは、こちらのサイトに掲載されています:
http://noritetsu.net/omawari/2015/03/sozai-download/
東京近郊の路線図を見ますと、一見しただけで、様々なルートで大回り乗車が楽しめそうだということがわかるかと思います。
さて、そういったものを見かけますと、大回り乗車のルートを列挙するプログラムを書いてみようかな、と思ってしまうのがソフトウェアエンジニア魂というもの(パズルを見ると、パズルを「解く」のではなく、「パズルを解くプログラムを作り」たくなる派なので)。というわけで早速、作ってみました。まずは、以下のような比較的単純な路線図を考えてみます:
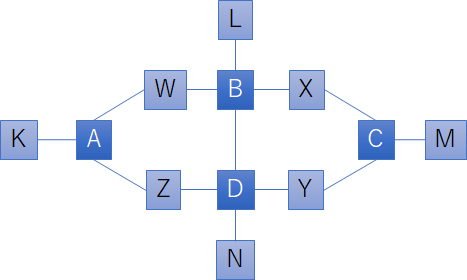
この路線図をコンピュータが解釈できる形式にしなければなりません。こういった路線図のようなものは、数学的には、グラフ graph といいまして、それを扱う学問をグラフ理論 graph theory といいます[1]。グラフ理論をコンピュータで扱うには、隣接行列 adjacency matrix を使うのが一般的です。
なお、今回の題材では、W駅は乗り換えの余地が無いので省略することが出来ます。同様に、X駅、Y駅、および、Z駅を省略することが出来ます。また、同じ駅を2回以上、通ることが出来ないことから、K駅、L駅、M駅、および、N駅も省略することが出来ます。すると、以下のように簡略化した路線図を考えれば良いことになります:
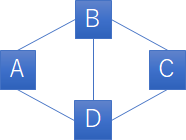
B駅からA駅またはC駅を経由してD駅に至る直通の列車がある場合に、A駅とC駅も乗り換えの余地が無い駅になりますが、B駅からD駅に至るルートが3通りあることを表現するためにA駅とC駅は残します。
この路線図を隣接行列として表すと、以下のようになります:
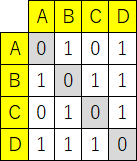
一部のモノレールなどを除き、鉄道は双方向に移動できます(A駅からB駅に行けるのであれば、B駅からA駅にも行ける)ので、今回の題材は無向グラフ undirected graph です。よって、対角成分(灰色の部分)に対して線対称になります。なお、A駅からどこも経由せずにA駅に戻るような路線は普通は無いので対角成分はすべてゼロとなります。
経路を探索する C++ のプログラムは、再帰呼び出しを使うことで、以下のように記述できます:
| #include <algorithm> |
| #include <iostream> |
| #include <string> |
| #include <vector> |
| using namespace std; |
| void search_routes( |
| const vector<vector<int>> & matrix, |
| const int n, |
| vector<int> route, |
| vector<vector<int>> & routes |
| ) { |
| if ((2 < route.size()) && (route[0] == n)) { |
| route.push_back(n); |
| routes.push_back(route); |
| return; |
| } |
| if ((0 < route.size()) && (route[route.size() - 1] == n)) { |
| return; |
| } |
| if (find(route.begin(), route.end(), n) != route.end()) { |
| return; |
| } |
| route.push_back(n); |
| for (int i = 0; i < (int)matrix[n].size(); i++) { |
| if (0 < matrix[n][i]) { |
| search_routes( |
| matrix, |
| i, |
| route, |
| routes); |
| } |
| } |
| } |
| int main(void) |
| { |
| vector<string> names; |
| vector<vector<int>> matrix; |
| names = { "A", "B", "C", "D" }; |
| matrix.push_back(vector<int>{ 0, 1, 0, 1 }); |
| matrix.push_back(vector<int>{ 1, 0, 1, 1 }); |
| matrix.push_back(vector<int>{ 0, 1, 0, 1 }); |
| matrix.push_back(vector<int>{ 1, 1, 1, 0 }); |
| vector<int> route; |
| vector<vector<int>> routes; |
| for (int i = 0; i < (int)names.size(); i++) { |
| search_routes(matrix, i, route, routes); |
| } |
| for (auto route : routes) { |
| for (int n : route) { |
| cout << names[n] << ","; |
| } |
| cout << endl; |
| } |
| return 0; |
| } |
実行結果は、このようになります:
| $ g++ test.cpp |
| $ ./a.out |
| A,B,C,D,A, |
| A,B,D,A, |
| A,D,B,A, |
| A,D,C,B,A, |
| B,A,D,B, |
| B,A,D,C,B, |
| B,C,D,A,B, |
| B,C,D,B, |
| B,D,A,B, |
| B,D,C,B, |
| C,B,A,D,C, |
| C,B,D,C, |
| C,D,A,B,C, |
| C,D,B,C, |
| D,A,B,C,D, |
| D,A,B,D, |
| D,B,A,D, |
| D,B,C,D, |
| D,C,B,A,D, |
| D,C,B,D, |
| $ |
各行は出発駅、経由駅、終着駅を並べたものになっています。例えば、「A,B,C,D,A,」は、A駅を出発して、B駅→C駅→D駅の順に経由して、A駅に戻るルートを表します。ただし、大回り乗車においては、同じ駅を通ったり、出発駅に戻ってきたりすることは出来ないルールなので、「A,B,C,D,A,」は「A,B,C,D,Z,」に読み替える必要があります。
如何でしたか? 次回は、実際の路線図を元に経路を探索してみたいと思いますので、お楽しみに。
(→ 鉄道とグラフ理論(2))




