昨年に引き続き[PR]データ分析やっていますと言いながらも、Tableauを使用したダッシュボード開発のプロジェクトに参画しています。
が、Rを使った分析プロジェクトも少しずつ増えてきています。なので今回はR+αの話でブログを書きたいと思います。
本当はTableau+Rによる記事を描きたかったのですが、どうやらRにデータを渡すためには一度SUMなどの集約関数を使用しないといけないようなので、ちょっと当初の目論見から外れてしまったため、今回の記事はちょっと趣向を変えていくつか出ているBIツール等との比較記事を書いてみました。
本題の前に、突然ですが、「シンプソンのパラドックス」についてご存知でしょうか?
私自身、このキーワードを最近知った(参考文献.1)のですが、Wikipedia:シンプソンのパラドックス(2018年12月中旬の本記事執筆時)によると、
母集団での相関と、母集団を分割した集団での相関は、異なっている場合がある。つまり集団を2つに分けた場合にある仮説が成立しても、集団全体では正反対の仮説が成立することがある。
とのことです。
西内(2013)の「統計学が最強の学問である」の書籍の中でもこういった言及があります。
A校とB校の同じ学年の生徒に対して同じ模擬試験を受験させた。
男子生徒同士で比べるとA校の平均点はB校よりも5点高い。
女子生徒同士で比べるとA校の平均点はB校よりも5点高い。
A校とB校の平均点を全体で比較するとB校の平均点はA校よりも4点高かった。
※本書の中では層別解析でパラドックスは防げるものの、層の観点が増えてしまうと大変であるということで重回帰分析を勧めています。
シンプソンのパラドックスを回避する策等については本記事では言及はしませんが、つまるところ、「データの解釈をする際に、切り取る視点によって全く逆のことが言えてしまうことがある」ということのようです。
とはいえ、シンプソンのパラドックスを言葉で説明されても、漠然としているのではないでしょうか。ということで、実際にグラフを描いて確認してみたいと思います。また、今回はいくつかの手段で可視化を試みたいと思います。
こちらです(最初の10件のみ表示しています)。表にするとこのような形になります。
| NO | 学校 | 性別 | 得点 |
|---|---|---|---|
| 1 | A校 | 男性 | 45 |
| 2 | A校 | 男性 | 63 |
| 3 | A校 | 男性 | 55 |
| 4 | A校 | 男性 | 68 |
| 5 | A校 | 男性 | 60 |
| 6 | A校 | 男性 | 66 |
| 7 | A校 | 男性 | 64 |
| 8 | A校 | 男性 | 71 |
| 9 | A校 | 男性 | 46 |
| 10 | A校 | 男性 | 56 |
学校列はA校/B校、性別列は男性/女性、得点列は100点満点のデータです。
これらは前述の西内(2013)の数字になるように下記のRで乱数を発生させています。微妙に端数が合わず、全体の平均がそろわなかったので、その後意図的にデータを手で調整しています。あまりスマートではなくスミマセン。
| library(dplyr) |
| library(tibble) |
| # 平均値、分散を指定していい感じに作る |
| a_male <- round(rnorm(n = 160, mean = 60, sd = 10), 0) |
| a_female <- round(rnorm(n = 40, mean = 75, sd = 10), 0) |
| b_male <- round(rnorm(n = 40, mean = 55, sd = 10), 0) |
| b_female <- round(rnorm(n = 160, mean = 70, sd = 10), 0) |
| # その後、四捨五入しているので結局、微調整を手でしています。 |
| a_male <- c( |
| 45, 63, 55, 68, 60, 66, 64, 71, 46, 56, |
| 71, 60, 42, 46, 53, 68, 72, 56, 64, 46, |
| 47, 66, 65, 55, 55, 49, 66, 60, 44, 64, |
| 60, 60, 34, 66, 63, 58, 62, 45, 66, 66, |
| 60, 64, 53, 58, 69, 59, 65, 55, 58, 57, |
| 76, 56, 67, 56, 76, 34, 53, 67, 49, 63, |
| 59, 44, 53, 63, 48, 59, 60, 66, 53, 58, |
| 40, 49, 56, 63, 57, 55, 74, 58, 61, 68, |
| 74, 63, 64, 68, 77, 49, 69, 69, 63, 56, |
| 67, 54, 49, 79, 60, 62, 63, 71, 71, 57, |
| 56, 70, 81, 81, 58, 57, 54, 69, 64, 70, |
| 56, 62, 66, 85, 63, 75, 59, 68, 65, 57, |
| 59, 69, 91, 78, 59, 60, 55, 48, 52, 55, |
| 52, 57, 70, 70, 58, 45, 49, 61, 46, 64, |
| 50, 57, 71, 65, 47, 69, 59, 72, 49, 54, |
| 71, 33, 61, 66, 53, 49, 47, 61, 57, 48) |
| a_female <- c( |
| 80, 73, 92, 98, 75, 72, 65, 72, 62, 63, |
| 83, 90, 82, 77, 79, 70, 73, 87, 72, 76, |
| 70, 76, 82, 72, 67, 68, 71, 54, 78, 74, |
| 90, 91, 74, 64, 63, 74, 77, 89, 63, 62) |
| b_male <- c( |
| 56, 64, 61, 60, 53, 66, 65, 51, 50, 54, |
| 50, 52, 51, 59, 59, 52, 61, 72, 42, 55, |
| 42, 58, 49, 59, 60, 36, 75, 48, 34, 64, |
| 53, 62, 46, 60, 47, 54, 59, 49, 55, 57) |
| b_female <- c( |
| 90, 80, 62, 73, 60, 76, 75, 68, 82, 82, |
| 67, 79, 71, 81, 54, 82, 65, 77, 71, 61, |
| 62, 76, 71, 76, 62, 90, 55, 64, 83, 92, |
| 66, 90, 71, 66, 80, 57, 63, 65, 71, 62, |
| 55, 52, 68, 72, 79, 81, 76, 65, 65, 76, |
| 75, 85, 74, 60, 59, 67, 63, 64, 81, 84, |
| 81, 81, 55, 76, 80, 69, 84, 57, 78, 72, |
| 63, 72, 82, 79, 58, 73, 52, 57, 58, 69, |
| 73, 70, 83, 76, 58, 92, 65, 65, 65, 59, |
| 80, 78, 68, 61, 64, 78, 62, 69, 81, 65, |
| 91, 79, 68, 74, 68, 67, 81, 83, 67, 92, |
| 67, 84, 75, 67, 67, 53, 62, 55, 68, 74, |
| 65, 77, 75, 70, 68, 56, 74, 60, 65, 61, |
| 54, 69, 68, 71, 67, 62, 66, 80, 69, 74, |
| 69, 59, 69, 79, 69, 64, 67, 56, 66, 78, |
| 85, 83, 53, 56, 56, 80, 53, 55, 70, 53) |
| # 表を作る関数 |
| create_table <- function(male, female, school){ |
| table_male <- tibble::tibble(male) %>% |
| dplyr::rename(得点 = male) %>% |
| dplyr::mutate(性別 = "男性") |
| table_female <- tibble::tibble(female) %>% |
| dplyr::rename(得点 = female) %>% |
| dplyr::mutate(性別 = "女性") |
| return(dplyr::bind_rows(table_male, table_female) %>% |
| dplyr::mutate(学校 = school)) |
| } |
| # A校とB校をユニオンする |
| data <- dplyr::bind_rows( |
| create_table(a_male, a_female, "A校"), |
| create_table(b_male, b_female, "B校") |
| ) %>% |
| dplyr::select(学校, 性別, 得点) |
| # データの保存は省略 |
クロス集計してみると下記になります。
| 学校 | 区分 | 男性 | 女性 | 全体 |
|---|---|---|---|---|
| A校 | 人数 | 160 | 40 | 200 |
| 平均点 | 60 | 75 | 63 | |
| B校 | 人数 | 40 | 160 | 200 |
| 平均点 | 55 | 70 | 67 |
この表を見ると上記と引用部分と同じように男女それぞれで、A校がB校よりも5点高いものの、全体ではB校がA校よりも4点高いことがわかりますね。
それではここからデータの可視化をしていきたいと思います。タイトルの通り、ExcelとBIツール2種(Power BI & Tableau Desktop)を利用したグラフ、そして最後にRによるggplot2パッケージを利用したグラフを作ってみたいと思います。
作るイメージとしてはデータのばらつきをみたいので散布図のようなものを学校別、性別に分けることになります。
上記のデータを再び確認していただくとわかりますが、学校、性別は尺度でいうところの名義尺度(Tableauならディメンション、不連続データ)、得点は比例尺度(Tableauならメジャー、連続データ)となっています。このデータを可視化する際には不連続 × 連続のデータを可視化することになります。
使用するグラフのモジュールによってはこの不連続 × 連続のフォーマットに対応していない場合にちょっと工夫が必要になってきます。その場合はその都度補足をしたいと思います。
説明不要のマイクロソフト社のエクセルですね。メニューの挿入でグラフを作成して行きます。
エクセルでは軸を自動で指定して分割して表を作ってくれないため、いきなりですが散布図のY軸に得点、X軸に学校、系列に性別を指定して作成することになりました。
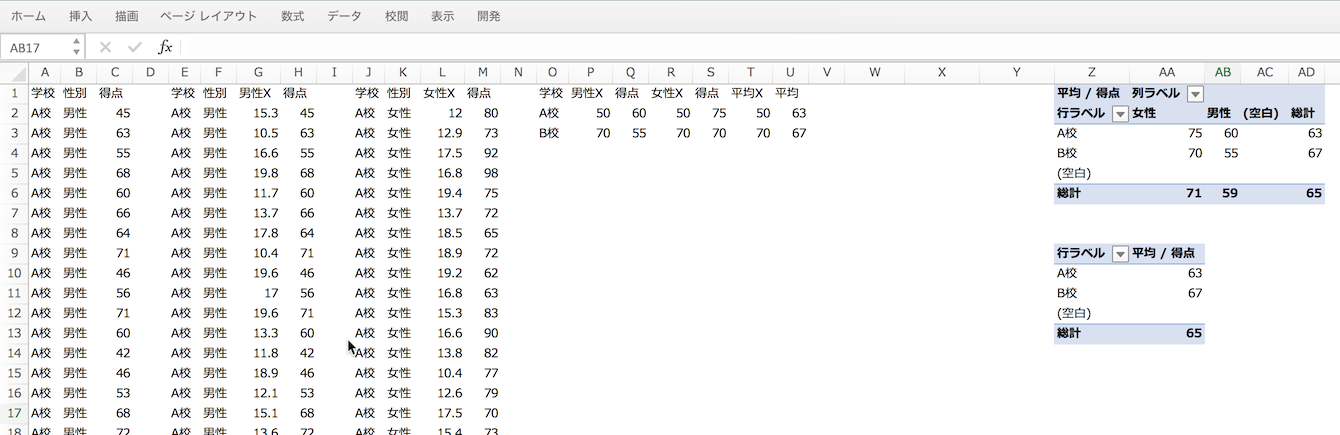
また、そもそも上記のtidyなデータ(いわゆる縦持ちのデータ)ではエクセルでグラフが描けないので系列ごとに加工をしています。A校とB校それぞれのX値の基準をを10と30とし、ジッター(揺らぎ)感を出すためにRANDOM関数を使用して加算しています。下のX軸のタイトルのようなものはテキストオブジェクトを追加で指定しています。系列のデータラベルなどを1つずつ出していくのはカスタマイズできる反面、操作が面倒ですね。下記のような加工をしています。
- 拡大
- 左からオリジナル、系列男性、系列女性、系列男性平均、系列女性平均、系列全体平均となっています。確認のためピボットテーブルも一番右にあります。
さて、出来上がったグラフはこのようになります。
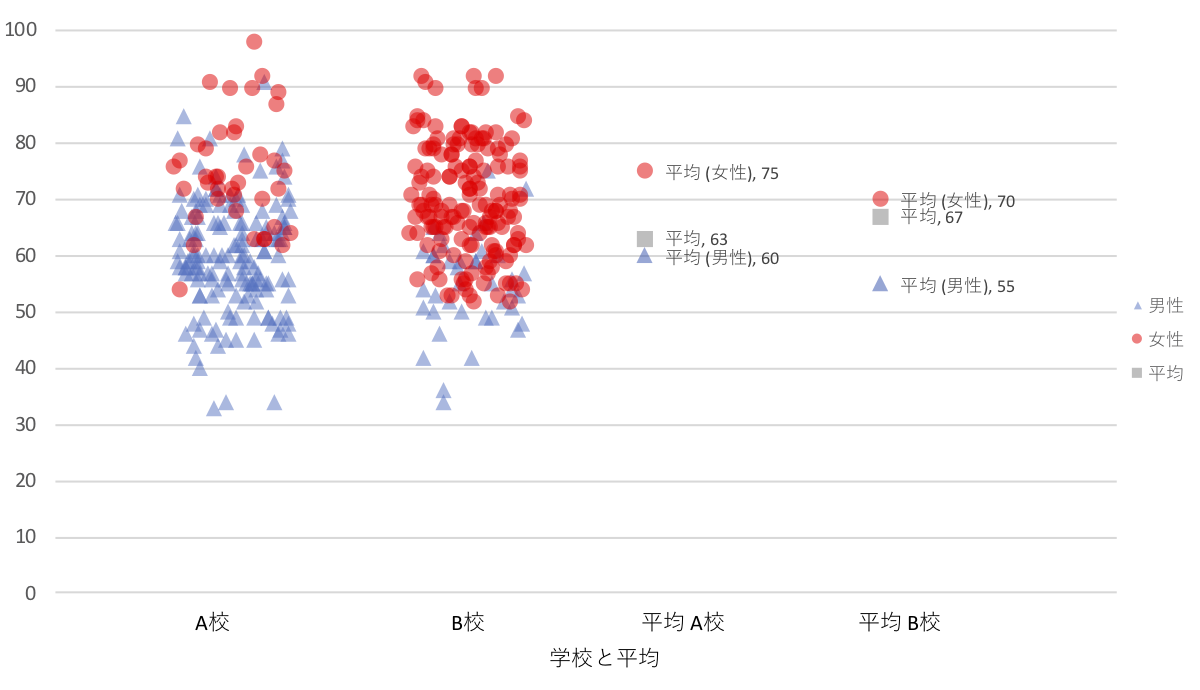
- 拡大
- Microsoft Excelによるシンプソンのパラドックスサンプルグラフ
メリット
- MS製品なので手軽に使える(入手もしやすい)
- 慣れている人が多いので学習コストが低い
- プロパティを設定することで割とカスタマイズがしやすい。
デメリット
- データの加工は手作業で大変
- データを置く場所が自由すぎるため、加工前後でデータの管理がしにくい
- Mac OS用のエクセルはWindows用とコードを統一してから(使い勝手も含めて)不具合が多くないですか?
ということでエクセルのグラフを作成してみました。
次はマイクロソフト社のBIツールであるPower BIを使用してグラフを作成してみました。Power BIもデフォルトで用意されているモジュールに不連続 × 連続に対応しているものがないのでエクセル同様に散布図を駆使して作成しました。A校とB校それぞれのX値の基準をを0と6とし、下記のような列Power BI上で追加しています。
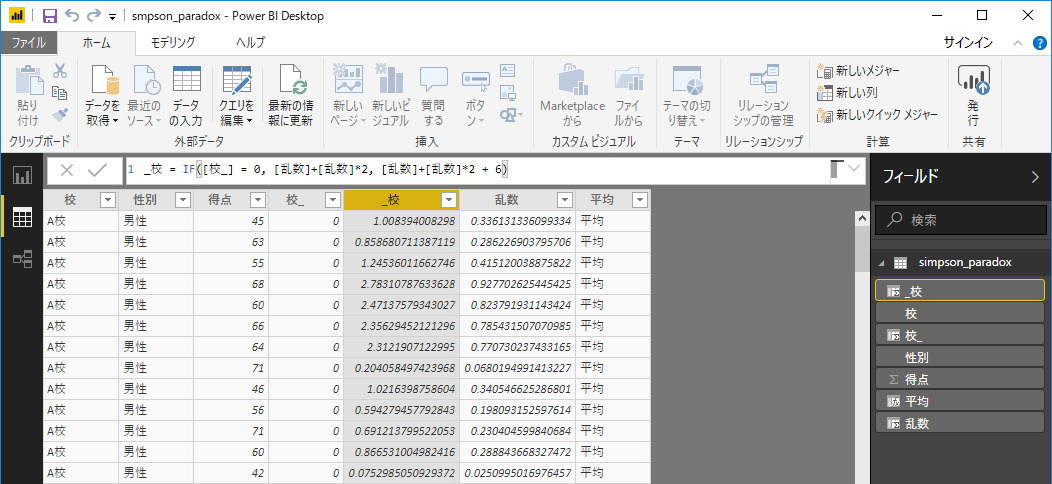
- 拡大
- X軸に入れるため、乱数などで位置を調整した変数「_校」を使用
また、エクセルとは異なり、グラフに対する系列を追加はできないため、ビジュアルをいくつかに分けて作成しています。
出来上がったグラフはこのようになります。
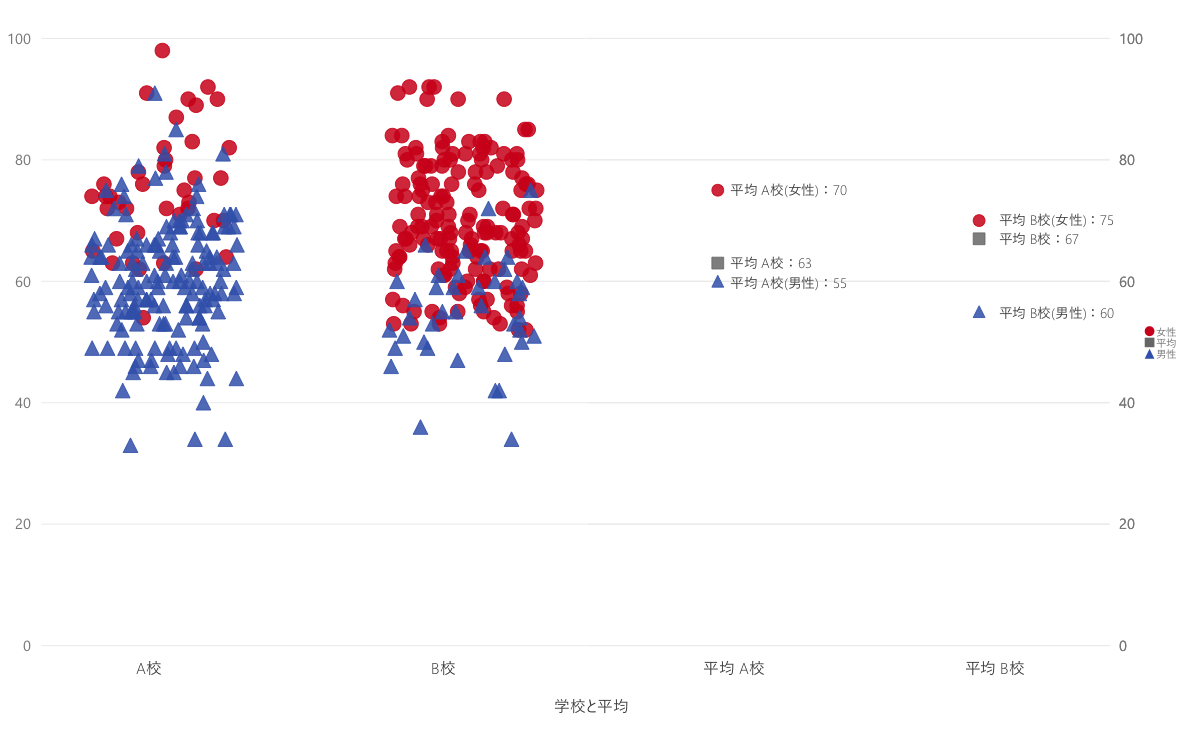
- 拡大
- Microsoft Power BIによるシンプソンのパラドックスサンプルグラフ。左側のグラフ、平均のグラフは性別と全体の2枚を重ねて表示させています(そのため右側の凡例の順序が全体が2番目になってしまっています)。
メリット
- Microsoft製品なので、Excelライクに使用が可能
デメリット
- カスタムビジュアルをインポートしなければならない(ポジティブに捉えればマーケットプレイスから無限の可能性が広がる)のでもう少しデフォルトのセットを増やしてほしい
BIで有名なTableau社のソフトウェアです。普段はTableauを使用して可視化をしているので自分にとっては使いやすいのですが、こちらは不連続 × 連続に対応しているため比較的楽に作成できそうです。ただし同じ値がある場合、集計してしまうので個別に表示させるところで少し躓いてしまいました(JITTER処理の位置が同じ値は同じ場所に配置されてしまっていた)。
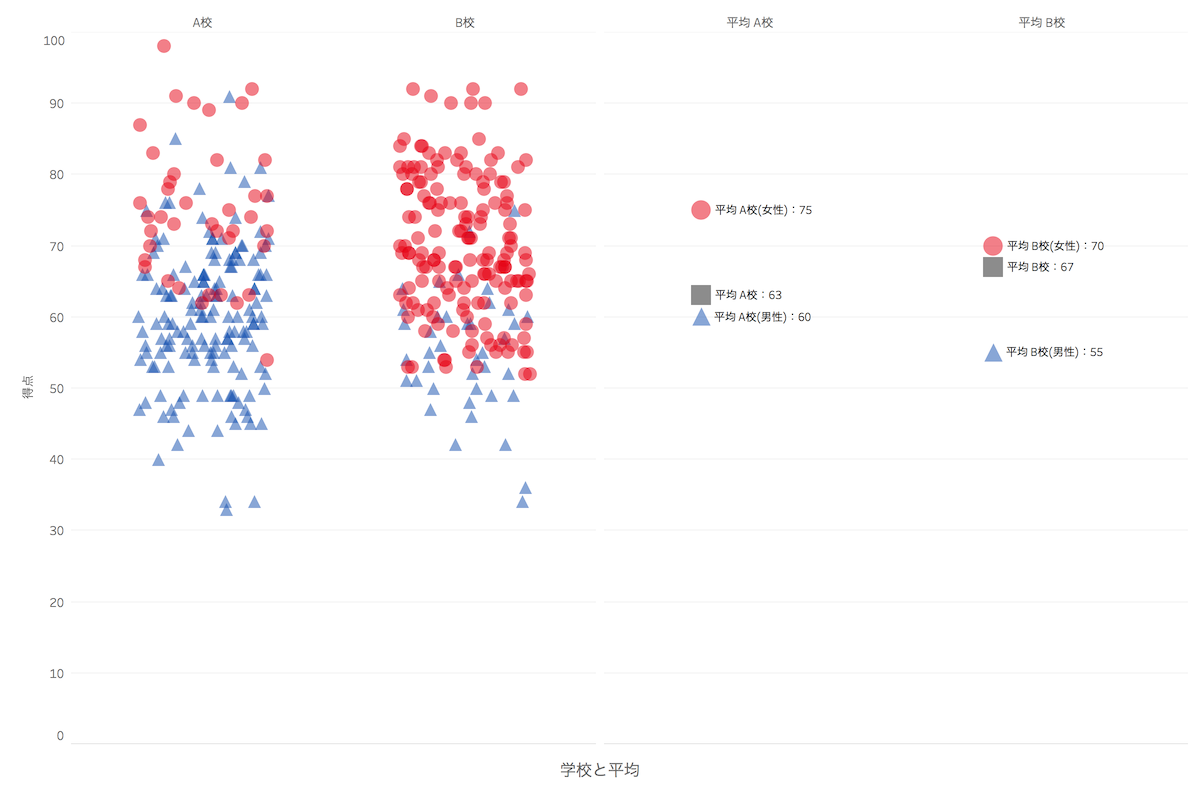
- 拡大
- Tableau Desktopによるシンプソンのパラドックスサンプルグラフ。一番作りやすいグラフでした。
メリット
- 操作性が良い
- 学習コンテンツが充実
デメリット
- データ加工はTableau Prepなど別に必要
- 有償(予算次第ですね!)
とはいえ、まずは無料のTableau Publicを使用して試してみるのも良いのではないでしょうか(一番最後にサンプルは掲載しています)。
*保存したデータは公開されますのでトライアルの際はご注意ください。
Rではggplot2パッケージ(Grammar of Graphicsに基づいた記法)を使用して描画できるのでこちらを使用してグラフを作成してみました。普段はTableauばかりでggplot2パッケージをフル活用できていないため色々と調べることも多く大変でした。
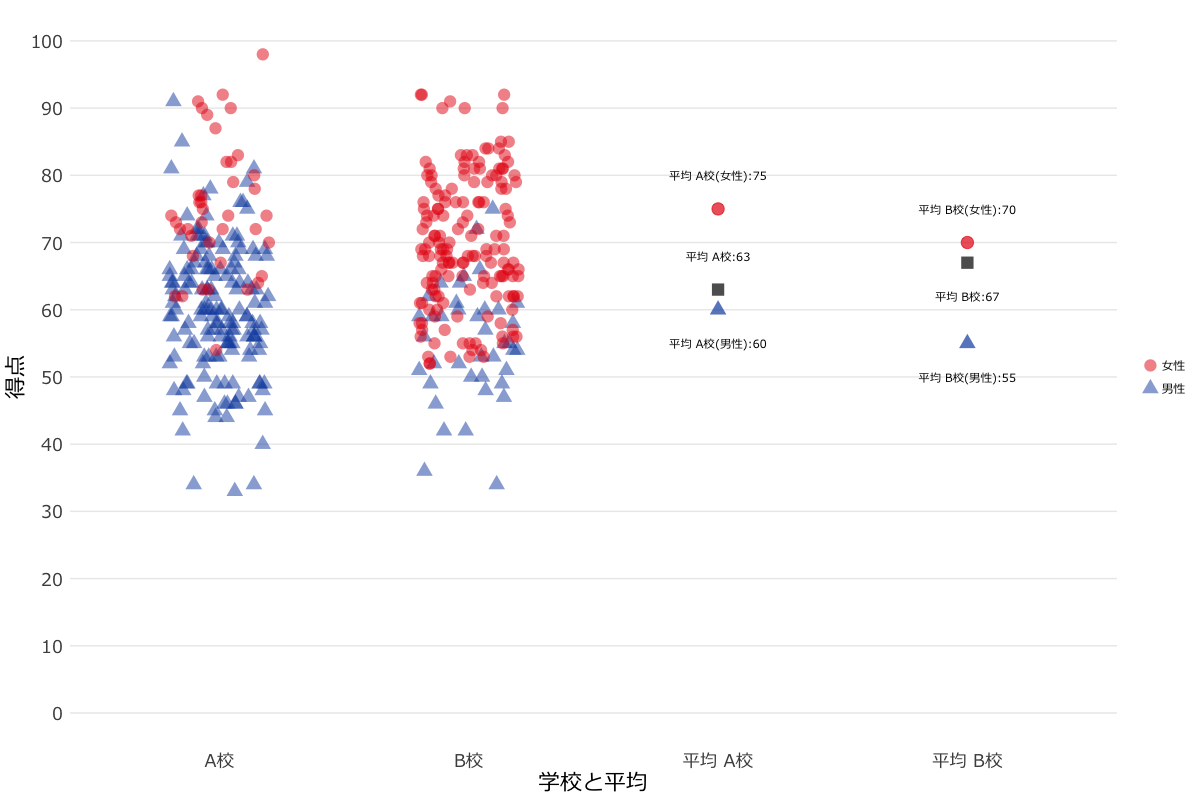
- 拡大
- R & ggplot2パッケージによるシンプソンのパラドックスサンプルグラフ。ggplotの細かい設定はRのコードをご参照ください。
長くなってスミマセン。
| library(ggplot2) |
| # プロパティとして使用する項目の関数 |
| properties <- function() { |
| prop <- NULL |
| prop$add_mean_A_x <- "平均 A校" |
| prop$add_mean_A_y <- round(mean(data[data$学校 == "A校", ]$得点), 0) |
| prop$add_mean_B_x <- "平均 B校" |
| prop$add_mean_B_y <- round(mean(data[data$学校 == "B校", ]$得点), 0) |
| prop$add_mean_a_male_x <- "平均 A校" |
| prop$add_mean_a_male_y <- round(mean(data[data$学校 == "A校" & |
| data$性別 == "男性", ]$得点), 0) |
| prop$add_mean_b_male_x <- "平均 B校" |
| prop$add_mean_b_male_y <- round(mean(data[data$学校 == "B校" & |
| data$性別 == "男性", ]$得点), 0) |
| prop$add_mean_a_female_x <- "平均 A校" |
| prop$add_mean_a_female_y <- round(mean(data[data$学校 == "A校" & |
| data$性別 == "女性", ]$得点), 0) |
| prop$add_mean_b_female_x <- "平均 B校" |
| prop$add_mean_b_female_y <- round(mean(data[data$学校 == "B校" & |
| data$性別 == "女性", ]$得点), 0) |
| return(prop) |
| } |
| # ggplotで描画する関数 |
| my_ggplot <- function(data, prop) { |
| g <- ggplot2::ggplot( |
| data = data, |
| mapping = ggplot2::aes( |
| x = data$学校, |
| y = data$得点)) + # ベースとなるデータの指定 |
| ggplot2::geom_jitter( |
| size = 4, |
| alpha = 0.5, |
| height = 0, |
| width = 0.2, |
| mapping = ggplot2::aes( |
| shape = data$性別, |
| colour = data$性別 |
| ) |
| ) + # 揺らぎを持たせたグラフ描画 |
| ggplot2::scale_color_manual(values = c("#E60012", "#124DAE")) + # 配色指定 |
| ggplot2::annotate( |
| geom = "point", x = prop$add_mean_A_x, y = prop$add_mean_A_y, |
| size = 4, shape = 15, alpha = 0.7) + # A校の平均 |
| ggplot2::annotate( |
| geom = "point", x = prop$add_mean_B_x, y = prop$add_mean_B_y, |
| size = 4, shape = 15, alpha = 0.7) + # B校の平均 |
| ggplot2::annotate( |
| geom = "point", x = prop$add_mean_a_male_x, y = prop$add_mean_a_male_y, |
| size = 4, shape = 17, alpha = 0.7, colour = "#124DAE") + # A校男性の平均 |
| ggplot2::annotate( |
| geom = "point", x = prop$add_mean_b_male_x, y = prop$add_mean_b_male_y, |
| size = 4, shape = 17, alpha = 0.7, colour = "#124DAE") + # B校男性の平均 |
| ggplot2::annotate( |
| geom = "point", x = prop$add_mean_a_female_x, y = prop$add_mean_a_female_y, |
| size = 4, shape = 19, alpha = 0.7, colour = "#E60012") + # A校女性の平均 |
| ggplot2::annotate( |
| geom = "point", x = prop$add_mean_b_female_x, y = prop$add_mean_b_female_y, |
| size = 4, shape = 19, alpha = 0.7, colour = "#E60012") + # B校女性の平均 |
| ggplot2::annotate( |
| geom = "text", family = "Meiryo", size = 3, |
| x = c("平均 A校", "平均 B校"), |
| y = c(prop$add_mean_A_y + 5, prop$add_mean_B_y - 5), |
| label = c(paste0("平均 A校:", prop$add_mean_A_y), |
| paste0("平均 B校:", prop$add_mean_B_y))) + # A校の平均 |
| annotate( |
| geom = "text", family = "Meiryo", size = 3, |
| x = c("平均 A校", "平均 B校"), |
| y = c(prop$add_mean_a_male_y - 5, prop$add_mean_b_male_y - 5), |
| label = c( |
| paste0("平均 A校(男性):", prop$add_mean_a_male_y), |
| paste0("平均 B校(男性):", prop$add_mean_b_male_y))) + # 男性の平均 |
| ggplot2::annotate( |
| geom = "text", family = "Meiryo", size = 3, |
| x = c("平均 A校", "平均 B校"), |
| y = c(prop$add_mean_a_female_y + 5, prop$add_mean_b_female_y + 5), |
| label = c( |
| paste0("平均 A校(女性):", prop$add_mean_a_female_y), |
| paste0("平均 B校(女性):", prop$add_mean_b_female_y))) + # 女性の平均 |
| ggplot2::xlab("学校と平均") + # X軸のラベル |
| ggplot2::ylab("得点") + # Y軸のラベル |
| ggplot2::scale_y_continuous( |
| breaks = seq(0, 100, by = 10), |
| limits = c(0,100), |
| minor_breaks = NULL) + # 縦軸の書式設定 |
| ggplot2::theme_minimal(base_family = "Meiryo") + # テーマとフォント |
| ggplot2::theme(legend.title = element_blank(), |
| axis.title.x = element_text(size = rel(1.5)), |
| axis.title.y = element_text(size = rel(1.5)), |
| axis.text.x = element_text(size = rel(1.5)), |
| axis.text.y = element_text(size = rel(1.5)), |
| panel.grid.major.x = element_blank()) # 凡例と縦軸の削除 |
| return(g) |
| } |
| # 描画 |
| print(my_ggplot(data, properties())) |
メリット
- 高いカスタマイズ性
- 自由(フリー)なソフトウェア
デメリット
- 「完全に無保証」
- 覚えること(プロパティ設定≒コードで追加していく)が多いので敷居が高い?
- マニュアルは英語のものが多い
シンプソンのパラドックスについて概要を確認しました。そしてその例としてサンプルデータを使用して、Excel、Power BI、Tableau、Rで可視化をしてデータのばらつきを確認しました。
いずれも男性や女性といった視点でみるとそれぞれの平均点はA校が高いものの、全体の平均点はB校が高いということになっています。性別で見たときに人数がそれぞれの学校で異なっているため、全体平均で見ると平均点が逆転しているということがグラフから見て取れるのではないでしょうか。
いずれのツールで作成したグラフも似せて作ることはできましたが、ツールの製品仕様やモジュールによっていろいろと工夫をしなければならないことがお判りいただけたかと思いますし、それぞれの特徴についてもなんとなくご理解いただけたのではないでしょうか。[PR]データ分析で普段気づかなかったことを明らかにし、課題解決につなげていきたいですね!
本記事がみなさんのお役に立てれば幸いです。
それでは
Happy Holidays!
- 伊藤徹郎, 2018, データサイエンティスト養成読本 ビジネス活用編, 技術評論社, p.107-108
- 西内啓, 2013, 統計学が最強の学問である, ダイヤモンド社, p.180-184
TableauのグラフはこちらのTableau Publicでも公開しています。




