技術研究所のまつけんです。「鉄道とグラフ理論」の話題は一旦お休みして、先週の月曜日に開催された数学のセミナーについて、本日から2回にわたってレポートさせていただきたいと思います。

先週の月曜日、本社フューチャーセンターにてOpen Innovation Seminar「データサイエンティストに憧れるITエンジニアのためのやり直し数学」を実施しました。2部構成で、第1部は、名桜大学 准教授 當間健明 氏による「深層学習に頼らずとも統計とExcelでここまでできる」ということで、第2部は「超入門! 今日から機械学習の教科書を読めるようになる」と題して、私が担当させていただきました。
第1部では、表計算ソフトウェア+アドオンでモンテカルロ・シミュレーションを行う方法について、実際の例に近い架空の例を用いたデモを交えながら解説していただきました。モンテカルロ・シミュレーションというのは、不確実性をコンピュータでシミュレートするアルゴリズムです。
実際のビジネス現場においても不確定要素が多数あります。そして、ABテストのように実際の現場で実験が行えることもあります。しかし、数十、数百のパターンを現場で試すのは困難です。
そこで、条件を様々に変化させながらシミュレーションを行い、最も効率の良かったプランをビジネス現場に適用する、というアプローチがとられることがあります。
非常に単純な例(注1)を挙げますと、2つのサイコロを投げ、その出た目の合計値を記録していくと二項分布binomial distributionという分布になることが知られています。しかし、本当にそうなのか、実際にサイコロを1,000回も2,000回も投げる実験をして確認するわけにはいきません。そこで、コンピュータで乱数(疑似乱数pseudo random number)を発生させ、それをサイコロに見立てて実験(シミュレーション)することが出来ます。
例えば、MATLAB(注2)を使って「2つのサイコロを10,000回ずつ投げる実験」は以下のような短いコード:
| n = 10000; |
| dice1 = int8(rand(n, 1)* 5 + 1); |
| dice2 = int8(rand(n, 1)* 5 + 1); |
| s = dice1 + dice2; |
| h = histogram(s,11); |
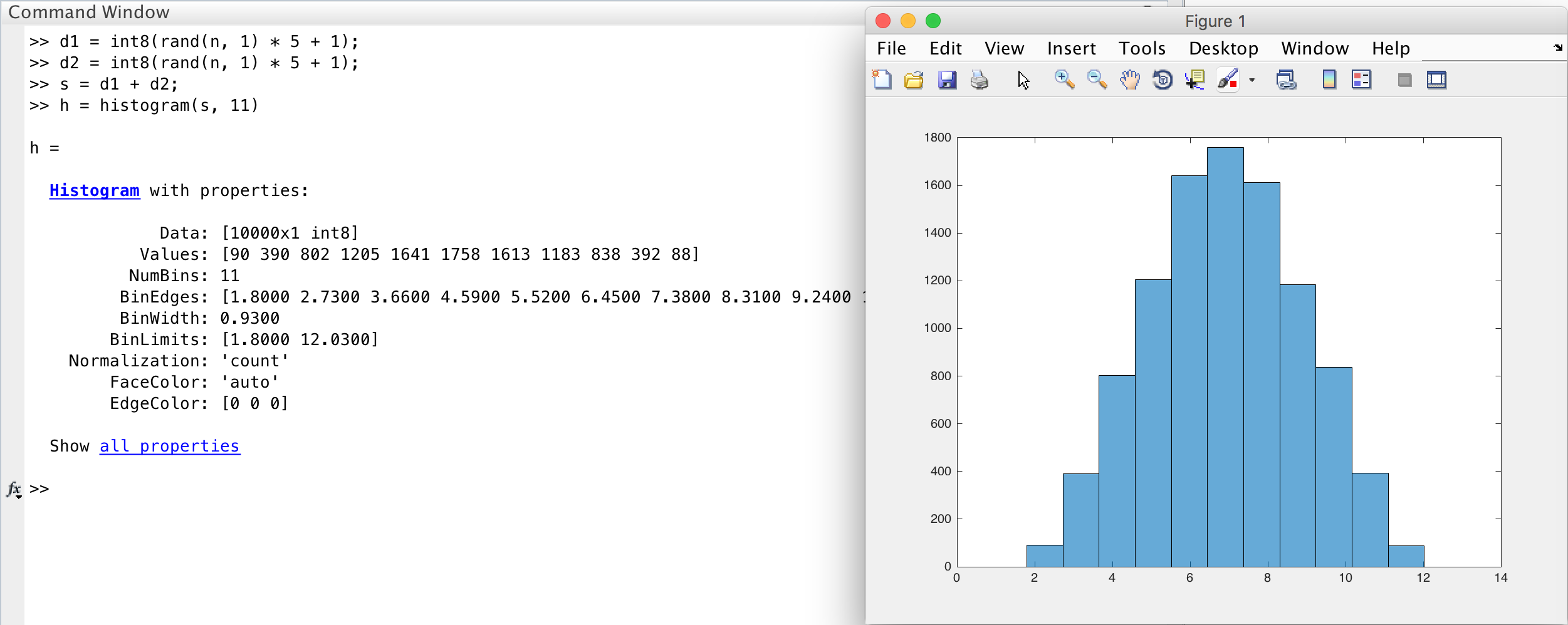
でシミュレートすることが出来ます。最終的にヒストグラムhは以下のような分布になります:
| 合計値 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 回 数 | 90 | 390 | 802 | 1205 | 1641 | 1758 | 1613 | 1183 | 838 | 392 | 88 |
乱数の種random seedを固定せずに乱数を用いているので実行するたびに結果が違いますが、試行回数nが十分に大きければ、毎回ほぼ同じような傾向の結果となります(これを大数の法則といいます)。このhをプロットすると以下のように、中央が高く両端が低い「釣り鐘型の曲線bell curve」となります:
第2部では、機械学習の勉強をしようと思ったときに出てくる初歩的な数式について解説しました。「住宅のスペックからその住宅の価格を推定するAIを作るとしたら?」という例題:
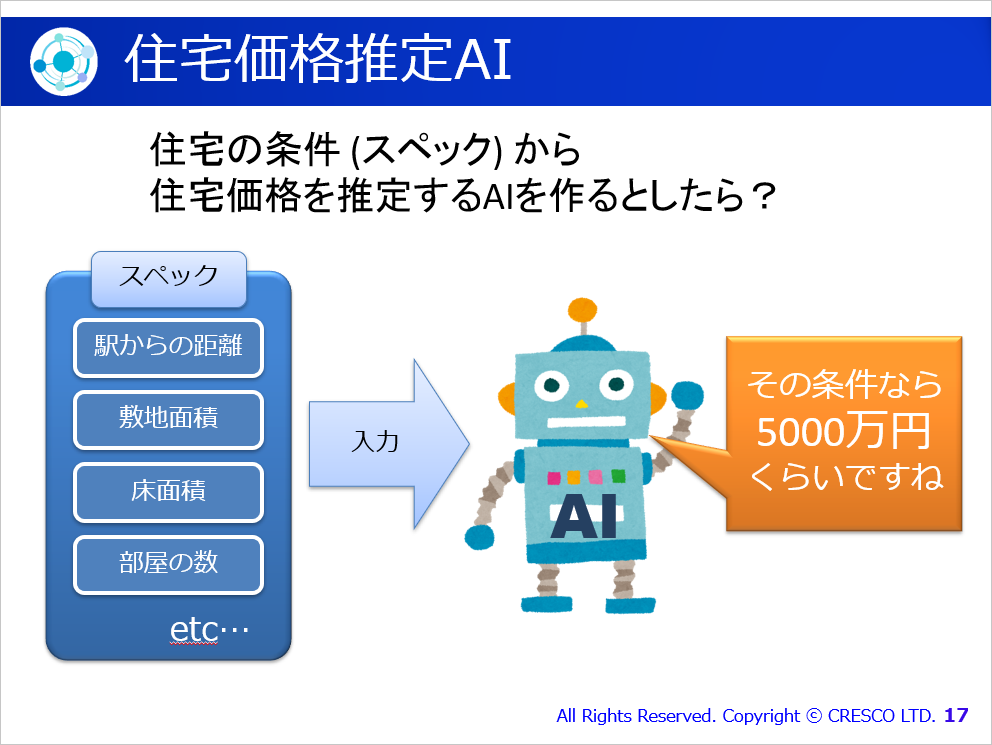
を用いて、ベクトル・行列、最適化、微分(偏微分)について学習する内容としました。長くなってしまったので、第2部の内容については、また次回の記事で紹介したいと思います。
(注1) このような例では、サイコロの目の組み合わせは(1, 1)から(6, 6)の36通りしか無いため、総当たり(全ての場合を試すこと)が可能なので、本来はモンテカルロ・シミュレーションは不要。
(注2) Octaveというフリーウェアでも同様のシミュレーションが可能。




