技術研究所のまつけんです。前回に引き続き、2月25日に開催した数学セミナーのレポートをさせていただきたいと思います。

第2部「超入門! 今日から機械学習の教科書を読めるようになる」では、機械学習の勉強をしようと思ったときに出てくる初歩的な数式について解説しました。「住宅のスペックからその住宅の価格を推定するAIを作るとしたら?」という例題:
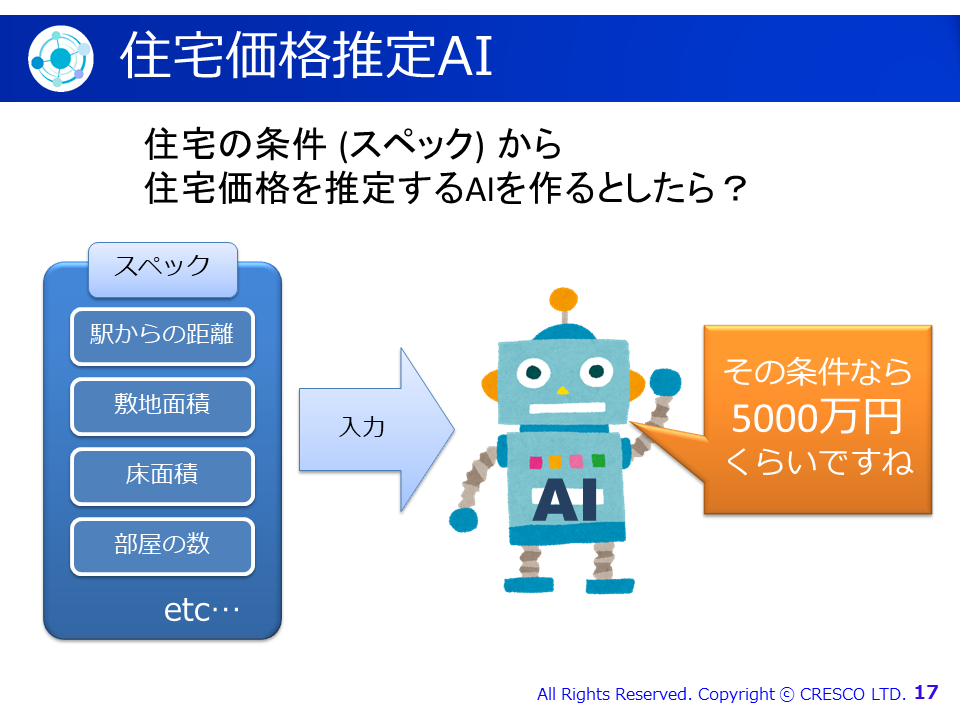
を用いて、ベクトル・行列、最適化、微分(偏微分)について学習する内容でした。
データサイエンティストとは、一言で言うと、

になります。例えば、自車の顧客の動向を分析した結果、「我が社の顧客のうち、40歳代の女性の90%は金曜日の夜に来店している」ということがわかれば、その情報を元にキャンペーンを行うことにより、売り上げや利益を増やすことが出来るかもしれません。
そして、そのためには数学が必要です。今回のセミナーでは「データサイエンスで使う数学」の一部として「機械学習」の基礎知識である、ベクトル・行列、最適化、および、微分(偏微分)を取り上げることとしました:
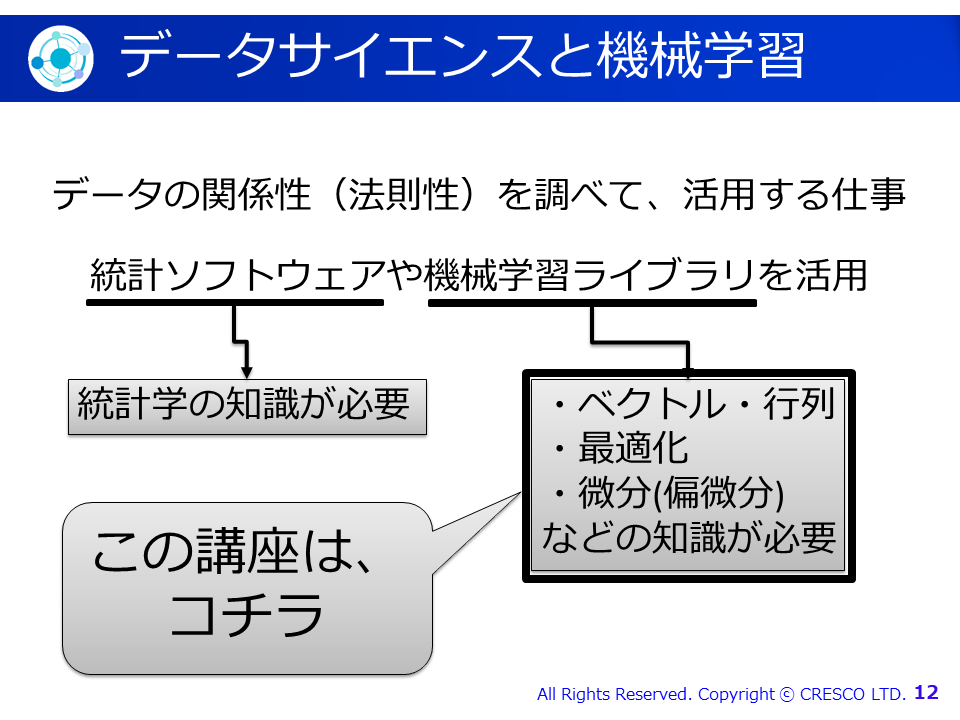
しかし、(当然ですが)数学を勉強しようと思ったら、たくさんの数式に出会います:

数式というのは、なかなか取っつきにくいものなので、たくさんの数式に圧倒されて挫折してしまう方も多いかもしれません。しかし、逆に言えば、これらの数式の意味さえわかってしまえば、セミナータイトルの通り、「機械学習の教科書を読めるように」なるはずです。実際、上記の数式は全て、今回のセミナーで解説しましたので、セミナー後には上記の全てについて、「見たことがある」そして「何となく意味がわかる」状態になって頂いたと思います。
さて、冒頭の例題:
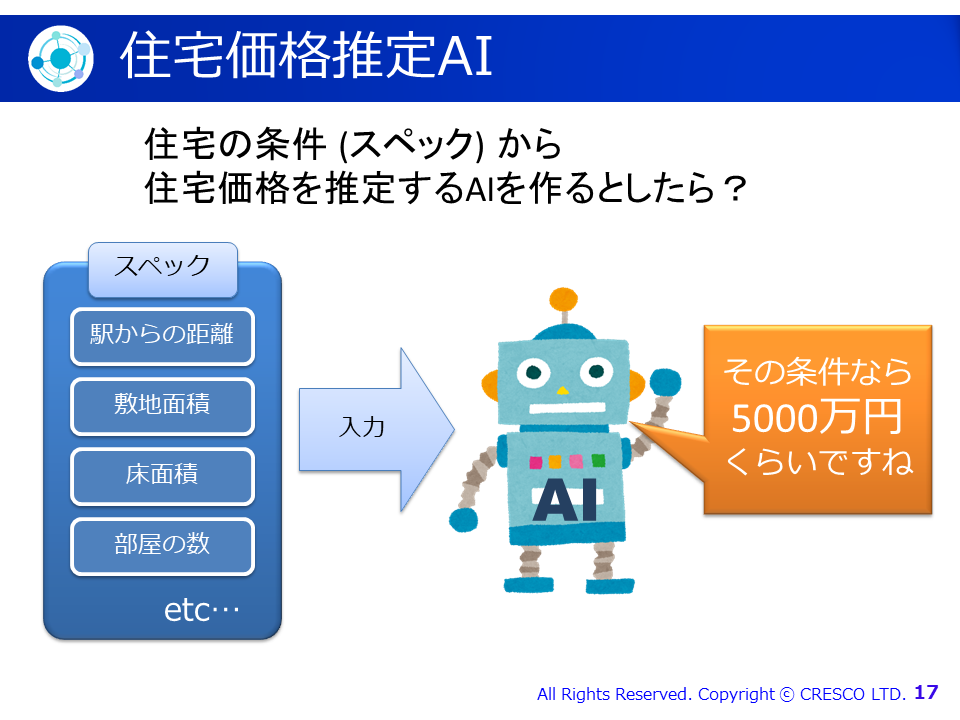
に話を戻しましょう。このAIは、簡易的には以下のような数式で実装できます(注1):
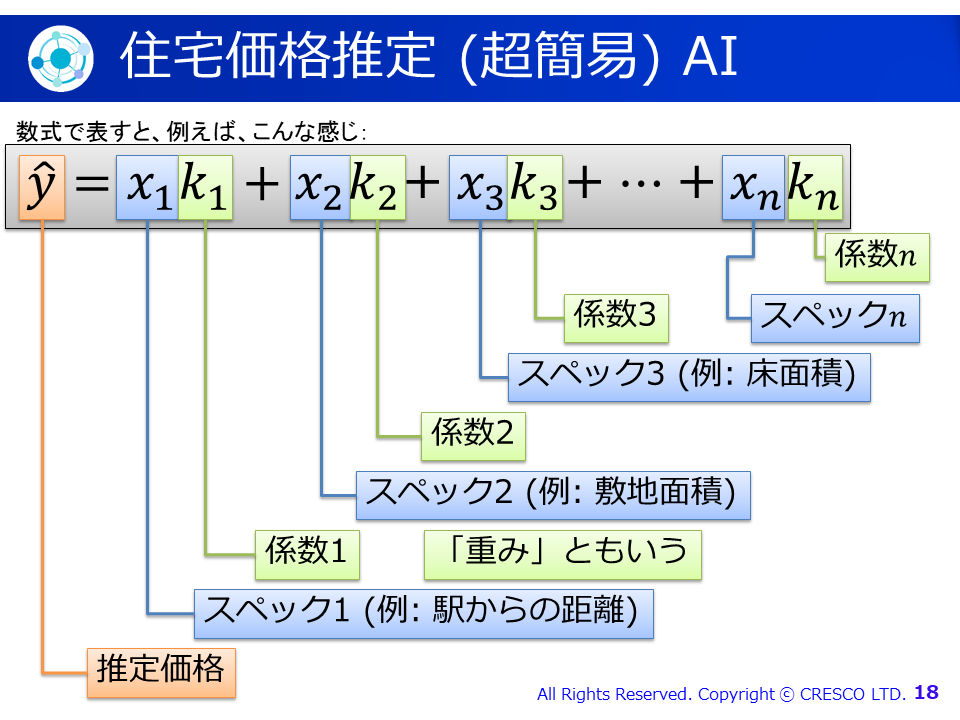
この式を簡潔に表すのに、ベクトル・行列が役に立ちます。また、k1からknまでの係数(重み)を求めるのには、最適化の処理が必要となります。最近は、Pythonでscikit-learnなどのライブラリを使えば、あっという間に係数を求めることが出来ることもありますが、最適化の概念と微分・偏微分を理解していないと、ハイパーパラメタのチューニングなどが正しく行えません。ですから、ベクトル・行列、最適化、および、微分(特に偏微分)は、機械学習を学ぶ上で基本中の基本ということになります。これらに加えて、今回のセミナーでは時間の関係で出来ませんでしたが、固有値eigenvalueと固有ベクトルeigenvector(s)、および、畳み込み積分convolutionを理解すれば、機械学習の内部について理解が深まるかと思います。
今後も、数学セミナーを開催することがあるかもしれませんので、その際は是非、ご参加ください。
(注1) 説明が複雑になるので省略したが、実際には、切片interceptとして定数k_{0}も使った方が好ましい結果が得られることが多い




