はじめに
機械学習には様々な手法があり、その1つに「強化学習」があります。
ですが、ロジックは他の学習手法と比べるとやや難解なものになっています。
本記事は、筆者が強化学習への理解を深めるとともに、これから強化学習を学ぶ人の一助になればという想いで執筆したものとなります。
前半は迷路を用いたシチュエーションを基に強化学習の考え方を、後半はPythonで記載したコードに沿って学習の流れを解説します。
この記事が読者の強化学習に関する理解の手助けになれば幸いです。
なお、本記事で取り扱う題材とサンプルプログラムについては、以下の記事を参考にしております。
DSE総研オンライン編集部. "超簡単な強化学習(Q学習)のPythonコード実装例で一気に理解!【迷路を解く】". 2021-5-18, https://dse-souken.com/2021/05/18/ai-17/
(参照 2024-3-29)
本記事では強化学習の数式についての詳しい解説は省き、学習のプロセスに焦点を当てて解説しています。
引用元では数式も詳しく解説されておりますので、本記事で興味を持った方はぜひ見てみてください!
目次
- 強化学習とは(強化学習で使う用語は2章で説明)
- 学習の概要
- 強化学習のプロセス
- サンプルプログラムとQ値の可視化
- まとめ
1.強化学習とは(強化学習で使う用語は2章で説明)
強化学習とは、AIの学習手法の一つであり、特定の目標を達成するために最適な行動を学習する手法です。試行錯誤を繰り返し、その過程で得られる報酬をもとに最良の行動を見つけます。
同じAIの学習手法の一つである教師あり学習は、事前にラベル付けされた学習データ(答えのついたデータ)を用いて、出力結果が望ましいものになるようにモデルを学習させます。例えば、犬や猫の画像とそのラベルから、新たな画像が犬なのか猫なのかを予測します。
つまり、教師あり学習はあらかじめ答えが分かっている問題(例:この写真は犬 or 猫?)を解くのに特化し、強化学習は報酬やマイナスの報酬を通じて最善の行動を自己学習します。どちらもAIを使った学習方法ではありますが、このように大きく異なる特性をもっています。
本ブログでは強化学習の一つである「Q学習」について、強化学習の題材としてよく取り上げられる「迷路ゲーム」で解説します。
迷路ゲームは直感的に分かりやすいため、強化学習の初学者でも理解しやすい内容だと思います!
2. 学習の概要
本記事では後述するプロセスを含め、「迷路」と「迷路を移動するロボット」を例として解説します。 この「迷路を移動するロボット」は エージェント と呼ばれます。
「迷路はマス目状に作成され、スタートとゴールがそれぞれ1つ存在し、それをエージェントが解いていく」といったイメージです。
そして、この迷路での最終目標は「迷路に挑戦し、ゴールまでの最短距離を見つけること」になります。
しかし、このエージェントは迷路の地図を持っているわけではありません。できることはあくまで移動のみ、最初はゴールの位置すら不明です。 闇雲に進んでいっては何度も同じ壁にぶつかってしまう可能性があります。 (一応は迷路なので、壁伝いで進めば必ずゴールへ着きます。が、それが最短距離であることはごく稀です)
そこで、このエージェントが移動するたびに採点を行い、エージェントはその採点内容を知ることができるようにします。 (「ゴールは10000点」「1マス移動すると1点」「移動不可なマスや壁で隔たれた方向への移動は0点」といったように)
エージェントの移動は行動、行動に対する採点は報酬と呼び、 エージェントは最短距離で大きな報酬をもらえるように行動を選択します。
また、行動を選択するにあたって「もし今の場所から前に移動するとより大きな報酬がもらえる」「もし右に移動すると袋小路だ(報酬がもらえない)」といったように、移動先の報酬をあらかじめ考えながら行動を最適化していくといった方法をとります。
この「今エージェントがいるマス目(状態)からの行動はどれくらい報酬が期待できるか」を表す指標を行動価値と呼びます。 (価値にはもう一つ、状態価値というものがありますが今回は説明を省略します)
しかし、一回目の挑戦で最短ルートを見つけ出すというのは天文学的な確率。上記の報酬獲得ルールだとマスに移動さえすれば1点もらえます。つまり、今いる場所から進んでも戻っても価値は等しく1点。場合によっては同じ場所を行ったり来たりしてしまうこともあります。
移動を繰り返すことで、時間はかかれどゴールにはたどり着けるでしょう。しかしこれでは最短距離とは言い難いです。
そこで、「2回目では前の挑戦で得た行動価値を参考にして、次の行動価値を更新」します。
以下で説明するQ学習では行動価値をQ値、迷路へ挑戦することをエピソードと呼称し、エピソードを繰り返すことで最短距離を導き出しています。
3. 強化学習のプロセス
Q学習のプロセスを、迷路の例で説明します。
3.1. 報酬を決める:
まず、エージェントが移動した際の採点結果である報酬を定義する必要があります。
当然、ゴールした場合の報酬はそれ以外の報酬より高くするべきですので、今回は以下のように設定してみます。
- ゴールにたどり着ける場合は10000(今回の例だと5➝8のみ)
- 移動が不可能な場合は0(例えば壁のある2➝5や移動のない0➝0の場合)
- 移動が可能な場合は1(上記以外)
なお、今回は報酬が0(移動が不可能な場合)の行動は選択できないようにしています。
この報酬は9×9の行列を用いて表すことができそうです。
これをここでは報酬行列Rと呼ぶこととします。(専門用語ではないです。)
例えば、状態0から1に移動する行動をとる場合の報酬は、R(0, 1)=1と表すことができます。
reward = np.array( |
[ |
[0, 1, 0, 1, 0, 0, 0, 0, 0], # 0から1,3に移動できるので、そこに1 |
[1, 0, 1, 0, 0, 0, 0, 0, 0], # 1から0,2に移動できるので、そこに1 |
[0, 1, 0, 0, 0, 1, 0, 0, 0], |
[1, 0, 0, 0, 1, 0, 1, 0, 0], |
[0, 0, 0, 1, 0, 1, 0, 1, 0], |
[0, 0, 1, 0, 1, 0, 0, 0, 0], |
[0, 0, 0, 1, 0, 0, 0, 0, 0], |
[0, 0, 0, 0, 1, 0, 0, 0, 10000], # 8がゴールのため7→8の報酬を大きく |
[0, 0, 0, 0, 0, 0, 0, 1, 0], |
] |
) |
3.2. 初期化:
まずは全ての状態と行動の組み合わせに対するQ値を初期化します。
今回の例では、エージェントの状態と行動の組み合わせは、報酬行列と同様に9×9の行列で表すことができます。
例えば、状態0から1に移動する行動をとる場合のQ値は、Q(0, 1)と表せます。
今回はこの行列Qの要素を全て0として初期化します。(ランダムな小さい値を用いて初期化することもあります。)
Q = np.array(np.zeros(reward.shape)) |
3.3. エージェントの移動と報酬の観測:
エージェントはある状態において選択可能な行動を一つ行い、その結果得られる報酬を観測します。(ここで、ある状態のことをs、選択した行動をa、得られる報酬をrとします。)
例えば、エージェントが初期状態で0のマスにいるとき(s=0)、選択可能な行動aは1または3への移動のどちらかです。
行動の選び方にはいくつかの方法がありますが、今回はランダムに選択することとします。(一般的にはε-greedy法が用いられることが多いですが、今回は省略します。)
next_state = np.random.choice(next_actions) |
ランダムに選ばれた行動aに対して報酬行列に基づいて報酬rを計算します。
たとえば状態0から1へ移動した場合、報酬行列の(0,1)から報酬r=1を得ることになります。
reward[current_state, next_state] |
3.4. Q値の更新:
得られた報酬rをもとに、先ほどの状態sと行動aに対するQ値を更新します。更新式は以下のようになります。(この更新式は偉い人が考えた式です)
Q(s, a) ← (1- α)Q(s, a) + α * [r + γ * max(Q(s', a'))]
偉い人の考えを読み解くと、以下のようになります。
・Q(s, a):状態sで行動aを選んだときのQ値
・max(Q(s', a')):行動aによって移動した後の状態s'において、選択できる全ての行動a'に対する最大のQ値
・α:学習率(どれくらい新しい情報を反映するかを決定するハイパーパラメータ)
・γ:割引率(将来の報酬をどのくらい重視するかを決定するハイパーパラメータ)
よって更新式は、ざっくり以下のように言い換えられます。
更新後のQ値=更新前のQ値+(今回の報酬+移動後の状態で選択できる行動の中で最大のQ値)
Q値の更新式中のγ * max(Q(s', a'))項は、次の状態で取りうるすべての行動の中で最もQ値が大きいものを取り出し、そのQ値にγを掛けたものになります。
つまり、現在の報酬だけでなく、将来得られるであろう報酬も(γ分だけ)考慮してQ値が更新されます。
これにより、長期的に最も報酬が大きくなるようにQ値が更新されていきます。
なお、学習率αと割引率γの詳細については今回は割愛します。
サンプルプログラムでは以下のように計算しています。
Q[current_state, next_state] = (1 - alpha) * Q[ |
current_state, next_state |
] + alpha * ( |
reward[current_state, next_state] |
+ gamma * Q[next_state, np.argmax(Q[next_state,])] |
) |
3.5. 学習の繰り返し:
上記ステップ3とステップ4を繰り返し行います。
ただし、初期状態0からスタートし、ゴールの8に到達するまでの1エピソードを連続して行います。(つまり、ステップ3で0から1に移動した場合、ステップ4の更新をした後、エージェントが1にいる状態で次のステップ3を行います。これを、1エピソード終了するまで行います。)
そして、このエピソードを何回か繰り返し行うことで、Q値が最適な値になっていきます。
4. サンプルプログラムとQ値の可視化
以上のプロセスを基に作成されたプログラムがこちらです。
(引用元で公開されているプログラムにヒートマップ関数を追加しています)
Google Colab上で動作するので、皆さんも動かしてみてください。
import numpy as np |
import matplotlib.pyplot as plt |
import matplotlib as mpl |
|
gamma = 0.9 # 割引率 |
alpha = 0.1 # 学習率 |
|
# 報酬の設定 |
# 移動が可能な場合は1、移動が不可能な場合は0、ゴールとなる8の報酬を10000とする |
reward = np.array( |
[ |
[0, 1, 0, 1, 0, 0, 0, 0, 0], # 0から1,3に移動できるので、そこに1 |
[1, 0, 1, 0, 0, 0, 0, 0, 0], # 1から0,2に移動できるので、そこに1 |
[0, 1, 0, 0, 0, 1, 0, 0, 0], |
[1, 0, 0, 0, 1, 0, 1, 0, 0], |
[0, 0, 0, 1, 0, 1, 0, 1, 0], |
[0, 0, 1, 0, 1, 0, 0, 0, 0], |
[0, 0, 0, 1, 0, 0, 0, 0, 0], |
[0, 0, 0, 0, 1, 0, 0, 0, 10000], # 8をゴールより7→8の報酬を大きくする |
[0, 0, 0, 0, 0, 0, 0, 1, 0], |
] |
) |
# Q値(行動価値)の初期値を設定。今回は0を初期値とする。 |
Q = np.array(np.zeros(reward.shape)) |
# Q学習を実装し、各位置における行動価値を算出 |
# 以下の学習を実行すると、行動価値Qを求められる。Qの各行が位置に対応し、たとえば0行1列目の値は0から1に移動する行動の価値となる。 |
|
|
# Q値のヒートマップ作成用関数 |
def plot_heat_map(): |
heat_vec = np.array(np.zeros(len(reward))) |
for k in range(0, len(reward) - 1): |
for l in range(k + 1, len(reward)): |
if reward[k, l] >= 1: |
heat_vec[l] += Q[k, l] |
if k == 4 and l == 5: |
heat_vec[k] += Q[l, k] |
|
heat_vec[4] /= 2 |
heat_vec[5] /= 2 |
heat_map = heat_vec.reshape([int(len(reward) ** 0.5), -1]) |
fig, ax = plt.subplots() |
im = ax.imshow(heat_map) |
for k in range(int(len(reward) ** 0.5)): |
for l in range(int(len(reward) ** 0.5)): |
text = ax.text( |
l, k, round(heat_map[k, l], 2), ha="center", va="center", color="w" |
) |
plt.show() |
|
|
for i in range(200): # 200エピソードを繰り返し学習を行う |
if i % 5 == 0: # 5エピソードごとにヒートマップを表示 |
plot_heat_map() |
|
current_state = 0 # 初期位置は0 |
while current_state != 8: # 1エピソードが終了するまでのループ |
next_actions = [] # 次の行動の候補を格納するリスト |
for j in range(9): |
if reward[current_state, j] >= 1: |
next_actions.append(j) # current_stateの状態で移動できる場所を格納 |
next_state = np.random.choice(next_actions) # 行動可能選択肢からランダムに選択 |
|
# Q値の更新式 |
Q[current_state, next_state] = (1 - alpha) * Q[ |
current_state, next_state |
] + alpha * ( |
reward[current_state, next_state] |
+ gamma * Q[next_state, np.argmax(Q[next_state,])] |
) |
current_state = next_state # 次の状態をセット |
|
|
# 最短ルート表示関数。Q値が最も高い行動を順番に追加していく |
def shortest_path(start): |
path = [start] # pathに経路を追加していく |
current_pos = start # current_posは現在位置 |
next_pos = -1 # next_pos(次の位置)をてきとうな値で初期化 |
while next_pos != 8: # next_posがゴール(8)になるまで繰り返し行動を選択 |
next_pos = np.argmax(Q[current_pos,]) # 各位置の行動価値が最も高い行動を選択 |
path.append(next_pos) # 経路をpathに追加 |
current_pos = next_pos # 行動後が次のcurrent_posとなる |
return path |
|
|
print(shortest_path(0)) # スタートを0として最短経路を表示 |
なお、上記のプログラムではQ値の可視化も行っています。
結果は以下のようになります。
数値が高いマスほど、そのマスに移動する行動の価値(Q値)が高いことを意味します。
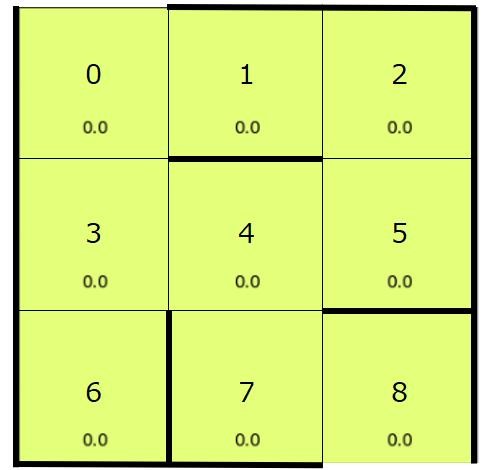
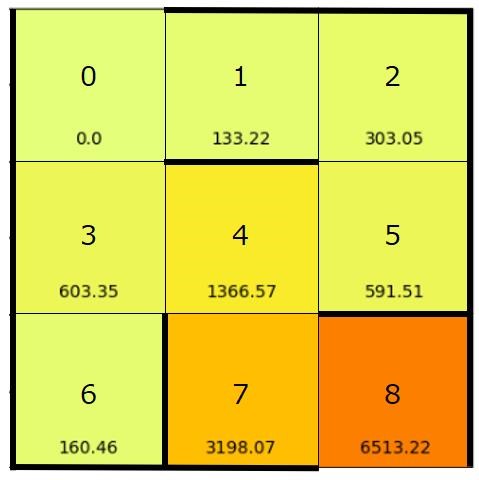
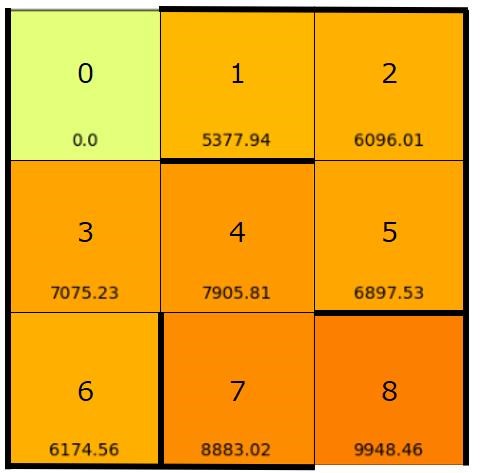
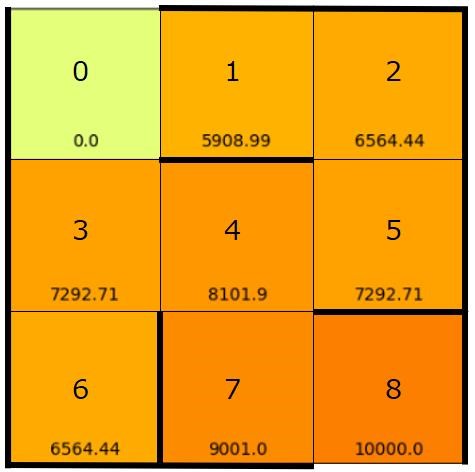
5.まとめ
初めてQ学習を学習するまでは、理解に曖昧な部分があり、どこか良く分からないままやっていたことがありました。しかし、引用元の記事を通じて、Q学習の理論と背景についてより深い理解ができました。
Q学習を学ぶことで、理解のしやすい要素と非常に直接的な実用性のあるアルゴリズムに触れることができました。
今後はQ学習だけでなく、他の強化学習のアルゴリズムや、その理論的背景についても学ぶことで、より深い理解を深めていきたいと考えています。
(引用元)DSE総研オンライン編集部. "超簡単な強化学習(Q学習)のPythonコード実装例で一気に理解!【迷路を解く】". 2021-5-18, https://dse-souken.com/2021/05/18/ai-17/
(参照 2024-3-29)
※ソースコードの引用については、データサイエンス教育総合研究所(DSE総研)様の許諾を得ております(2024-6-7)。 DSE総研 https://dse-souken.com/




