目次
- はじめに
- 従業員の割り当てに関する問題
- 問題の定式化
- プログラム全体
- 従業員のスケジュール設定に関する問題
- 問題の定式化
- プログラム全体
- ⾞両ルートに関する問題
- 問題の定式化
- プログラム全体
はじめに
こんにちは、AIテクノロジーセンターの大川です。
この記事では、Or-Tools公式サイトの「ガイド」に当たる部分を、出来るだけ専⾨⽤語や数式を使⽤せず解説していきたいと思います。
公式ガイド: https://developers.google.com/optimization/introduction?hl=ja
公式サイトによると、Or-Toolsは以下のように書かれています。
「OR-Tools は組み合わせ最適化向けのオープンソース ソフトウェアです。これは、⾮常に広範な可能性のあるソリューションの中から問題に対する最適なソリューションを⾒つけるものです。」
とありますが、具体的に何をするツールなの?というと、例えば以下のような問題を解いてくれるツールとなります。
- 従業員の作業割り当て: 従業員に作業を割り当てるとき、最も作業コストが最⼩になるのはどんな組合せか?
- 従業員のシフト割り当て: 従業員にシフトを割り当てるとき、どんなスケジューリングをするのが最適か?
- ⾞両ルート: ある⾞両が決められた⽬的地を訪問するとき、巡回コストが最⼩になる経路は?
以上に挙げたような問題は、⼿作業で割り当てしている企業様も多いかと思います。こういった割り当て作業を⾃動で⾏ってくれるツールとなります。 具体的には、「数理最適化」という考え⽅で問題解決を⾏います。数理最適化は数学の要素が強いものですが、簡単に書くと
- ⽬的は何か?
例: コストを最⼩にしたい、報酬を最⼤にしたい、等。 - ⽬的を達成するに当たる制約は?
例: このルートは通らないでほしい、この従業員はこの作業には割り当てないでほしい、等。
以上の2つを事前に決めて数式(プログラム)を組み⽴て、それらを満たす解法(ソリューション)を⾒つける⼿法となります。 それでは、問題とその解決 (最適なソリューションの発⾒) までの流れを解説していきます。
従業員の割り当てに関する問題
公式サイト: 割り当ての問題の解決
問題の定式化
問題: ある⼀連の作業について、複数の従業員をそれぞれのタスクに割り当てたい。 それぞれの作業⼯程において、従業員に得意不得意がある。 得意な作業は作業コストが低く、不得意な作業は作業コストが⾼い。
.png)
このとき⼀連の作業コスト全体を最⼩にするには、どの従業員をどの作業に割り当てればよいか︖
pythonのプログラムで、上記の表を以下のリストにします。
| costs = [[90, 80, 75, 70], |
| [75, 85, 55, 65], |
| [125, 95, 125, 95], |
| [45, 110, 95, 115]] |
上記の問題を「⽬的」「制約」に定式化します。
- ⽬的: ⼀連の作業コストを最⼩にする
- 制約: 全ての従業員は、必ず1つの作業が割り当てられる。
ソルバーへの、制約の設定は以下のようにします。
| # 制約: 従業員は1つの作業が割り当てられる. |
| for i in range(data.num_workers): |
| solver.Add(solver.Sum([x[i, j] for j in range(data.num_tasks)]) == 1) |
ソルバーへの、⽬的の設定は以下のようにします。
| # ⽬的: 作業コストを最⼩にする |
| objective_terms = [] |
| for i in range(data.num_workers): for j in range(data.num_tasks): |
| objective_terms.append(costs[i][j] * x[i, j]) solver.Minimize(solver.Sum(objective_terms)) # Minimize -> 最⼩ |
プログラムを実⾏した結果、以下のように出⼒されます。
| 「1さん」は「作業4」に割り当てられました。作業コストは70です。 |
| 「2さん」は「作業3」に割り当てられました。作業コストは55です。 |
| 「3さん」は「作業2」に割り当てられました。作業コストは95です。 |
| 「4さん」は「作業1」に割り当てられました。作業コストは45です。 |
| 合計の作業コストは265.0です。 |
プログラム全体
※次以降の例もですが、公式ガイドを基準に型アノテーションや⽇本語コメントの追加を⾏っています。
| from dataclasses import field |
| from pydantic import StrictInt |
| from pydantic.dataclasses import dataclass |
| from typing import List |
| from ortools.linear_solver import pywraplp |
| from ortools.linear_solver.pywraplp import Solver, Objective |
| @dataclass |
| class Data: |
| """問題に関するデータ定義 |
| Attributes: |
| costs (List[List[int]]): 各従業員が⾏う作業コスト |
| num_workers: 作業員の⼈数 |
| num_tasks: ⼀連の作業⼯程数 |
| """ |
| costs: List[List[int]] = field(default_factory=list) |
| num_workers: StrictInt = field(init=False) |
| num_tasks: StrictInt = field(init=False) |
| def __post_init__(self): |
| self.num_workers = len(self.costs) |
| self.num_tasks = len(self.costs[0]) |
| def main(): |
| # 各従業員が⾏う作業コストを定義 |
| costs = [[90, 80, 75, 70], |
| [75, 85, 55, 65], |
| [125, 95, 125, 95], |
| [45, 110, 95, 115], |
| ] |
| data = Data(costs=costs) |
| # ソルバーのインスタンス作成 |
| solver: Solver = pywraplp.Solver.CreateSolver("SCIP") |
| if not solver: |
| return |
| # 変数を作成 x[i, j]: iは従業員, jは作業. xは0か1のバイナリ整数. |
| # x == 1 なら, iはjに割り当てられたことを表している. |
| x = {} |
| for i in range(data.num_workers): |
| for j in range(data.num_tasks): |
| x[i, j] = solver.IntVar(lb=0, ub=1, name=f"x({i}, {j})") |
| # 制約: 従業員は1つの作業が割り当てられる. |
| for i in range(data.num_workers): |
| solver.Add(solver.Sum([x[i, j] for j in range(data.num_tasks)]) == 1) |
| # ⽬的: 作業コストを最⼩にする |
| objective_terms = [] |
| for i in range(data.num_workers): |
| for j in range(data.num_tasks): |
| objective_terms.append(costs[i][j] * x[i, j]) solver.Minimize(solver.Sum(objective_terms)) # Minimize -> 最⼩ |
| # ソルバーの実⾏ |
| status = solver.Solve() |
| # ソリューションのコンソール出⼒ |
| if status in [Solver.OPTIMAL, Solver.FEASIBLE]: |
| assignment: Objective = solver.Objective() |
| for i in range(data.num_workers): |
| for j in range(data.num_tasks): |
| if x[i, j].solution_value() > 0.5: |
| print(f"「{i+1}さん」は「作業{j+1}」に割り当てられました。作業コストは{costs[i][j]}です。") |
| print(f" 合計の作業コストは{assignment.Value()}です。") else: |
| print("ソリューションが⾒つかりませんでした。") |
| if __name__ == "__main__": |
| main() |
従業員のスケジュール設定に関する問題
公式サイト: 従業員のスケジュール設定
問題の定式化
問題: ある病院で、次の条件で5⼈の看護師を7⽇間にわたるスケジュールを作成したい。
- 毎⽇、3つの8時間シフトに分けられる。
- 毎⽇、各シフトは1⼈の看護師を割り当て、1⽇に複数のシフトに割り当ててはならない。
- シフトは均等に割り当てる。
- 各看護師を、下図のように出来るだけ指定した⽇のシフトに割り当てたい。
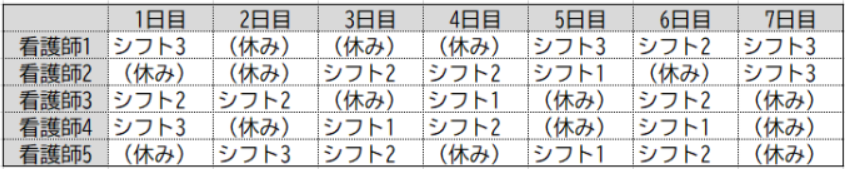
上記のシフトリクエストを、ソルバーに読ませるための配列を作成します。 希望シフトを1、そうでない場合0に設定しています。
| # [看護師1:[1⽇⽬:[シフト1, シフト2, シフト3], ..., 7⽇⽬:[シフト1, シフト2, シフト3], ...], |
| # ..., |
| # 看護師5:[1⽇⽬:[シフト1, シフト2, シフト3], ..., 7⽇⽬:[シフト1, シフト2, シフト3], ...]] |
| shift_requests = [ |
| [[0, 0, 1], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 1]], |
| [[0, 0, 0], [0, 0, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [0, 0, 0], [0, 0, 1]], |
| [[0, 1, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0], [0, 1, 0], [0, 0, 0]], |
| [[0, 0, 1], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0]], |
| [[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0]], |
| ] |
こうして⾒ると、例えば1⽇⽬のリクエストではシフト1が無くシフト3は2⼈割り当てられています。 公式ガイドのデータなので、シフト1は誰でも可能でシフト3は看護師1か4に割り当ててほしい、ということかもしれません。
次に問題を「⽬的」「制約」に定式化します。
- ⽬的: 各看護師を、出来るだけ指定した⽇のシフトに割り当てたい。
- 制約1: 毎⽇、3つの8時間シフトに分ける。
- 制約2: 毎⽇、各シフトは1⼈の看護師を割り当て、1⽇に複数のシフトに割り当ててはならない。
- 制約3: シフトは、出来るだけ均等に割り当てたい。
目的: 各看護師を、出来るだけ指定した⽇のシフトに割り当てたい。
shifts[(n, d, s)] が「n: 看護師, d: ⽇, s: シフト」を表す変数で、シフトが割り当てられたら1、そうでなければ0が代⼊されます。 出来るだけシフトリクエスト通りに割り当ててほしいので、⽬的は最⼤化、つまり Maximize() を使⽤します。
| model.Maximize(sum( |
| data.shift_requests[n][d][s] * shifts[(n, d, s)] |
| for n in data.all_nurses |
| for d in data.all_days |
| for s in data.all_shifts |
| )) |
制約1: 1つのシフトに割り当てられる看護師は1⼈である。
AddExactlyOne() が、看護師ごとで1⽇1つのシフトのみ割り当てるようにするメソッドです。
| for d in data.all_days: |
| for s in data.all_shifts: |
| model.AddExactlyOne(shifts[(n, d, s)] for n in data.all_nurses) |
制約2: 毎⽇、各シフトは1⼈の看護師を割り当て、1⽇に複数のシフトに割り当ててはならない。
AddAtMostOne() が、変数 shifts の合計を最⼤1にするメソッドです。 看護師当たりの、⽇毎の全てのシフト合計が最⼤1になってほしいので、以下のようにプログラムを記述します。 つまり、合計1ならその⽇はシフトが⼊っており、0ならその⽇は休みになります。
| for n in data.all_nurses: |
| for d in data.all_days: |
| model.AddAtMostOne(shifts[(n, d, s)] for s in data.all_shifts) |
ソルバーを実⾏した結果は、以下のように出⼒されます。リクエスト通りにシフト割り当てがされた数を最後にカウントしています。
| 看護師1⼈当たりの, 7⽇間での最⼩シフト数: 4 |
| 看護師1⼈当たりの, 7⽇間での最⼤シフト数: 5 |
| 1⽇⽬: |
| シフト1: 看護師5 (非リクエスト) |
| シフト2: 看護師3 (リクエスト) |
| シフト3: 看護師4 (リクエスト) |
| (7⽇⽬まで同様、⻑くなるので省略) |
| シフトリクエストに合致した割り当て数: 13 (全体: 20) |
分かりやすく表にまとめたのが以下の画像のようになります。 ⾚⾊がリクエストとは異なるシフトが割り当てられた結果です。

プログラム全体
| from dataclasses import field |
| from typing import Dict, List, Tuple |
| from ortools.sat.python import cp_model |
| from ortools.sat.cp_model_pb2 import CpSolverStatus |
| from ortools.sat.python.cp_model import IntVar |
| from pydantic import StrictInt |
| from pydantic.dataclasses import dataclass |
| ShiftVar = Dict[Tuple[int, int, int], IntVar] |
| @dataclass |
| class Data: |
| """問題に関するデータ定義 |
| Attributes: |
| num_nurses (StrictInt): 地点間の距離の配列(メートル単位) |
| num_shifts (StrictInt): ⾞両の数 |
| num_days (StrictInt): 全ての⾞両が経路の始点と終点となるインデックス |
| shift_requests (List[List[List[int]]]): 看護師を割り当てたいシフトリクエスト |
| min_shifts_per_nurse (int): 看護師1⼈当たりの最⼩シフト数 |
| max_shifts_per_nurse (int): 看護師1⼈当たりの最⼤シフト数 |
| """ |
| num_nurses: StrictInt |
| num_shifts: StrictInt |
| num_days: StrictInt |
| shift_requests: List[List[List[int]]] = field(default_factory=list) |
| min_shifts_per_nurse: int = field(init=False) |
| max_shifts_per_nurse: int = field(init=False) |
| def __post_init__(self): |
| self.min_shifts_per_nurse = (self.num_shifts * self.num_days) // self.num_nurses |
| print(f"看護師1⼈当たりの, {self.num_days}⽇間での最⼩シフト数: {self.min_shifts_per_nurse}") |
| if self.num_shifts * self.num_days % self.num_nurses == 0: self.max_shifts_per_nurse = self.min_shifts_per_nurse |
| else: |
| self.max_shifts_per_nurse = self.min_shifts_per_nurse + 1 |
| print(f"看護師1⼈当たりの, {self.num_days}⽇間での最⼤シフト数: {self.max_shifts_per_nurse}\n") |
| @property |
| def all_nurses(self) -> range: |
| return range(self.num_nurses) |
| @property |
| def all_shifts(self) -> range: |
| return range(self.num_shifts) |
| @property |
| def all_days(self) -> range: |
| return range(self.num_days) |
| def create_data_model() -> Data: |
| # シフトリクエストの定義 |
| # [看護師1:[1⽇⽬:[シフト1, シフト2, シフト3], ..., 7⽇⽬:[シフト1, シフト2, シフト3], ...], |
| # ..., |
| # 看護師5:[1⽇⽬:[シフト1, シフト2, シフト3], ..., 7⽇⽬:[シフト1, シフト2, シフト3], ...]] |
| shift_requests = [ |
| [[0, 0, 1], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 1]], |
| [[0, 0, 0], [0, 0, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [0, 0, 0], [0, 0, 1]], |
| [[0, 1, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0], [0, 1, 0], [0, 0, 0]], |
| [[0, 0, 1], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0]], |
| [[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0]] |
| ,] |
| # 看護師5⼈, シフト3つ, 7⽇分 |
| data = Data(num_nurses=5, num_shifts=3, num_days=7, shift_requests=shift_requests) |
| return data |
| def print_solution(solver: cp_model.CpSolver, status: CpSolverStatus.ValueType, data: Data, shifts: ShiftVar): |
| if status == CpSolverStatus.OPTIMAL: |
| for d in data.all_days: |
| print(f"{d+1}⽇⽬:") |
| for s in data.all_shifts: |
| for n in data.all_nurses: |
| if solver.Value(shifts[(n, d, s)]) == 1: |
| if data.shift_requests[n][d][s] == 1: |
| print(f"シフト{s+1}: 看護師{n+1} (リクエスト)") |
| else: |
| print(f"シフト{s+1}: 看護師{n+1} (⾮リクエスト)") |
| print() |
| print( |
| f"シフトリクエストに合致した割り当て数: {int(solver.ObjectiveValue())}", |
| f"(全体: {data.num_nurses * data.min_shifts_per_nurse})", ) |
| else: |
| print("最適なソリューションが⾒つかりませんでした.") |
| def main(): |
| data = create_data_model() # データの取得 |
| model = cp_model.CpModel() # モデルの宣⾔ |
| # 変数の宣⾔ (割り当てわれたら1、そうでなければ0が設定される) |
| # n: 看護師, d: ⽇, s: シフト |
| shifts: ShiftVar = {} |
| for n in data.all_nurses: |
| for d in data.all_days: |
| for s in data.all_shifts: |
| # key: (n,d,s) のタプル, value: ブール変数 |
| shifts[(n, d, s)] = model.NewBoolVar(name=f"shift({n},{d},{s})") |
| # 制約: 1つのシフトに割り当てられる看護師は1⼈である。 |
| for d in data.all_days: |
| for s in data.all_shifts: |
| model.AddExactlyOne(shifts[(n, d, s)] for n in data.all_nurses) |
| # 制約: 看護師は1⽇当たり最⼤1回のシフトが割り当てられる。 |
| # つまり、1⼈の看護師が1⽇に2回以上シフトが割り当てられないようにする. |
| for n in data.all_nurses: |
| for d in data.all_days: |
| model.AddAtMostOne(shifts[(n, d, s)] for s in data.all_shifts) |
| # シフトを出来るだけ均等に割り当てるための制約を設定する. |
| for n in data.all_nurses: |
| num_shifts_worked = 0 # 看護師1⼈当たりの、シフト数*⽇数分の変数 |
| for d in data.all_days: |
| for s in data.all_shifts: |
| num_shifts_worked += shifts[(n, d, s)] |
| # 制約: 全ての看護師は, 最⼩シフト数以上のシフト数を割り当てられる. |
| model.Add(data.min_shifts_per_nurse <= num_shifts_worked) |
| # 制約: 全ての看護師は, 最⼤シフト数以下のシフト数を割り当てられる. |
| model.Add(num_shifts_worked <= data.max_shifts_per_nurse) |
| # ⽬的: シフトリクエストを1に設定したシフトに、出来るだけ看護師を割り当てたい. |
| model.Maximize(sum( |
| data.shift_requests[n][d][s] * shifts[(n, d, s)] |
| for n in data.all_nurses |
| for d in data.all_days |
| for s in data.all_shifts |
| )) |
| solver = cp_model.CpSolver() |
| # ソルバーを実⾏ |
| status = solver.Solve(model) |
| print_solution(solver, status, data, shifts) |
| if __name__ = "__main__": |
| main() |
⾞両ルートに関する問題
公式サイト: ⾞両ルートに関する問題
⾞両ルート問題 (VRP: Vehicle Routing Problem) は、複数の⾞両が決まった地点を訪問するとき、⾞両ごとに最適な経路を⾒つける問題です。 最適な経路とは、⾞両の積載量や特定の⾞両のみ制限時間があったりといった制約が無い限りは、「全⾞両のうち最⻑となる経路を最も短くする」ことを⽬標にするのがおすすめされています。
問題の定式化
以下のような、4台の⾞両が地点0から出発し、⻘⾊の地点を全て訪問する問題を考えます。
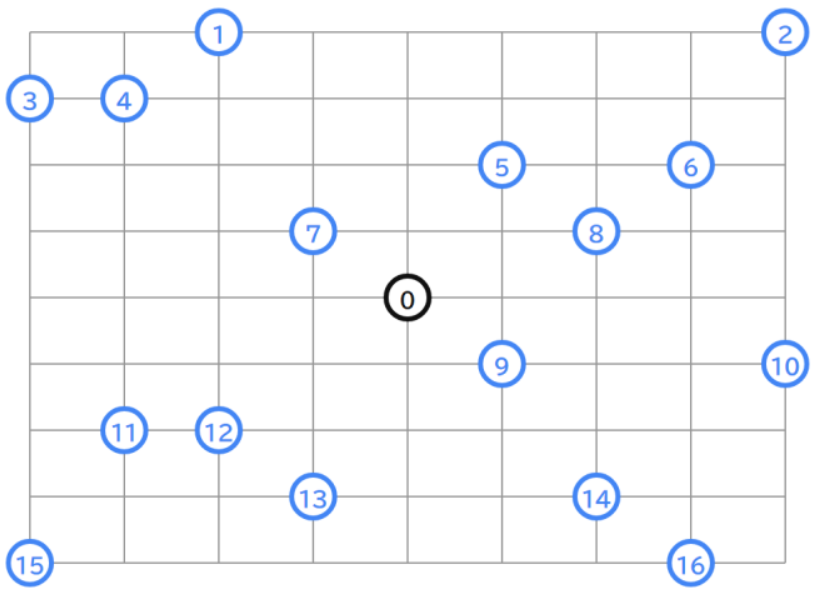
(https://developers.google.com/optimization/routing/vrp より引⽤)
また、各地点の座標は以下のように与えられています。
| [(456, 320), # 地点 0 - 開始地点 |
| (228, 0), # 地点 1 |
| (912, 0), # 地点 2 |
| ... # ⻑くなるので省略。全座標は公式ガイドに記載されています。 |
| (798, 640)] # 地点 16 |
ソルバーに⼊⼒するデータは、2地点間の距離(メートル単位)であり、地点の座標ではありません。そのため、 座標から距離を計算 する必要があります。ガイドでは、事前に計算されたデータが与えられているので、それをそのまま使⽤することにします。
次に問題を「⽬的」「制約」に定式化します。⾞両ルート問題は、これまでの例と違ってある程度「お約束」の定式化があり、数式に落とし込むというよりOr-Toolsで想定された定式化に従うイメージとなります。
- ⽬的: 4台の⾞両が全地点を訪問するとき、全⾞両のうち最⻑となる経路を最も短くする。
- 制約: 距離に関する制約
⽬的: 4台の⾞両が全地点を訪問するとき、全⾞両のうち最⻑となる経路を最も短くする。
この⽬的を満たすため、まずは以下のように コスト評価 のメソッドを定義します。これは、全ての⾞両において2点間を移動するときのコストを評価します。
| routing.SetArcCostEvaluatorOfAllVehicles(evaluator_index=transit_callback_index) |
ちなみにこの routing というのが、問題を定式化したモデルとなります。そして、次に 距離に関する制約を課します。以下の AddDimension が、制約の追加メソッドとなり、引数にパラメータを追加していきます。
| routing.AddDimension( |
| evaluator_index=transit_callback_index, # コールバック関数の登録 |
| slack_max=0, # ⾞両の待ち時間。今回は0とした。 |
| capacity=3000, # ⾞両の最⼤移動距離(メートル)は3000とした。 |
| fix_start_cumul_to_zero=True, # 累積時間は0から開始する。 |
| name=dimension_name, # 制約名 |
| ) |
最後に、以下のように探索パラメータの設定をして、ソルバーを実⾏します。Or-Toolsにおけるこの探索⼿法を「ヒューリスティック」といい、これは厳密解を求めるのでなく厳密解に近い解答を発見するものです。ヒューリスティックによって、厳密解を発⾒するより大幅に時間を短縮できるメリットがあります。探索パラメータは複数⽤意されていますが、今回は公式の例に合わせます。
| # 探索パラメータの設定 |
| search_parameters: RoutingSearchParameters = pywrapcp.DefaultRoutingSearchParameters() |
| # 最初のソリューションを発⾒するための戦略を設定 |
| search_parameters.first_solution_strategy = routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC |
| # ソルバーの実⾏ |
| solution = routing.SolveWithParameters(search_parameters=search_parameters) |
プログラム全体
| from typing import List |
| from ortools.constraint_solver import pywrapcp, routing_enums_pb2 |
| from ortools.constraint_solver.pywrapcp import RoutingIndexManager, RoutingModel, Assignment, RoutingDimension |
| from ortools.constraint_solver.routing_parameters_pb2 import RoutingSearchParameters |
| from pydantic import StrictInt, Field |
| from pydantic.dataclasses import dataclass |
| @dataclass |
| class Data: |
| """問題に関するデータ定義 |
| Attributes: |
| distance_matrix (List[List[int]]): 地点間の距離の配列(メートル単位) num_vehicles (StrictInt): ⾞両の数 |
| depot (StrictInt): 全ての⾞両が経路の始点と終点となるインデックス |
| """ |
| num_vehicles: StrictInt depot: StrictInt |
| distance_matrix: List[List[int]] = Field(default_factory=list) |
| def create_data_model() -> Data: |
| """ルート最適化問題⽤のデータを作成""" |
| # 距離⾏列の定義 |
| # ルート最適化では、地点間の距離を扱う。座標ではないことに注意。事前に座標間の距離を求める必要がある。 |
| # この例では、座標間の距離⾏列を事前に計算したものとする。 |
| distance_matrix = [ |
| [0, 548, 776, 696, 582, 274, 502, 194, 308, 194, 536, 502, 388, 354, 468, 776, 662], |
| [548, 0, 684, 308, 194, 502, 730, 354, 696, 742, 1084, 594, 480, 674, 1016, 868, 1210], |
| [776, 684, 0, 992, 878, 502, 274, 810, 468, 742, 400, 1278, 1164, 1130, 788, 1552, 754], |
| [696, 308, 992, 0, 114, 650, 878, 502, 844, 890, 1232, 514, 628, 822, 1164, 560, 1358], |
| [582, 194, 878, 114, 0, 536, 764, 388, 730, 776, 1118, 400, 514, 708, 1050, 674, 1244], |
| [274, 502, 502, 650, 536, 0, 228, 308, 194, 240, 582, 776, 662, 628, 514, 1050, 708], |
| [502, 730, 274, 878, 764, 228, 0, 536, 194, 468, 354, 1004, 890, 856, 514, 1278, 480], |
| [194, 354, 810, 502, 388, 308, 536, 0, 342, 388, 730, 468, 354, 320, 662, 742, 856], |
| [308, 696, 468, 844, 730, 194, 194, 342, 0, 274, 388, 810, 696, 662, 320, 1084, 514], |
| [194, 742, 742, 890, 776, 240, 468, 388, 274, 0, 342, 536, 422, 388, 274, 810, 468], |
| [536, 1084, 400, 1232, 1118, 582, 354, 730, 388, 342, 0, 878, 764, 730, 388, 1152, 354], |
| [502, 594, 1278, 514, 400, 776, 1004, 468, 810, 536, 878, 0, 114, 308, 650, 274, 844], |
| [388, 480, 1164, 628, 514, 662, 890, 354, 696, 422, 764, 114, 0, 194, 536, 388, 730], |
| [354, 674, 1130, 822, 708, 628, 856, 320, 662, 388, 730, 308, 194, 0, 342, 422, 536], |
| [468, 1016, 788, 1164, 1050, 514, 514, 662, 320, 274, 388, 650, 536, 342, 0, 764, 194], |
| [776, 868, 1552, 560, 674, 1050, 1278, 742, 1084, 810, 1152, 274, 388, 422, 764, 0, 798], |
| [662, 1210, 754, 1358, 1244, 708, 480, 856, 514, 468, 354, 844, 730, 536, 194, 798, 0], |
| ] |
| # 距離⾏列と⾞両数とデポ(⾞両の開始/終了地点インデックス)を設定 |
| data = Data(distance_matrix=distance_matrix, num_vehicles=4, depot=0) |
| return data |
| def print_solution(data: Data, manager: RoutingIndexManager, routing: RoutingModel, solution: Assignment) -> None: |
| """ソリューションをコンソール出⼒する |
| Args: |
| data (Data): 最適化問題⽤データ |
| manager (RoutingIndexManager): インデックスマネージャー |
| routing (RoutingModel): ルーティングモデル |
| solution (Assignment): ソリューション |
| """ |
| for vehicle_id in range(data.num_vehicles): |
| index = routing.Start(vehicle=vehicle_id) # ⾞両の始点インデックスを取得 |
| out_text = f"⾞両{vehicle_id+1} の巡回経路:\n" # コンソール出⼒⽤⽂字列変数 |
| route_distance = 0 # 各⾞両の合計移動距離 |
| while not routing.IsEnd(index=index): |
| out_text += f" {manager.IndexToNode(index)} ->" |
| previous_index = index |
| index = solution.Value(routing.NextVar(index)) |
| # 2点間の移動距離を取得し、合計距離に追加する |
| route_distance += routing.GetArcCostForVehicle( |
| from_index=previous_index, to_index=index, vehicle=vehicle_id |
| ) |
| out_text += f" {manager.IndexToNode(index)}\n" # 最後のノード(デポになるはず) |
| out_text += f"巡回経路の合計距離: {route_distance}m\n" |
| print(out_text) |
| def main(): |
| data = create_data_model() # 問題⽤データの取得 |
| # 経路最適化では、routingモデル(ソルバー)と, ソルバー内部で使⽤するIndexと⼈間が認識する地点(Node)を紐づけるmanagerを定義する. |
| # RoutingIndexManager は *args (可変⻑)を引数とするため、ラッパー関数を作成すると良さそう。 |
| manager: RoutingIndexManager = pywrapcp.RoutingIndexManager( |
| len(data.distance_matrix), # 地点数 |
| data.num_vehicles, # ⾞両数 |
| data.depot, # ⾞両の巡回開始/終了地点のインデックス |
| ) |
| routing: RoutingModel = pywrapcp.RoutingModel(manager) |
| def distance_callback(from_index: int, to_index: int) -> int: |
| """距離のコールバック関数 |
| Args: |
| from_index (int): 出発地点のソルバー⽤インデック |
| to_index (int): 到着地点のソルバー⽤インデックス |
| Returns: |
| int: 距離⾏列から取得した、2点間距離 |
| """ |
| from_node = manager.IndexToNode(from_index) |
| to_node = manager.IndexToNode(to_index) |
| return data.distance_matrix[from_node][to_node] |
| # 上記で作成したコールバック関数をroutingに登録 |
| transit_callback_index = routing.RegisterTransitCallback(distance_callback) |
| # 2点間の移動コストの設定(円弧コスト) |
| # 今回の例は距離⾏列のみ与えられているので、考慮されるコストは距離のみとなる。 |
| routing.SetArcCostEvaluatorOfAllVehicles(evaluator_index=transit_callback_index) |
| # 移動距離に関する制約 |
| dimension_name = "Distance" |
| routing.AddDimension( |
| evaluator_index=transit_callback_index, # コールバック関数 |
| slack_max=0, # ⾞両の待ち時間. 今回は0とした. |
| capacity=3000, # ⾞両の最⼤移動距離(メートル)は3000とした. |
| fix_start_cumul_to_zero=True, # 累積時間は0から開始 |
| name=dimension_name, # 制約の名前 |
| ) |
| distance_dimension: RoutingDimension = routing.GetDimensionOrDie(dimension_name=dimension_name) |
| # 距離に関する制約に⼤きな係数をかけることで、ソルバーは出来るだけ各⾞両の最⻑移動距離を短くしようとする。 |
| distance_dimension.SetGlobalSpanCostCoefficient(coefficient=100) |
| # 探索パラメータの設定 |
| search_parameters: RoutingSearchParameters = pywrapcp.DefaultRoutingSearchParameters() |
| # 最初のソリューションを発⾒するための戦略を設定する。詳細は以下のリンク参照。 |
| # https://developers.google.com/optimization/routing/routing_options? hl=ja#first_solution_strategy |
| # 今回は PATH_CHEAPEST_ARC という戦略を使⽤している。 |
| search_parameters.first_solution_strategy = routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC |
| # ソルバーの実⾏ |
| solution = routing.SolveWithParameters(search_parameters=search_parameters) |
| if solution: |
| print_solution(data=data, manager=manager, routing=routing, |
| solution=solution) |
| else: |
| print("No solution found.") |
| if __name__ == "__main__": |
| main() |
まとめ
数理最適化は、どうしても数学の要素が強く数式を読み解いていったり、又は数式を自分で作成していくのは難しいと思います。また、公式ガイドでもある程度の事前知識があることを前提とした内容となっており、そこも敷居が高い原因はないかと思います。
この記事で少しでも、最適化のイメージを掴んでいただければ幸いです。




