技術研究所の(あ)です。
機械学習を使った画像分類を用いた医療系の共同研究をいろいろやったりしてます。
画像分類などの分類問題の性能評価指標って、なんかいろいろ出てくるよねー、それって何がどう違うの? ということで以前、感度とか特異度とかの話を書きました。今回はその続編ということで「F値」の話を書きます。
そしてそこで出てくる、「調和平均」って何者? という話も書きます。
(この記事は「CRESCO Advent Calendar 2019」最終日の記事です)
分類問題の性能を評価しようと思うと、感度や特異度だとある指標の数値が同じでも有病率しだいでけっこう様子が変わってしまう、というのは前回書きました。そのため、複数の指標を使うことになるわけですが、そうすると「手法A と手法B を較べると、こっちの指標は A がよいけれど、あっちの指標は B がよいので、総合的にどちらを選べば…」というようなことが起こります。
そこで、一つの値でもう少し総合的なことを表せる指標がほしくなるわけですが、そんな指標の一つが F値 (F-score, F-value) です。重み付けを加えたバリエーション (Fβ値) も存在するので、区別するために F1 値ということもあります。この F値がどういう計算で求められるかというと、端的に
F値: 感度と適合度の調和平均
と表されます。多くの解説では、この定義か、これを式変形したもの、あるいは感度などの定義に遡って真陽性 True Positive (TP) の数や偽陽性 False Positive (FP) の数、偽陰性 False Negative (FN) の数に置き換えた式変形を提示して終わってしまっています (表記のバリエーションのいくつかを記事の最後のほうに挙げておきます)。「調和平均」についても「逆数の平均の逆数」ということや、計算のしかたくらいしか書かれていません。
それって何なの? どういう意味合いなの? というのが気になる人もいるでしょう。以下、そのあたりの解説をしていきます。まず、調和平均についてです。
平均にも実はいろいろな種類があります。多くの人にとって、「平均」と言ってまず頭に思い浮かぶのは下の図のような均し方でしょう。
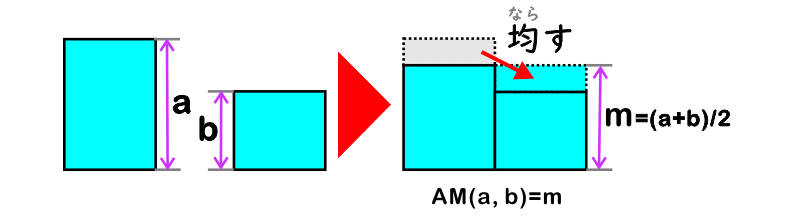
a と b の平均 m は a と b を足して 2 で割ったもの、m = (a + b) / 2 です。これを、相加平均もしくは算術平均 (Arithmetic Mean) といいます。以下、AM(a, b) = m のように表します。a グラムの食塩と b グラムの食塩とを混ぜて等しく二つに分けたときの食塩の重さは m グラムです。
上の図では a と b という「量」の平均をとっていますが、全体が同じであればそれに対する比率で表すこともできます。
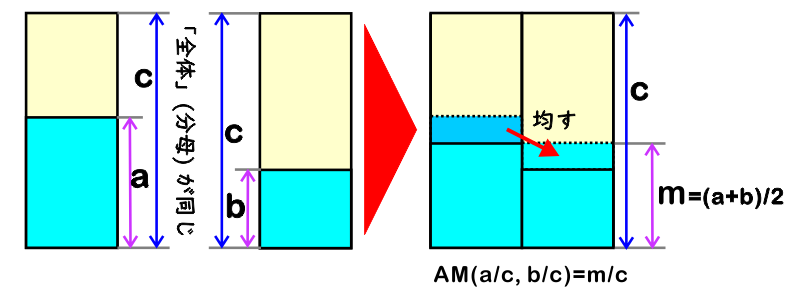
AM(a/c, b/c) = m/c、です。同じ重さの (濃度は違う) 食塩水を混ぜたときの濃度などがこれに当たります。
a グラムの食塩が溶けている食塩水 c グラム (濃度 a/c) と、
b グラムの食塩が溶けている食塩水 c グラム (濃度 b/c) とを混ぜると、
濃度 m/c の食塩水が 2×c グラムできます。
比率のようなものを扱う場合、このように「全体」(= 分母に来る数量) が同じものに対しては算術平均が適切です。
これに対し、分子にくる数量 (全体のうちの着目している部分など) が同じものに対しては調和平均 (Harmonic Mean) が適切です。
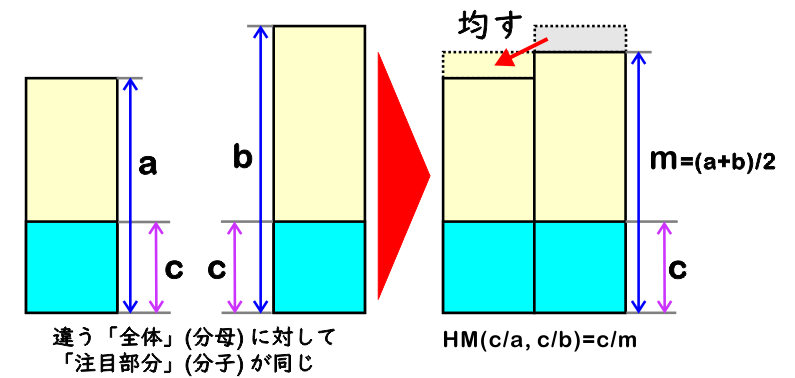
c グラムの食塩が溶けている食塩水 a グラム (濃度 c/a) と、
c グラムの食塩が溶けている食塩水 b グラム (濃度 c/b) とを混ぜると、
濃度 c/m の食塩水が a + b グラムできます (等しく二つに分けると (a + b) / 2 グラムずつです)。
A と B の調和平均が M だとすると (以下、HM(A, B) = M と表します)、(1/A + 1/B) / 2 = 1/M という関係があります。M は、A と B の「逆数の平均の逆数」です。上の図だと、HM(c/a, c/b) = c/m です。
算術平均の図と調和平均の図を見比べると、だいぶ似ています。実際、違うのは、a や b に対して c が大きいか小さいか、だけです。並べてみて、算術平均のほうの色をひっくり返すと、よりそっくりさ加減が判ります。
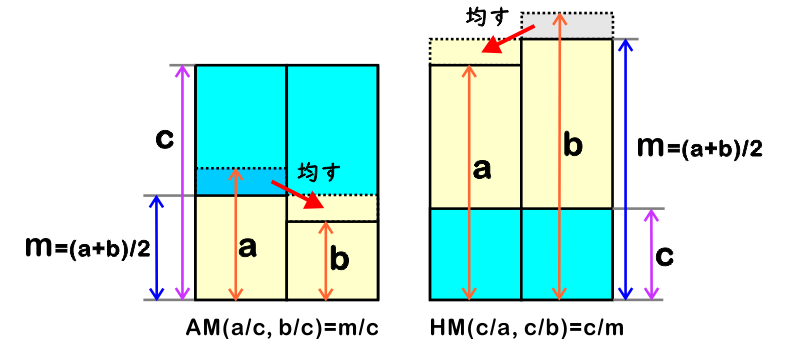
式のほうも、数値部分を全部逆数 (分子と分母を逆) にして、AM←→HM を取り替えると同じになってます。(a, b, c が 0 でないとき) AM(a/c, b/c) = m/c ならば HM(c/a, c/b) = c/m で、逆も真です。
「分母が同じもの (として合わせる) か、分子が同じもの (として合わせる) かの違いだけで、
算術平均と調和平均の本質は同じものだったんだよッ!!!」
といっても過言ではないくらいです (「な、なんだってーッ!!」)。
「調和平均は算術平均の裏返し」と表現してもよいでしょう。
まあ、「調和平均は、逆数の算術平均の逆数」なので当たり前といえば当たり前ですが、あらためて考えてみるとちょっと意外な感じです。
前節では例として食塩水の濃度で説明しましたが、他に調和平均が用いられる場面を見てみましょう。
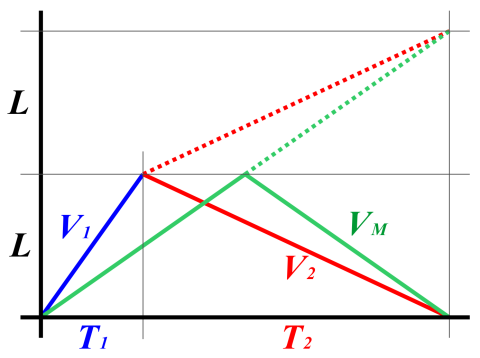
まず、よく取り上げられる事例の「往復での平均速度」です。「距離 L(km) 離れた二地点を往復するときに、往きは V1(km/h) の速度で、かえりは V2(km/h) の速度で移動しました。平均速度は?」という問題です。
往きにかかった時間を T1(h) とすると、T1 × V1 = L なので、V1 = L / T1 です。同様にかえりにかかった時間を T2(h) とすると、V2 = L / T2 です。おお、分子の L が一緒ですね! ということで、調和平均を使って VM = HM(V1, V2) とすると、
VM×(T1 + T2) = 2×L
となる「平均速度」として適切な値が計算できます。
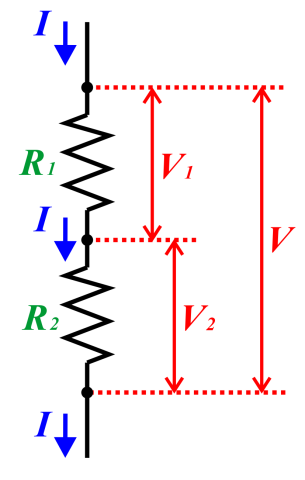
次に、オームの法則の事例です。電気回路で抵抗値 R1(Ω)、R2(Ω)の抵抗を二つ直列につなぐと、全体の抵抗は R1+R2(Ω) になって、一本当たりの平均抵抗値は Rm = AM(R1, R2) = (R1+R2)/2 (Ω) とみなせます。二つを並列につなぐと、全体の抵抗は 1/(1/R1 + 1/R2)(Ω) (逆数の和の逆数) になります。抵抗値 RM = HM(R1, R2) = 2/(1/R1 + 1/R2) (逆数の算術平均の逆数) の抵抗二本が並列につながっているのと同じです。
細かく見ていきましょう。
全体に掛かる電圧を V (ボルト)、流れる電流の総量を I (アンペア) とします。それぞれの抵抗に掛かる電圧を V1, V2、流れる電流を I1, I2 とします。オームの法則 (電圧V = 電流I × 抵抗値R) から、
V1 = I1×R1
V2 = I2×R2
です。直列につないだ場合は電圧は二本の抵抗で分配され、電流は同じになる、すなわち V1+V2=V, I1=I2=I なので
V1 = I×R1 → R1 = V1/I
V2 = I×R2 → R2 = V2/I
となり「分母が同じ」になります。よって平均の抵抗値を求めるには算術平均が適切です。
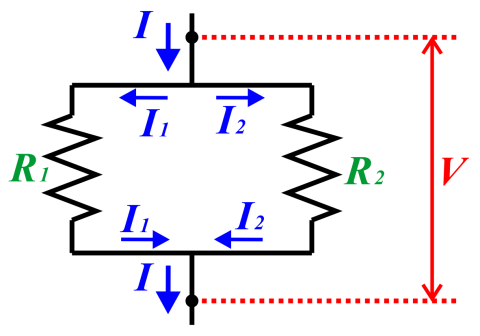
並列につないだ場合は、今度は双方に同じ電圧が掛かり、電流は分配される、すなわち V1=V2=V, I1+I2=I なので、
V = I1×R1 → R1 = V/I1
V = I2×R2 → R2 = V/I2
となり「分子が同じ」(!) になります。よって平均の抵抗値を求めるには調和平均が適切です。ちゃんときれいに辻褄があっていますね。
最初のほうで書いたとおり、F値とは「感度と適合度の調和平均」です。とすると、何か「分子が同じ」はずですね。確認しましょう。感度 (recall) と適合度 (precision) の定義をおさらいがてら見てみると…、
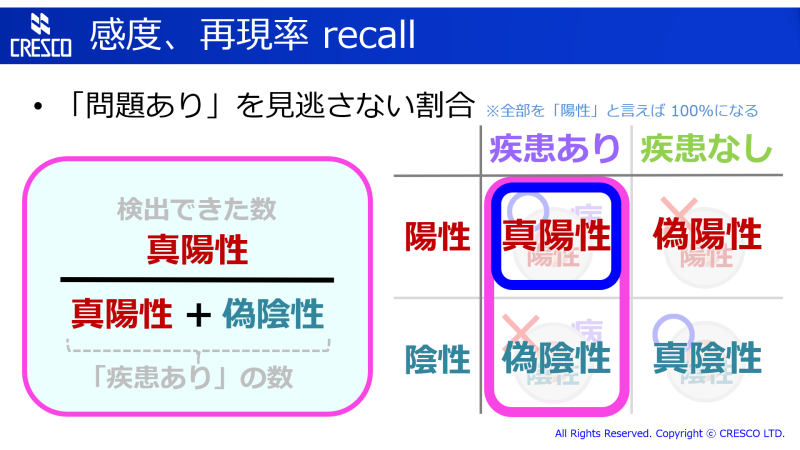
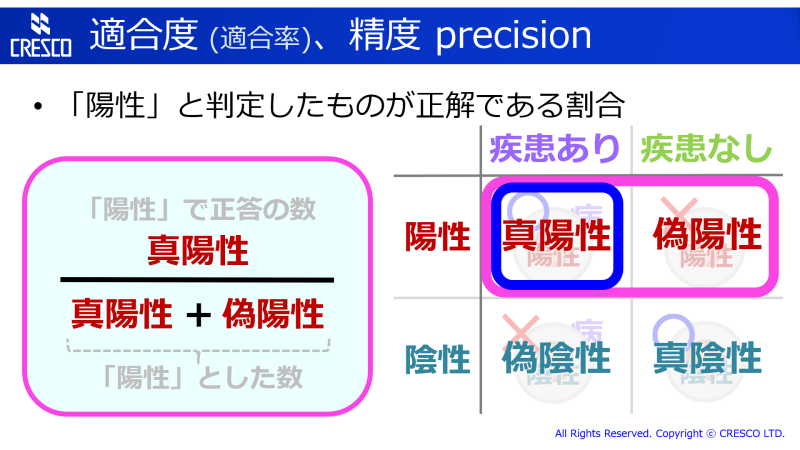
はい、分子が両方とも「真陽性」で同じですね。分母の数字の性質がお互いちょっと違うのでは? という点がやや引っかかりますが、算術平均よりは調和平均を取るほうが適切であろう、と判断できます (引っかかる点に関して「感度と適合度の重みは同じではない」ということに対応するのが Fβ値になります)。
最後に、F値の計算式のバリエーションをいくつか載せておきます。ちなみに F値 の “F” は何か特別な意味があるのかと思ったら、元を辿るとどうも単なる “Function” (関数) の “F” らしい、です (えー)。

一つの値で表す分類問題の評価指標には他に AUC (Area Under the Curve) というものもあります。「値」ではないですが、閾値を変動させたときの変化をみる ROC Curve (Receiver Operation Characteristic Curve) (AUC の計算にはこれを使う) や Precision-Recall Curve などもあります。
また、平均にも、算術平均 (相加平均) と調和平均以外にも、幾何平均 (相乗平均) などもあります。これらの話はまた別の機会に…。




