感度、特異度、精度、再現率、適合度、などなど…
何がどう違うのでしょう? 何でたくさんあるのでしょう?
もちろん本やウェブで調べれば出てきますが、意外とすっきり簡潔に解りやすくまとめた資料がありません。いろいろな人に説明せねばならない機会も増えたし、それではということで自分で説明図などを作ってみました。
確認のためなどに使いたい方も多いかと思いますので、見やすいよう、最初にまとめの図を載せてしまいます:-)
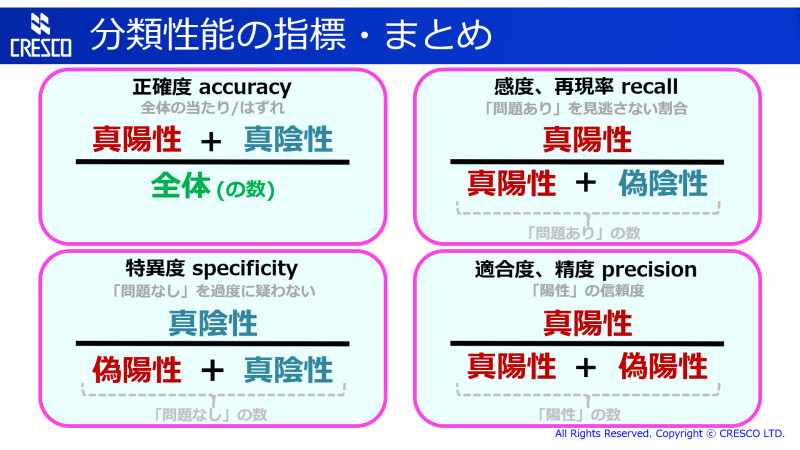
大学での講義などでも使ってますので、スライドのレイアウトになってます。
以下、ここへ至る説明をしていきます。
さて、こういう話の場合、まずはどういう状況を想定しているのかをはっきりさせないといけません。ここでの状況は、以下のようなものです。
- 検査や分類の対象になるものが (多数) ある:
眼科疾患の話だと「一個一個の眼」になります - 検査や分類で検出したいもの (多くの場合何らかの問題を持つもの) がある:
眼科疾患の話だと「疾患がある眼」になります
例を絵にしてみるとこんな感じです。
いくつかの眼があって、その中のいくつかに疾患が隠れています。
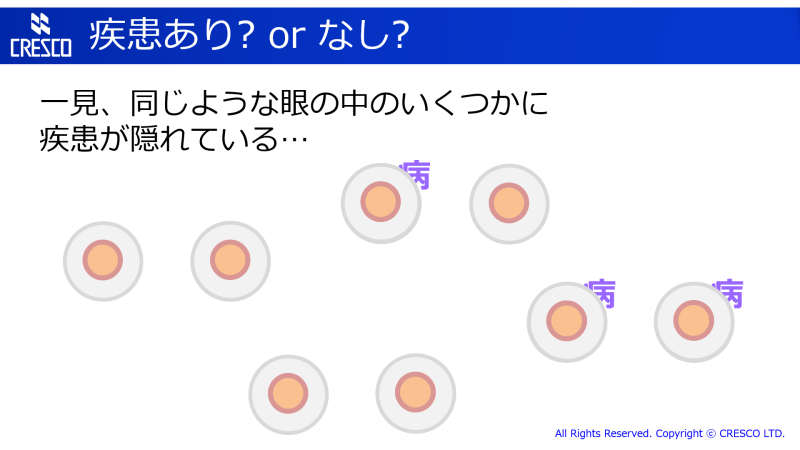
そして、もう一つは検査や分類のほうの設定。
- 検査や分類は、対象が問題を持つ (疾患がある) か否かを 0/1 で判定する:
問題を持つ可能性を確率で示す検査や分類もありますが、ここではきっちりと有無で判定するものとします - 検査や分類は通常、完全ではなく、判定できるのはあくまで対象が問題 (疾患) を持つ疑いがあるか否かである:
あたりまえではありますが、これをちゃんと覚えておかないと話がとてもこんがらがります
問題の疑いありと判断されたものを「陽性」(positive)、そうでないものを「陰性」(negative) と (判断された・結果が出た) と言います。先程の例に検査を適用してみた様子がこんなだったとしましょう。
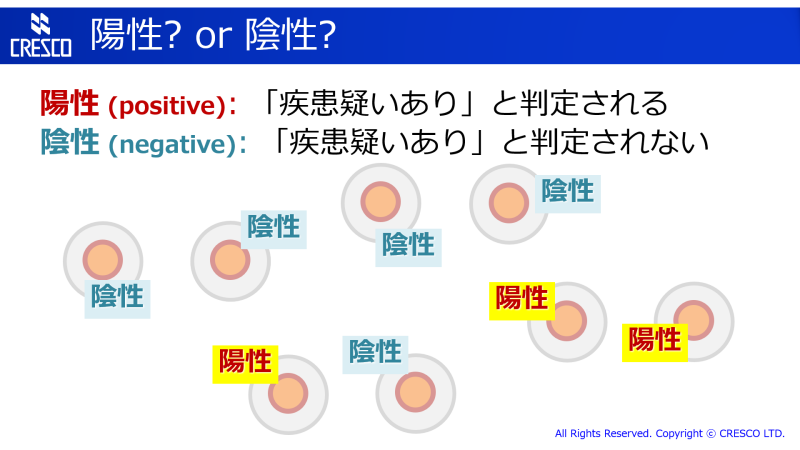
判定が全て「正答」で、疾患があるものが全て陽性、疾患がないものが全て陰性になればよいのですが、完全ではないのでそうはいきません。疾患があるのに陰性と判定されるもの、疾患がないのに陽性と判定されるもの、すなわち「誤答」となるものが出てきます。
これらを表すために、「正答」に「真」、「誤答」に「偽」という接頭辞を用います。つまり、
・「陽性」で「正答」(疾患がある) ものを「真陽性」
・「陽性」で「誤答」(疾患がない) ものを「偽陽性」
・「陰性」で「正答」(疾患がない) ものを「真陰性」
・「陰性」で「誤答」(疾患がある) ものを「偽陰性」
とします。
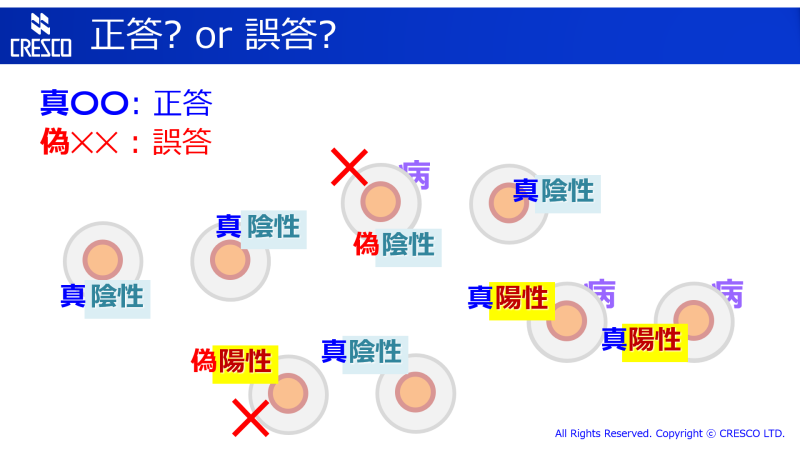
実際の疾患の有無と、陽性・陰性で 2×2 の表にしてみると、
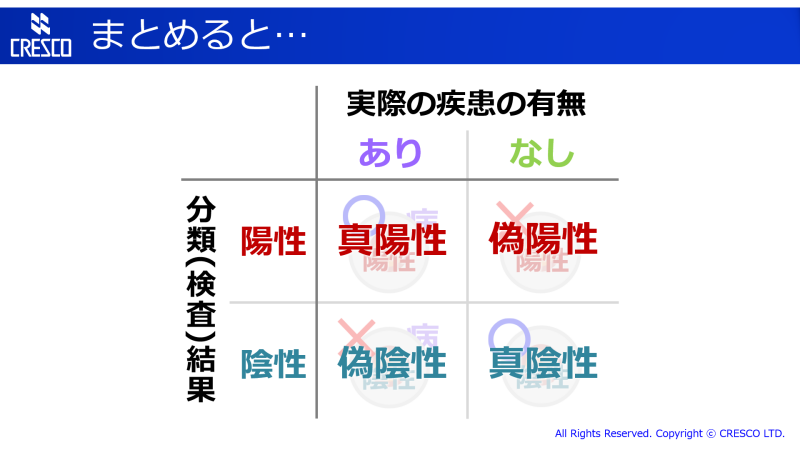
このようになります。判定と疾患の有無が一致する左上から右下への対角線部分が「正答」なので、「真」がついているということになります。
誤答には偽陽性と偽陰性の二種類があります。どちらも「判定が間違っている」という点では同じですが、「判定を間違えたことによる影響」の出方が異なります。偽陽性は疾患のない人に「疾患があるかも」と心配を掛けたりさらなる検査の手間を掛けさせたりするだけ (「だけ」と言ってしまうと語弊があるかもしれませんが…) ですが、偽陰性は疾患を見逃し、治療を遅れさせることになります。
ここに、さまざまな指標が登場する理由があります。状況や深刻度などにもよりますが、疾患の判定であれば、多少疾患なしの人を誤判定したとしても、見逃しをなるべく減らしたいでしょう。だからといって、疾患が実際にはない人にまでやたらめったら「疾患があるかも」といってしまう判定では役に立ちません。
重要なのは、状況や必要に応じたバランスです。それを見るために、複数の指標を使います。
さてさてようやくそれぞれの指標の意味合いと、どういう計算をするかの説明です。言葉は違うけど同じもの、というのもあります (ややこしい…)。
これは、誤答の種類を考えない、全体の正答率・正解率です。正答のもの (真陽性・真陰性) の数を、全体の数で割ります (図の、青で囲んだ部分が分子、紫で囲んだ部分が分母になります)。いちばん解りやすい指標ですね。機械学習で学習させる途中に学習度合いをチェックするのにも使います。
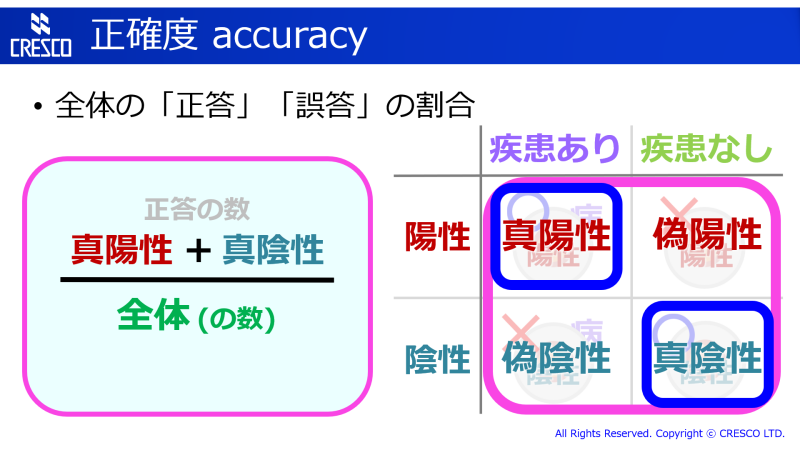
問題 (疾患) のあるものを見逃さない割合です。検出できた (陽性の) 対象の数を、疾患ありの総数 (真陽性 + 偽陰性) で割ります。前述のように、疾患の有無の判定などでは最重要の指標と言ってもよいでしょう。
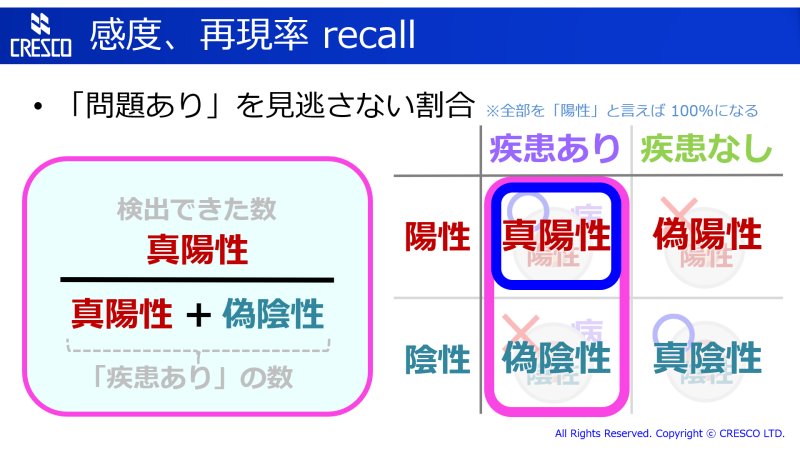
問題 (疾患) のないものをむやみやたらと疑わない、ということを表す指標です。ちゃんと陰性と判定できた数を、疾患のないものの数で割ります。この指標も高いに越したことはありませんが、場合によっては特異度を下げてでも感度を上げたいかもしれません。
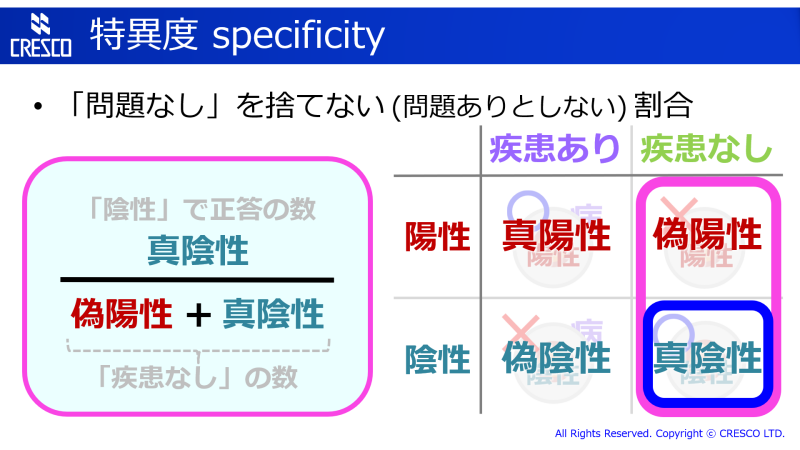
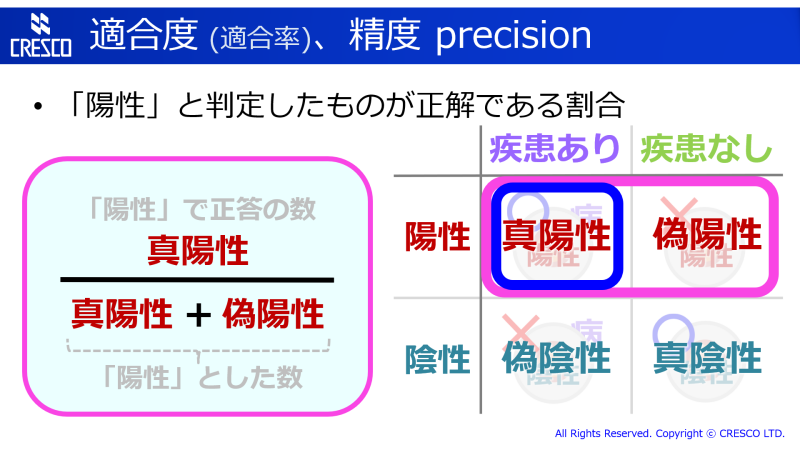
陽性と判定されたもののうち、どれだけ実際に問題 (疾患) があるかを表す、「むやみやたらと疑わない」の別方向の指標です。もしくは「陽性」判定の信憑性を表す、と言ってもよいでしょう。陽性かつ疾患あり (真陽性) のものの数を、陽性のものの数で割ります。陽性適中率、と呼ばれることもあります。
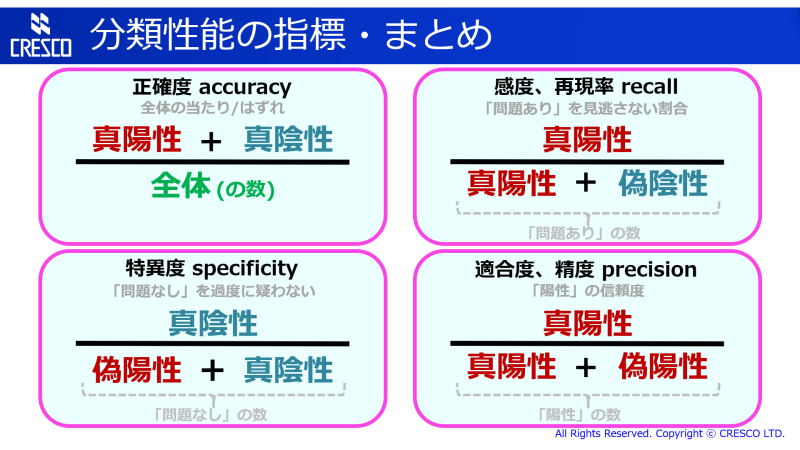
ここで紹介した四つの指標の内容をまとめたものを再掲します。
さて、これらの指標の数値は、検査や分類の方法だけでは全部は定まりません。たとえば、疾患の判定の場合であれば「有病率」が正確度や適合度に影響します。これは、実際の対象の中に、どれくらいの割合で疾患 (問題) ありが含まれるか、という割合です。
たとえば、疾患A を判定する検査αが、感度99%・特異度80% だったとしましょう。
そして、疾患A を持つ人の割合が 10000人中5000人もいたとします。残り半分の 5000人は疾患A を持っていません。疾患を持つ 5000人のうち、検査αで「陽性」と判定されるのは 5000×0.99 で 4950人です (いや実際は統計的な話なので数字は前後するでしょうけれどそれはここでは置いておきます)。 見逃される偽陰性の人の数は 5000-4950=50人です。疾患のない 5000人のうち、5000-5000×0.80=1000人は偽陽性の判定です。
陽性の人は合計 5950人、陰性の人は合計4050人。まとめの図を見たりしつつ計算してみて下さい。
適合度: 83%、正確度: 90% になります。
50%の有病率なんていうのはそうそうないでしょうから、今度は10%の場合を考えてみましょう。疾患A を持つ人の割合は 10000人中1000人になります。この 1000人のうち、検査αで「陽性」と判定されるのは 1000×0.99 で 990人です。一方、疾患を持たない 9000人のうち、検査αで「陽性」と判定されるのは 9000 – 9000×0.80 で 1800人です。
真陽性 990人に対し偽陽性 1800人。なんと、陽性の人のうち、本当は疾患のない人の数が、実際に疾患のある人の数の倍近くいます。
先程の有病率50% の場合は実際に疾患のある人の数のほうが圧倒的に多かったのに!
真陽性、真陰性、偽陽性、偽陰性それぞれの数を計算して、適合度と正確度を求めてみて下さい。さきほどと較べて適合度は 35% と大きく下がります。正確度のほうはそれほどまでではないですが、82% に下がります。
さらに有病率が低いとどうなるでしょう? 疾患A を持つ人の割合が 10000人中100人、すなわち有病率が 1%だと……。
検査αで真陽性になるのが 99人、対して偽陽性は 1980人。適合度は 5%まで落ちてしまいます。正確度はご自分で計算してみて下さい。
検査α自体は同じなのに、有病率でこれだけ正確度や適合度は変わります。疾患の深刻度などにも応じて、各種指標のバランスのよい検査が求められるというのも頷けるかと思います。




