[前回までのあらすじ]
実は調和平均とは算術平均の裏返しであった。分母にあたるものが同じ場合の平均を考えるのに算術平均が適切であるなら、分子にあたるものが同じ場合の平均を考えるには調和平均が適切で、分子分母が逆転している以外は同じと言っても過言ではなかったのだ…。
技研の(あ)です。前回は F値と、その計算に使われる調和平均 (Harmonic Mean) ってどういうもの? という話を書きました。ところでなんでこれって「調和」平均って言うんでしょうね?
ということで今回は前回の補足的にそのあたりの話を書きます。
(が、そこから話は意外な展開に…?)
~What does/is “harmonic” mean?~
「調和」というとピンと来ませんが、外来語で言うと(この文脈では)「ハーモニー」です。”Harmonic Mean” とはすなわち「ハーモニー的な平均」です。ハーモニーと言えば音楽。和音とかの世界です。
音は振動で伝わり、ドレミファソラシドなど音の高さは振動数 (一定時間で何回振動するか) で決まります。振動数が大きくなるほど、高い音になります。たとえば 440Hz (1秒で440回の振動) はラの音で、倍の 880Hz だと 1オクターブ上のラの音です (「ラの音は 442Hz のほうがいい」とかいう人はとりあえず今は黙ってて下さい:-)。
ギターのように弦を弾いて音を出すとき、弦の材質と太さ、そして引っ張る強さが同じであるならば、弦が長いほど振動数は小さくなり、短いほど大きくなります。弦の長さが半分だと、振動数は倍になります。
振動が伝わっていくとき、そこには波が生まれます。振動の伝わる速さと、一回の振動に掛かる時間で、一つの波の長さ (波長) が決まります。弦はそれ自体が振動することで音を出しますが、弦の上でも波が伝わります。下のようなかんたんな模式図で表されるように、弦の出す音の (弦の上での) 波長は、弦の長さの二倍になります。(細かく言うと弦の上には波長がその半分や1/3などの (その長さに切りよく収まる) 波もでき、それらの分の音の成分を倍音といいますが、ここでは気にしないでおきます)
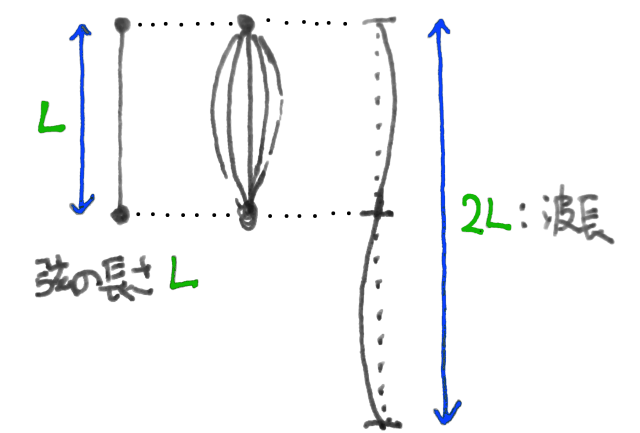
そうすると、弦の長さが半分になると波長も半分になります。振動数は倍になりますから、波長と振動数は反比例の関係にあることが判ります。振動数を f, 波長を L とすると、f×L = C (C は弦の材質・太さ、引っ張る強さで決まる定数) と表せます。
二つの音は、それぞれの波が切りの良いところで重なる、すなわち波の長さがかんたんな整数の比になっているときにきれいに響きます。1オクターブ違う音の波長の比は 2:1 で、これはオクターブ違いの「同じ音」として響きます。
オクターブを超えない、2倍以内の範囲での次にかんたんな比は 3:2 です。長いほうの波長二つぶんのところに、短いほうの波長三つぶんがちょうど収まります。長いほうの音を「ド」とすると、短いほうの音は (純正律という音階の決め方での)(その上の)「ソ」に当たります
(以下、特に断りのない場合は純正律での音階ということで話を進めます)。この「ド」と「ソ」はドミソという最も知られているであろう和音にも含まれるように、きれいに響く音の組み合わせの代表格です。
ドとソの波長の比は 3:2 なので、ドの波長を1とすると、ソの波長は 2/3 です。1オクターブ上のドの波長は 1/2 です。そして、1 と 1/2 の調和平均は、2/3 です。おお、(道のりが長かったですが^^;) ここについに調和平均とハーモニーの関係が!
f×L = C → L = C / f なので、弦の材質・太さや引っ張る強さが同じならば、「分子が同じ」ですね。
(ここで、「おや?」っと思う人がいるかも…)
f×L = C なので、C = 1 となるような f と L の単位 (あるいは設定) を持ってくると、f と L は互いに逆数となります。前回書いたたように
A と B の調和平均が M のとき、逆数をとった 1/A と 1/B の算術平均は 1/M になります。すなわち、ドと 1オクターブ上のドの波長の調和平均がソの波長になるのなら、逆数で考えると、ドと 1オクターブ上のドの周波数の算術平均がソの周波数になります。
算術平均と調和平均は裏返しの関係、というのが判りやすい例ですね。
既に気づいた方もいるかもしれませんが、「f×L = C → L = C / f なので…分子が同じ」というのなら、
f×L = C → f = C / L
でもあり、周波数で見ても「分子が同じ」です。こっちも、算術平均でなく調和平均を適用したほうが適切なのでは?
ちなみに、ドと 1オクターブ上のドの周波数の調和平均は、ファの音の周波数になります。波長で見ると、ドの波長の 3/4 がファの波長になるので、ファの波 4つでドの波 3つぶん、これもきれいに響きます。そしてもちろん、ドと 1オクターブ上のドの波長の算術平均は、ファの音の波長になります。
この場合はどちらをとっても意味がある、とはいえ何かもやもやします。よくよく考えれば前回挙げたオームの法則の例の場合も、R = V / I で V が一定 (「同じ」) ならば、I = V / R と書いても「分子の(V が)同じ」です。そして、二本の抵抗を並列につないだとき、それぞれの抵抗を流れる電流の平均は、算術平均で計算できます。
これらはどう考えれば…。
最終的には「個別の事例の (物理的な) 意味合いを考えて適切なほうを選ぶ」になってしまうのかもしれませんが、弦の長さと音の周波数、オームの法則の例などを考えると、反比例する二つの量のうち、どちらが直接調整できるもので、どちらがそれに連動して(自動的に)変化するものかを考え、直接調整できるものの平均を考えるときは調和平均が適切、ということになるかと思います。 「適切」とは、解りやすい意味を持つということと考えるとよいでしょう。
弦の長さを変えることで音の周波数は変わりますが、音の周波数を変えることで弦の長さを変えることは (少なくとも普通は) できません。抵抗を取り替えて流れる電流の量を調節することはできても、流す電流の量を変えて抵抗値を変えることも (普通は) できません。
他の例でもたとえば、ある距離を往復するのに往きとかえりで速度が違う場合、移動速度を変えることで掛かる時間は変わりますが、掛かる時間を設定してそれに合う速度を決めるのには計算が必要です。感度と適合度から計算する F値の場合も、検査の種類や有病率で感度や適合度が決まるのであり、その逆ではない、と考えればまあ合っているかと思います。
音の場合は「音の周波数を変えると、長さの違う弦や筒、金属の板のうち、共鳴するものが変わる」というようなことは可能です。そのあたりが周波数の調和平均にも意味が考えられる、ということにつながっているかもしれません。
挙げたもの以外の例でも本当にそうなのか? とか、なぜそうなのか? とかもやもやした部分はまだ残ります。理解が進んだら、また続編を書きたいと思います。




