こんにちはAITCのmasatoです
AI分野で最近注目され始めている技術をご存知でしょうか?
それがリザバー計算という技術です!
これは「時系列データを使った分類や予測が低コストで高速に学習できる」
素晴らしい技術です。
今回の記事では、リザバー計算という技術を
セルオートマトンというものを用いて実装してみようと思います!
お楽しみに!
リザバー計算とは何かを知らない方は
前回、「リザバー計算 理論編」を執筆しましたので
こちらの記事をご覧ください!
リザバー計算ではその名の通りリザバーというものを使って計算します
リザバーは容器に貯められた水、タコの足、量子系など
過去の情報をなんらかの形で現在に残すことができるものです
今回は、実際に論文でリザバー計算ができることが確認されている
セルオートマトンというものを用いてリザバー計算を実装してみたいと思います
その前にセルオートマトンとは何か理解していきましょう!
セルオートマトンとはなんだか難しそうだなあと思ったかもしれません
しかし、非常にシンプルなアルゴリズムでできているので安心してくださいね!
まずオートマトンについて説明しましょう
オートマトンはなんらかの入力によって内部状態が0または1に変化するもののことをいいます
イメージとしては次のようなものです!
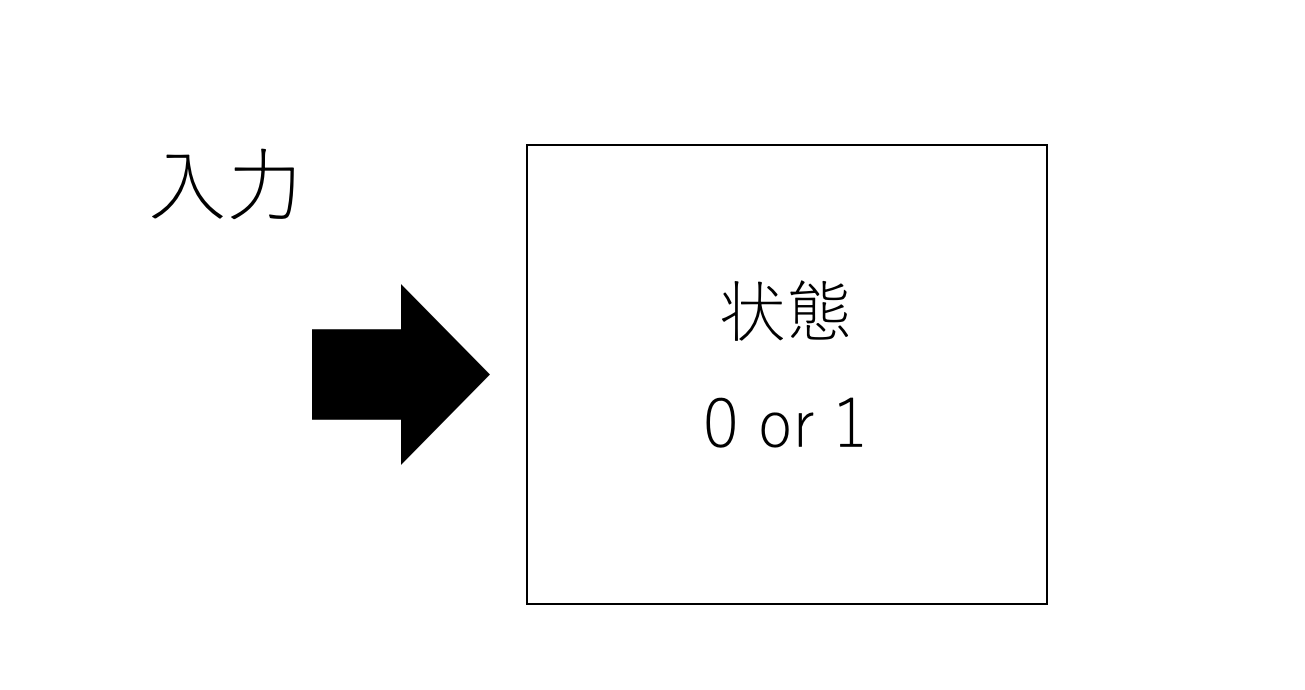
例えば自動販売機にお金を入れると
購入できないモードから、購入できるモードに変わりますよね
このようなモードの変化を内部状態だと思っていただいて構いません!
そしてセルオートマトンは何かというと
オートマトンをマス目に配置したもののことを言います
オートマトンを
横並びにしたものを一次元セルオートマトン
横と縦に並べたものを二次元セルオートマトンといいます
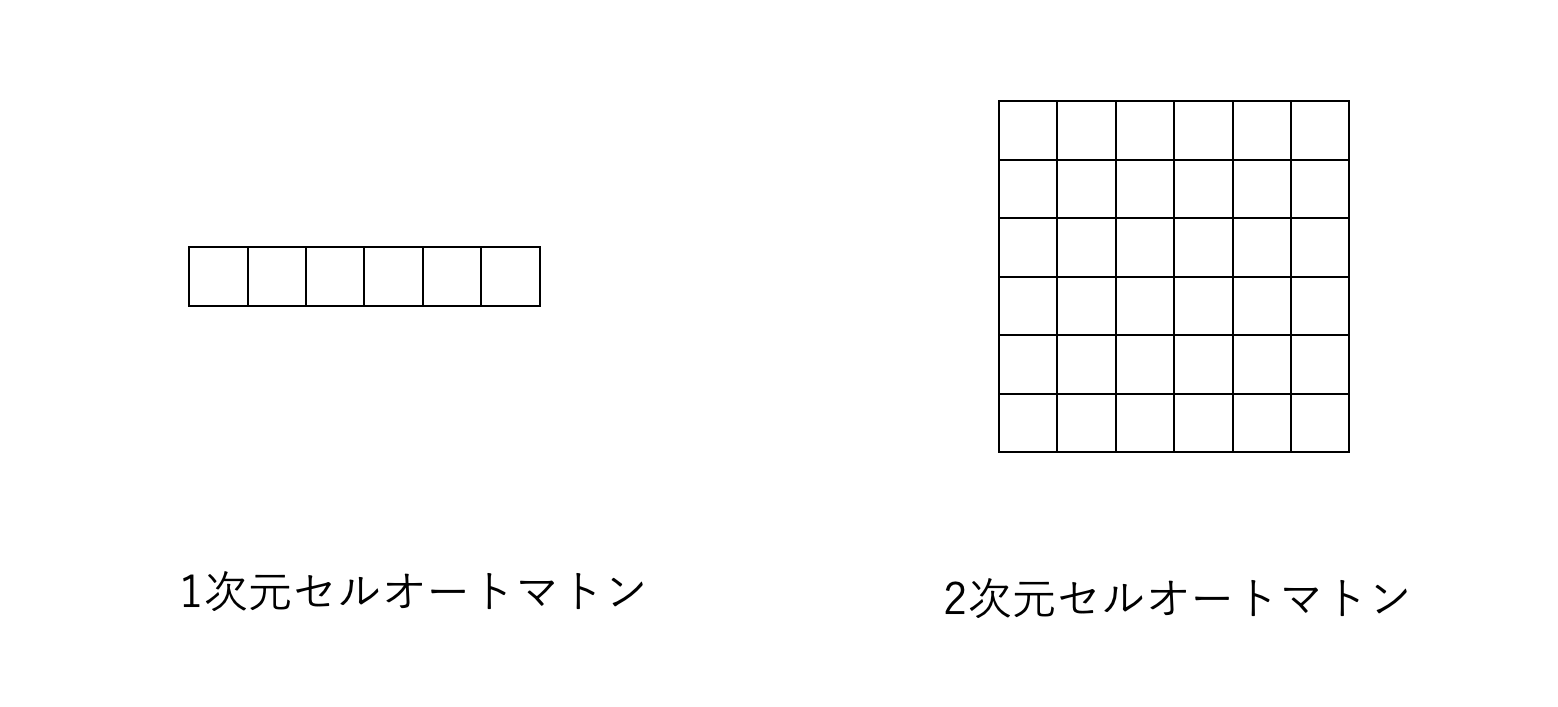
さてこの時、マス目に配置されたオートマトンをセルと呼ぶことにします
セルは、近くのセルの状態を入力にして内部状態を変化させます
マス目の配置の仕方や、
2マス隣までのセルの内部状態を入力とするか
それともただ隣のセルの内部状態を入力するかなどの違いで
様々なセルオートマトンが存在します
その中でも代表的な初等セルオートマトンについて説明しますね!
今回リザバー計算で用いるのも、この初等セルオートマトンです
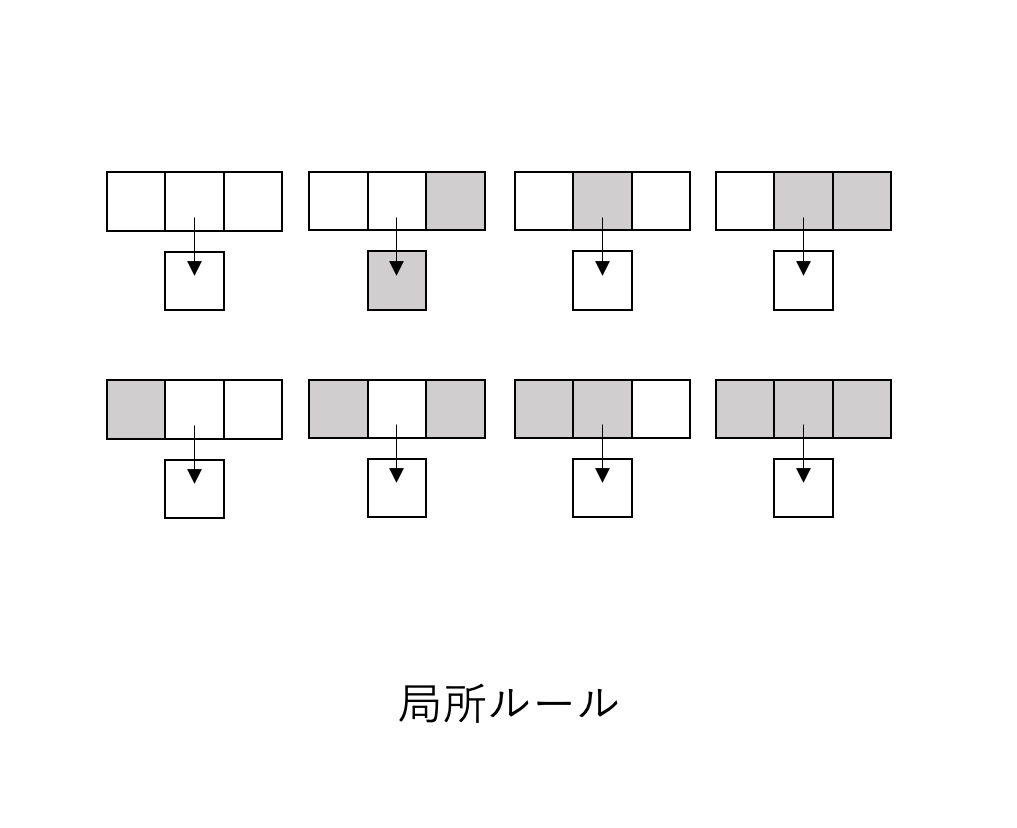
初等セルオートマトンでは両隣のセルの状態によって内部状態が変化します
そして、どのような状態でどう変化するかはあらかじめ決めておきます
例えば、オートマトンの両隣が0なら内部状態は0となり
左隣が0で右隣が1なら内部状態は1となるようにと決めておきます
これを局所ルールと呼びます
実際に内部状態が0の時は白色のセル、1の時は黒色のセルとして
局所ルールとして図に表してみると次のようになります
初等セルオートマトンは
この局所ルールにしたがって内部状態を変化していくだけです
とてもシンプルですよね
実際に、次のに4番目のセルの内部状態は1でそれ以外の場合は0の場合で
ルールを適用すると次のように変化していきます
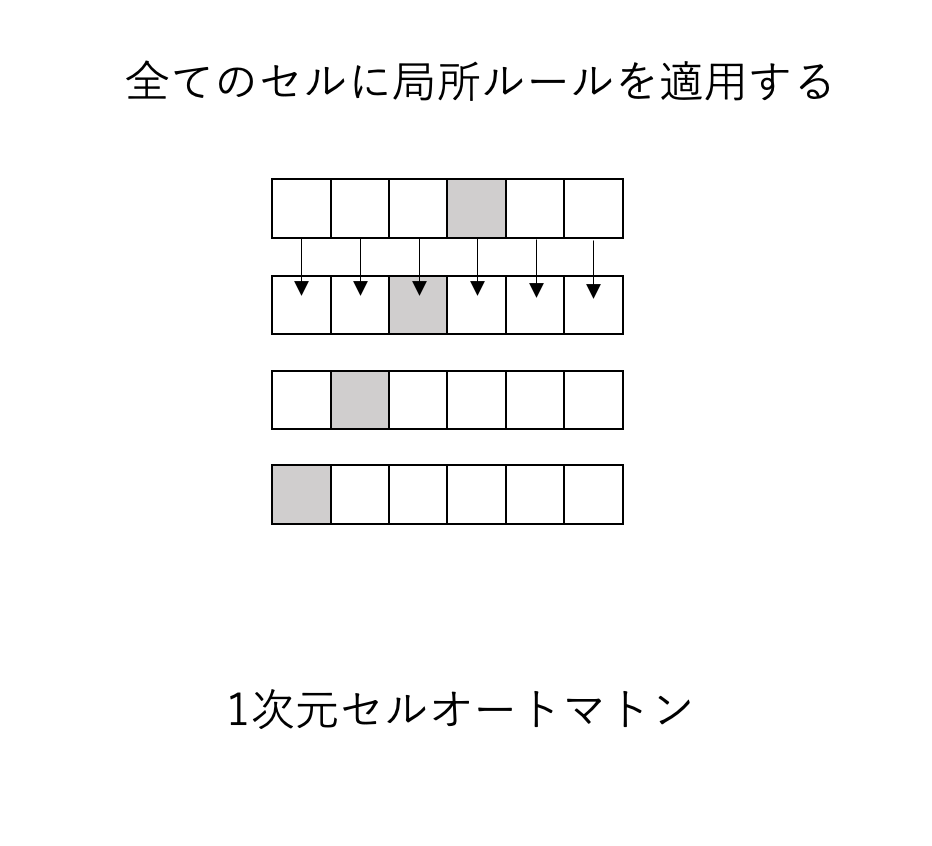
このように、時間ごとにオートマトンの内部状態によって白と黒で色付けして
並べると模様が浮かび上がりますよね
これを時空間パターンと呼びます
このパターンについてあとで詳しく説明するので覚えておいてください!
さて局所ルールの決め方は実は256個あります
なぜ、そうなるか説明すると
セルと両隣のセルの内部状態「0」と「1」の組み合わせは
「000」「001」「010」「011」「100」「101」「110」「110」
の8通りありますよね
ここで、その組み合わせを
a0・・・a7と言うふうに記号として表します
a0・・・a7
は0か1になるので2の8乗の組み合わせがあり
256通りのルールがあることがわかります
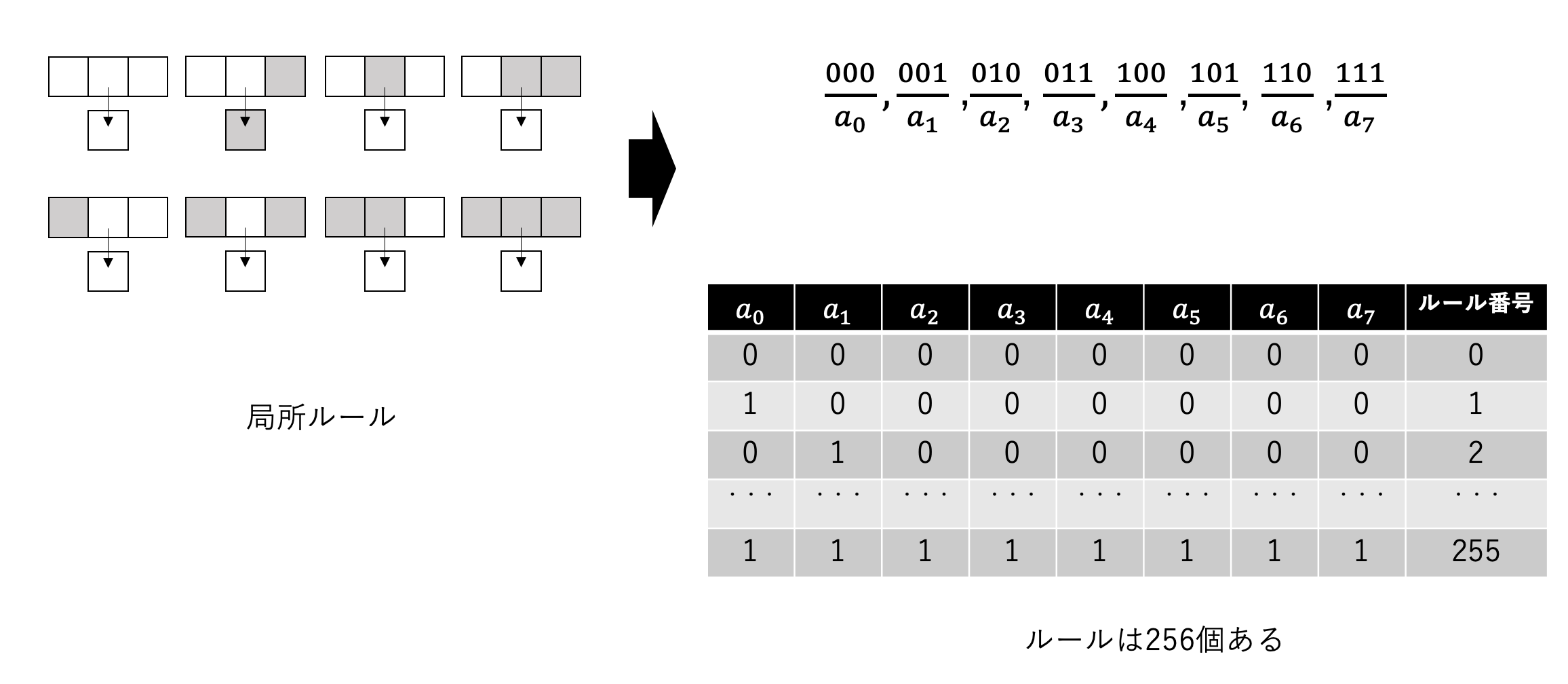
このように1次元セルオートマトンにはたくさんのルールがあるんです
このルールによっていろんな時空間パターンが見られるので見てみましょう!
こんなにシンプルな初等セルオートマトンですが
局所ルールの決め方で時空間パターンが大きく4クラスに分類できることが知られています!
以下のように、「一様」「周期的」「カオス」「複雑」があります
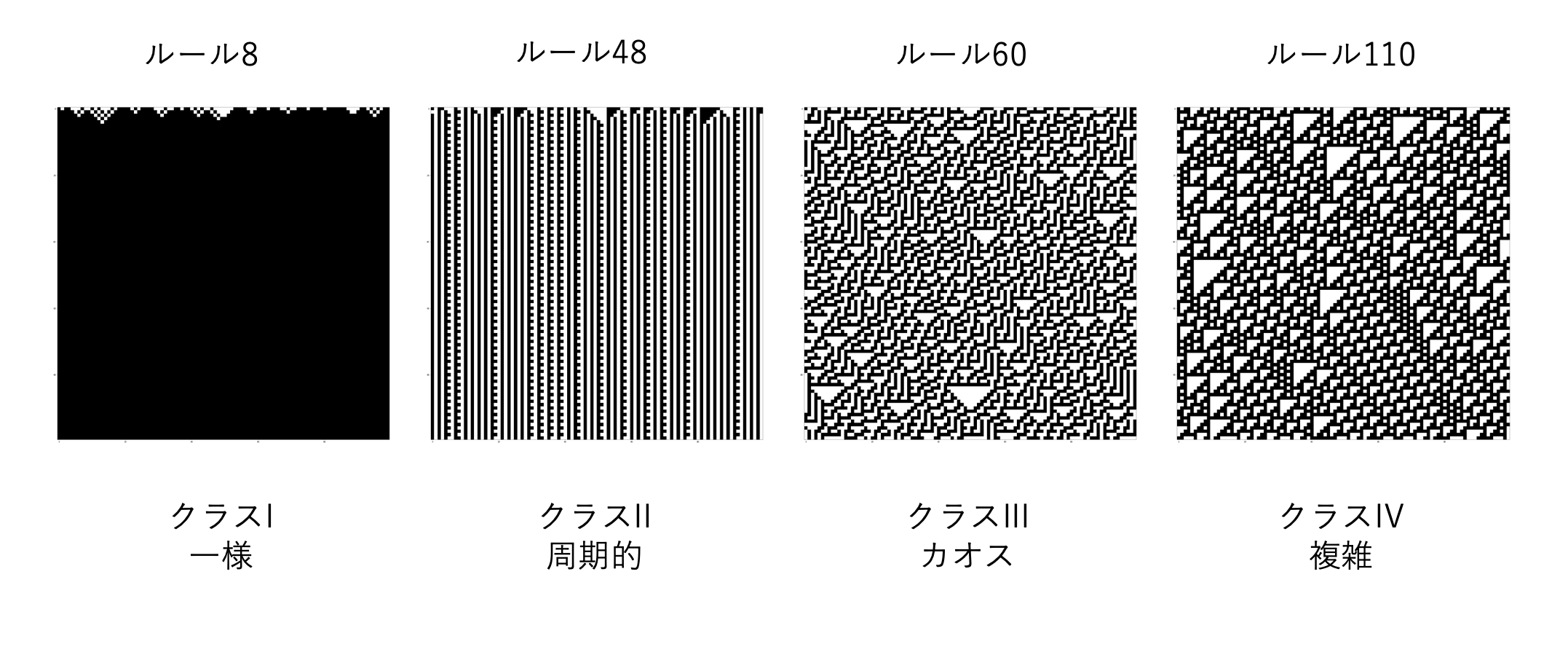
クラスIの「一様」では全てのオートマトンの内部状態が0か1になります
クラスIIの「周期的」ではオートマトンの内部状態の周期性を確認できます
クラスIIIの「カオス」では完全にランダムなパターンを繰り返していきます。ランダムなので予想することができません
そして重要なのがクラスIVの「複雑」です。
これは、周期性とランダム性を区別できないという意味で複雑なのです
このクラスでは、周期的なパターンをしたかと思えばランダムなパターンをみせるので
とても不思議です!
リザバー計算では
「カオス」と「複雑」クラスでリザバー計算で使えることが知られています
結論からいうと
クラスI~IIIよりクラスIVの「複雑」でリザバー計算の性能が一番良くなるといわれています
余談ですがこのクラスIVには計算万能性と言う性質がありまして
これを使うことでコンピュータを作ることが理論的に可能といわれています
とても面白いですよね!ここでは説明できませんが、気になる方は調べてみてください
個人的に、人工知能の発展のために非常に興味深いものだと思っています!
これでセルオートマトンの基本について理解できたと思います
ここでは、実際にセルオートマトンを使ってリザバー計算の実装方法について説明していきます
説明のために時系列入力を4ビット、出力を3ビットとすると
イメージとしては次のようにリザバー計算を実装していきます
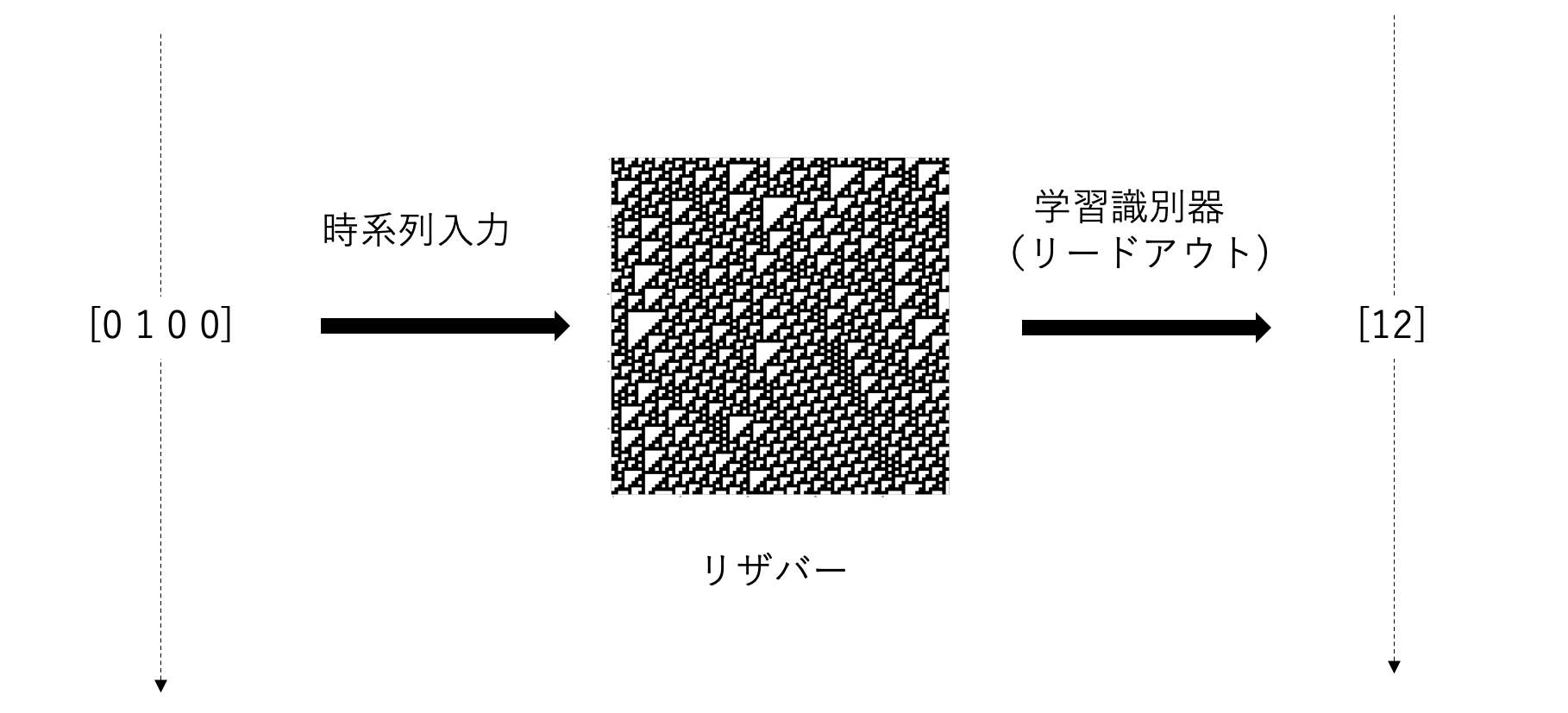
これはざっくりとしたセルオートマトンを用いたリザバー計算の流れのイメージです
これから、詳細に説明していきますが、まずは大まかに説明します
まず、リザバー計算では時系列入力を扱うので
t=0なら[0100]、t=1なら[1000]、t=2なら[0011]…
というふうに時間に紐付けたデータを用意して入力します
次に
データを入力するとリザバーはセルオートマトンを採用しているので
時空間パターンを生成します
最後に、時空間パターンをもとに線形学習器を用いて、分類や回帰を行ない出力します
このようにしてリザバー計算を行なっていくのです
ここまでは、大まかなイメージを掴んでいただければ大丈夫です
さてこれから、より詳細にリザバー計算の流れを
次の3つのステップに分けて説明していきます
- 入力値を初期状態として設定する
- 局所ルールによって時空間パターンを生成する
- 時空間パターンから線形学習器で分類や回帰を行う
一つずつ見ていきましょう
まずt=0で[1000]のデータを入力した場合を考えてみましょう
その時、ランダム結合という処理を行い初期状態を設定します
状態が0のセルをL個用意し以下のようにランダムに結合していきます
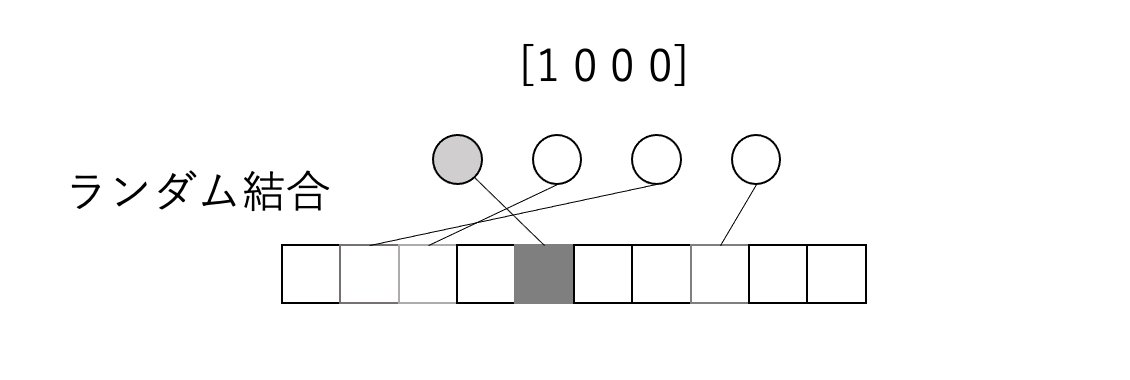
ここで同じ[1000]の入力でランダム結合したものをS個作ります
(ただし、ランダム結合の仕方は異なります!)
そして局所ルールをI回適用して時空間パターンを生成します
t=0のI回適用した時のセル空間に対して、
t=1の[0100]の入力とランダム結合を行います。これをリカレント結合と呼びます
これによって前の時間の情報を渡していると解釈できます
次の例では局所ルールを4回適用した例です
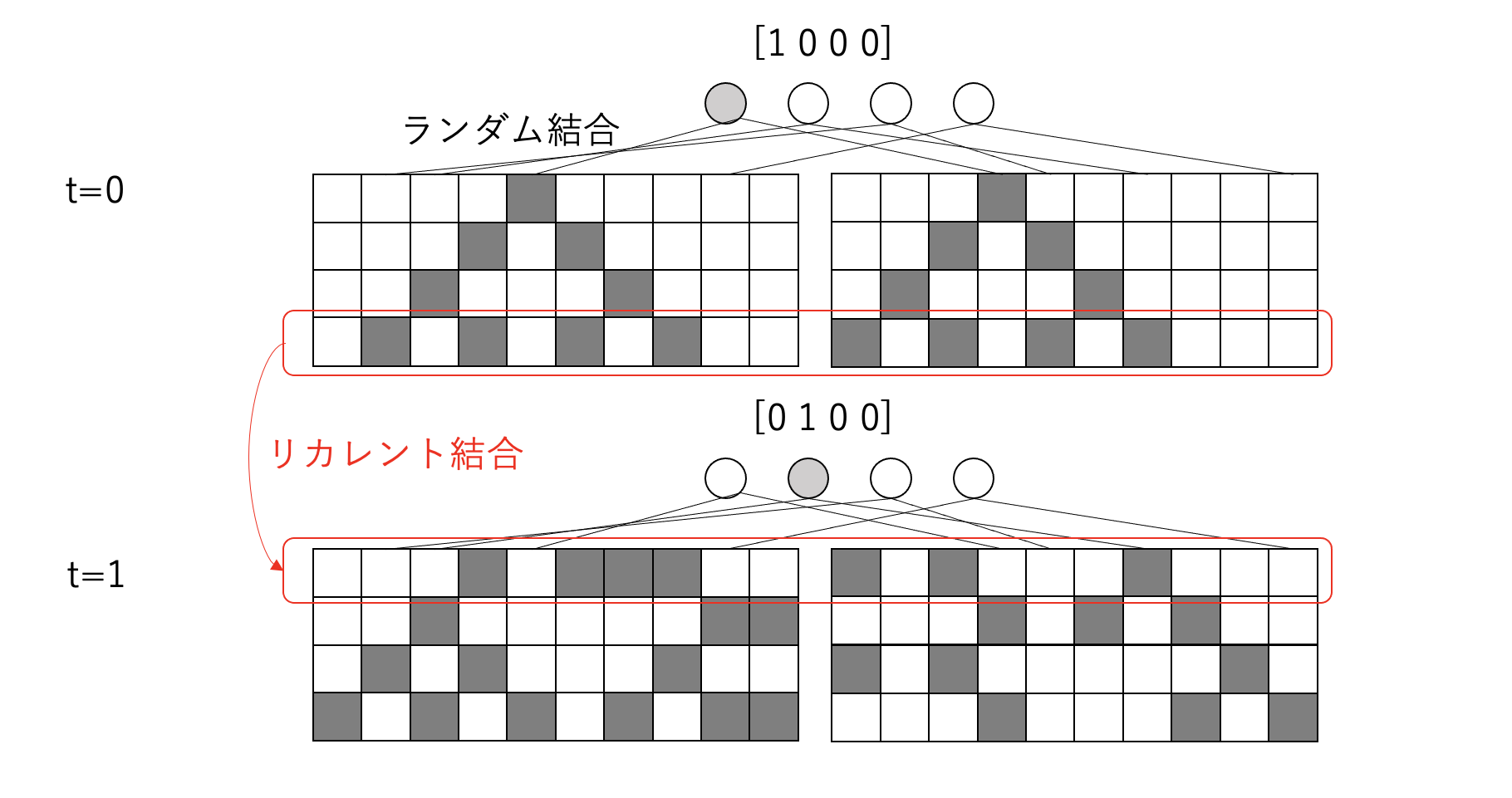
t=2, t=3,…も同様にして時空間パターンを生成します
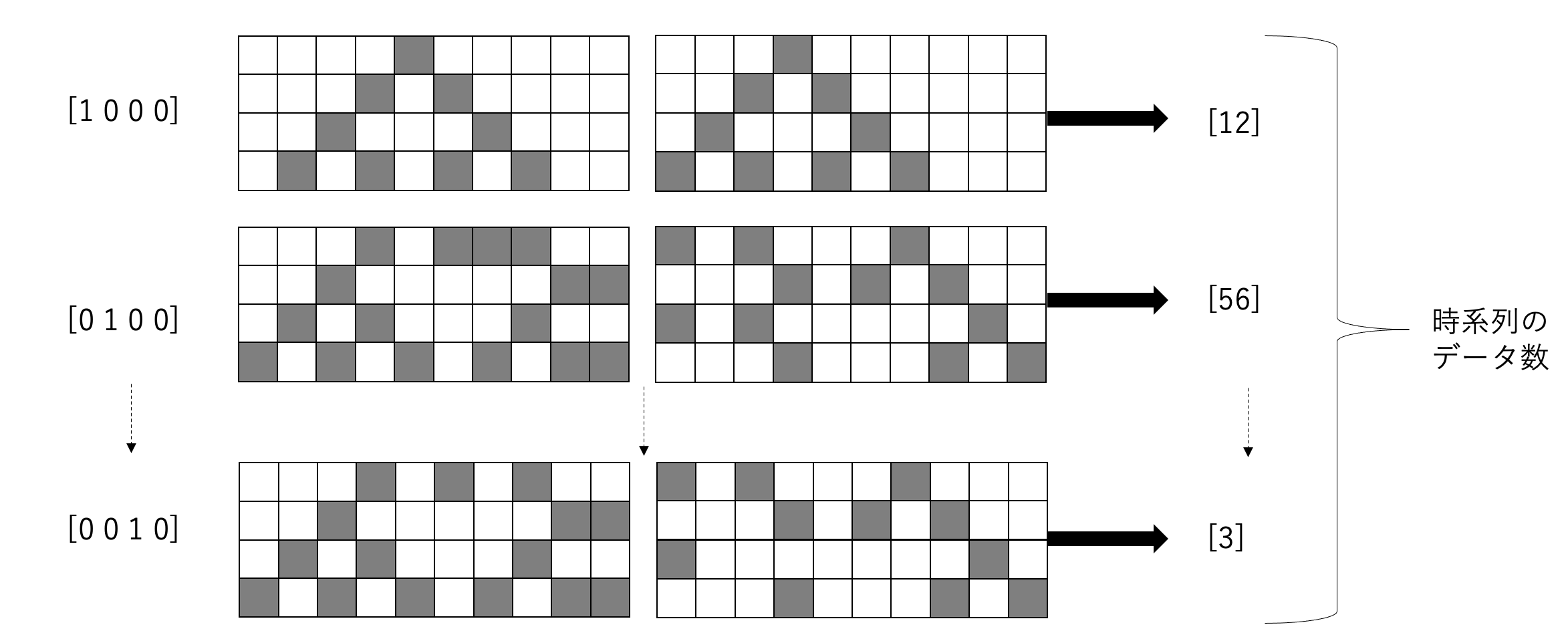
すると時系列のデータの数だけ時空間パターンができます
時間ごとに、時空間パターンをもとに線形学習器に分類や回帰をさせて値を出力させます
この例では、以下のように[1000]の時空間パターンから線形学習器に[12]を出力させています
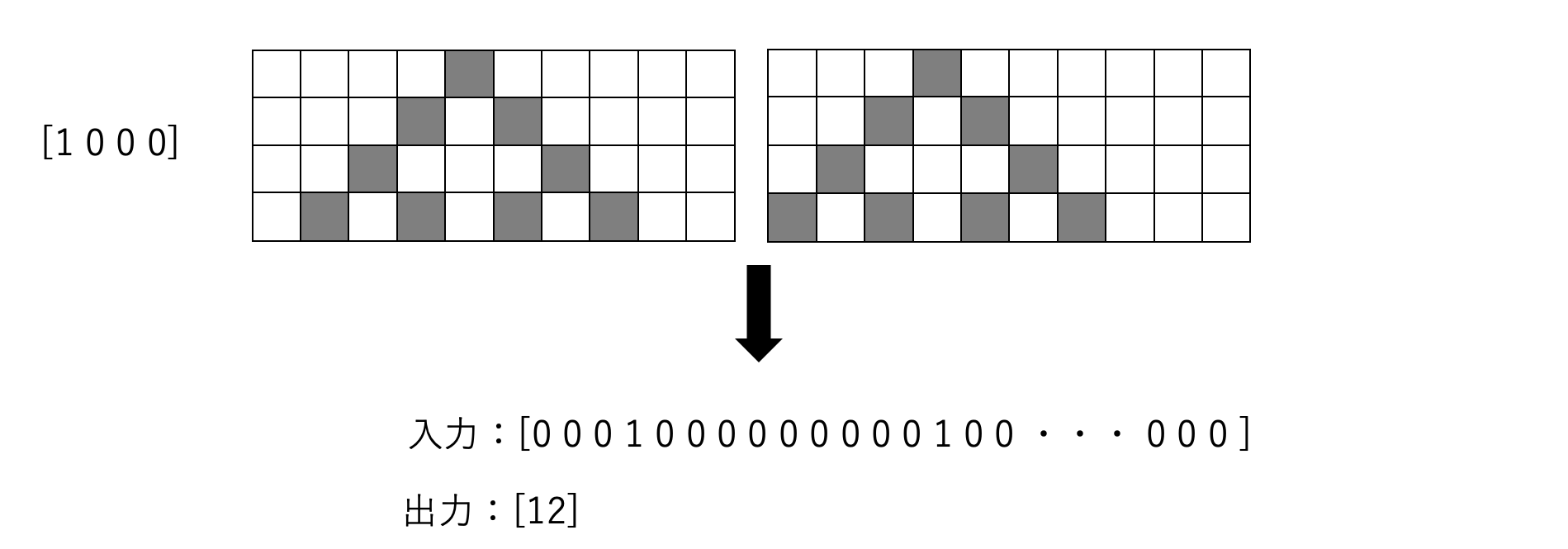
そして、補足として学習の方法ですが
t=0の入力データが[1000]と正解データ[12]を用意して
[1000]で生成される時空間パターンと正解データ[12]を線形学習器に渡して学習させます
時空間パターンは次のように
[0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 ・・・ 0 0 0 ]の高次元特徴ベクトルにして
線形学習器に入力し、正解データの[12]と照らし合わせて学習させます
さて以上のようにセルオートマトンのリザバー計算の方法について説明しました
最後にリザバー計算を使って入力した正弦波を生成してみます
今回セルオートマトンを用いたリザバー計算では2進数のものしか入力することができません
なので、正弦波を用意して時間ごとの値を2進数に変換して入力しています
学習時に使う正解データは2進数に変換する前の値を採用することにします
それでは正弦波のデータの生成から見ていきましょう
まずは、必要なモジュールをインポートします
| import struct |
| import numpy as np |
| import matplotlib.pyplot as plt |
次に学習に使用するデータを取得する関数のコードです
細かく説明はできませんが、Numpyを使って正弦波のデータを作成し
出力データYに格納し
2進数に変換してから入力データのXに格納しています
| def get_data(seed, n_data): |
| """ |
| 学習に使用するデータの取得 |
| """ |
| n_features = 64 # 入力 64 ビット |
| n_time_series = 120 # 時系列数 |
| np.random.seed(seed) # 乱数シードを設定 |
| period = 30 #周期 |
| # 正弦波をdataに格納 |
| x = np.empty((n_data, n_time_series), 'int64') |
| x[:] = np.array(range(n_time_series)) + np.random.randint(-4 * period, 4 * period, n_data).reshape(n_data, 1) |
| data = np.sin(2.0 * np.pi * x / period).astype('float64') |
| # dataの値を2進数に変換してXに格納 |
| X = np.zeros((n_data, n_time_series, n_features), dtype='int64') # Xを初期化 |
| for idx,element in enumerate(data): |
| for idx2,e in enumerate(element): |
| b = double_to_bin(e) |
| for i,e in enumerate(list(b)): |
| if i > 1: |
| X[idx][idx2][i-2] = int(e) |
| # dataをYに格納 |
| Y = data |
| return X, Y # X:時系列データの入力, Y:時系列データの出力 |
また、これが2進数に変換する関数です
| def double_to_bin(f): |
| """ |
| 2進数に変換 |
| """ |
| b = bin(int(hex(struct.unpack('>Q', struct.pack('>d', f))[0]), 16)) |
| bits = b[2:] |
| if len(bits) < 64: |
| b = b[0:2] + "0"*(64-len(bits)) + bits |
| return b |
さて、これらの関数を使って学習データを生成して
Xの中身とYの値をグラフとして出力してみましょう
| n_data = 1 # データ数 |
| test_x, test_t = get_data(7, n_data) # 学習データの生成 |
| fig, ax = plt.subplots(1,1,figsize=(10,3)) |
| ax.set_title("SineWave_Output") |
| ax.plot(test_t[0, :]) |
| print(test_x[0, :]) |
出力結果は以下のようになります!
[[1 0 1 ... 1 1 1]
[1 0 1 ... 0 0 1]
[1 0 1 ... 0 0 1]
...
[1 0 1 ... 0 1 1]
[1 0 1 ... 0 0 1]
[1 0 1 ... 0 1 1]]
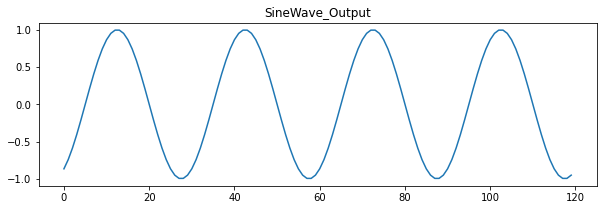
Xには120個の時系列データが入っています
一番最初の要素の[1 0 1 ... 1 1 1]がt=0の時の正弦波の値を2進数に変換したものです
2番目はt=1、3番目はt=2,…というふうに順番に格納されています
Yの正弦波出力はt=0から120まで、間隔を1としてプロットしたものです
これを用いてリザバー計算モデルを学習させていきます
次に、リザバー計算モデルを実装コードです
こちらも細かな説明は割愛させていただきますが
今まで説明してきたことをそのまま実装しています
ここでは大まかな構成を説明します
入力層とリザバー層とリードアウト層をそれぞれクラスとしてまとめ
それらを用いてリザバー計算モデルのクラスを実装しています
リザバー計算モデルのクラスでは
学習と予測の2つの関数を使えるように実装しています
また、リーアドアウト層では
線形学習器として、scilit-learnライブラリの線形回帰モデルを採用しています
このモデルで重回帰分析を行なっています
当然ですが
この線形回帰モデルはニューラルネットワークの回帰に比べてかなり高速に計算できます
リザバー計算では学習にこのような線形学習器を使うので
大幅に計算コストを削減することが可能になります!
| from sklearn.linear_model import LinearRegression |
| global input_vec_size |
| global size_multiple |
| global space_size |
| global random_mappings |
| global iteration |
| global ca_rule |
| global n_data |
| n_data = 100 # 学習データ数 |
| input_vec_size = 64 # 入力ベクトルのビット数 |
| size_multiple = 2 # 空間サイズを決定するパラメータ |
| space_size = size_multiple * input_vec_size # 空間サイズ |
| random_mappings = 6 # ランダム結合のマッピング数 |
| iteration = 4 # 局所ルールの適用回数 |
| ca_rule =110 # 局所ルール番号 |
| # 入力層 |
| class Input: |
| def __init__(self, W, X): |
| """ |
| 初期化関数 |
| """ |
| self.X = X |
| self.W = W |
| def __call__(self): |
| """ |
| ランダム結合を行う関数 |
| """ |
| n_data, n_time_series, n_features = self.X.shape |
| Y = np.zeros((n_data , n_time_series, self.W.shape[0]), dtype='int64') |
| for i in range(0, n_data): |
| Xt = self.X[i, :, :] |
| for t in range(0, n_time_series): |
| Y[i, t, :] = np.dot(self.W, Xt[t,:]) |
| return Y |
| # リザバー層 |
| class Reservoir: |
| def __init__(self, X, WI): |
| """ |
| 初期化関数 |
| """ |
| self.X = X |
| self.WI = WI |
| self.ca_rule = ca_rule |
| def __call__(self): |
| """ |
| 時空間パターンを出力する関数 |
| """ |
| n_data, n_time_series, n_features = self.X.shape |
| reservoir_size = space_size * random_mappings * iteration |
| Y = np.zeros((n_data, n_time_series, reservoir_size), dtype='int64') |
| for n in range(0, n_data): |
| for t in range(0, n_time_series): |
| if t==0: |
| RI = np.zeros(space_size * random_mappings) |
| R0 = self.X[n,t,:] + self.WI * RI |
| R = self.make_pattern(R0) |
| RI = R[iteration-1,:] |
| Y[n, t, :] = np.ndarray.flatten(R) |
| return Y |
| def make_pattern(self, x0): |
| """ |
| リザバーによって時空間パターンを作成する関数 |
| """ |
| # 初期状態の設定 |
| time_size = iteration |
| merge_space_size = space_size * random_mappings |
| cell = np.zeros((time_size, merge_space_size), dtype='int64') |
| cell[0,:] = x0 |
| # セル状態の時間発展 |
| for t in range(0, time_size-1): |
| for i in range(0, merge_space_size-1): |
| if i==0: |
| left=merge_space_size-1 |
| right=i+1 |
| elif i==(merge_space_size-1): |
| left=i-1 |
| right=0 |
| else: |
| left=i-1 |
| right=i+1 |
| # セル状態の更新 |
| s = 4*cell[t,left] + 2*cell[t,i] + cell[t,right] |
| cell[t+1,i] = (ca_rule >> s) & 1 |
| return cell |
| # リードアウト層 |
| class Readout: |
| def __init__(self): |
| """ |
| 初期化関数 |
| """ |
| self.model = LinearRegression() # 線形回帰モデル |
| def fit(self, X, t): |
| """ |
| 線形回帰モデルに学習させる関数 |
| """ |
| # 学習フェーズ |
| x = np.reshape(X, (np.size(X, 0) * np.size(X, 1), np.size(X, 2))) |
| t = t.reshape(-1) |
| X_train = x[:] |
| T_train = t[:] |
| # モデルの学習 |
| self.model.fit(X_train, T_train) |
| def predict(self, X): |
| """ |
| 線形回帰モデルに予測させる関数 |
| """ |
| X = np.reshape(X, (np.size(X, 0) * np.size(X, 1), np.size(X, 2))) |
| predict_y = self.model.predict(X) |
| return predict_y |
| # リザバー計算モデル |
| class ReservoirComputing: |
| def __init__(self): |
| """ |
| 初期化関数 |
| """ |
| self.W, self.WI = self.__set_W_WI() |
| self.Readout = Readout() |
| def fit(self,X,t): |
| """ |
| 訓練用データに適合させる関数 |
| """ |
| # 入力層 |
| input_layer = Input(self.W, X) |
| y = input_layer() |
| #リザバー層 |
| reservoir_layer = Reservoir(y, self.WI) |
| y = reservoir_layer() |
| self.Readout.fit(y, t) |
| def predict(self, X): |
| """ |
| 入力データから出力データを予測する関数 |
| """ |
| # 入力層 |
| input_layer = Input(self.W, X) |
| y = input_layer() |
| #リザバー層 |
| reservoir_layer = Reservoir(y, self.WI) |
| y = reservoir_layer() |
| y = self.Readout.predict(y) |
| return y |
| def __set_W_WI(self): |
| """ |
| 入力の重み W 、リカレント結合の重み WI の決定 |
| """ |
| W = np.empty((0, input_vec_size), int) |
| for i in range(random_mappings): |
| W0 = np.r_[np.eye(input_vec_size), np.zeros([space_size-input_vec_size,input_vec_size])] |
| W0 = np.random.permutation(W0) |
| W = np.append(W, W0, axis=0) |
| WI = np.mod(np.sum(W,1)+1, 2) |
| return W, WI |
次に作成したリザバー計算モデルを学習させてみます
| def run(): |
| """ |
| リザバー計算モデルを学習させる関数 |
| """ |
| train_x, train_t = get_data(2, n_data) # 訓練データの生成 |
| ReservoirComputer.fit(train_x, train_t) |
| ReservoirComputer = ReservoirComputing() |
| run() |
最後にテスト用のデータを作成して
リザバー計算に予測させた結果を見てみましょう!
| def output(): |
| """ |
| リザバー計算モデルに |
| 入力データから出力データを予測させる関数 |
| """ |
| test_x, test_t = get_data(7, n_data) # テストデータの生成 |
| test_x = test_x[0:1,:,:] |
| predict_y = ReservoirComputer.predict(test_x) |
| fig, ax = plt.subplots(1,1,figsize=(10,3)) |
| ax.set_title("ReservoirComputing_Output") |
| ax.plot(test_t[0, :]) |
| ax.plot(predict_y) |
| output() |
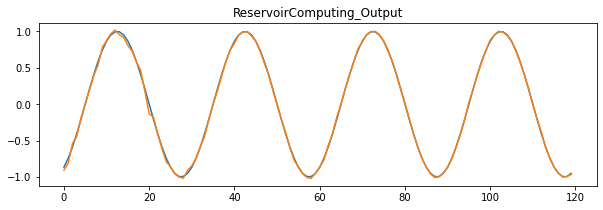
出力したグラフは次のようになりました
オレンジ線がリザバー計算の正弦波の出力結果で
青線が正解の正弦波のグラフです
(オレンジ線と青線は重なってしまっていて青線はほとんど見えてません)
比べてみるとかなり良い精度で正弦波を出力しています
t=0からt=20のあたりでガタガタしているのは
おそらく、セルオートマトンで生成される時空間パターンが
まだあまり特徴的でないため
線形学習器が正解の値とパターンを一致させることが難しいからだと考えられます
今回はリザバー計算の実装について説明しました
ニューラルネットワークを実装してみた方はわかると思いますが
ニューラルネットワークよりは非常に簡単に実装することができます!
RNNなどと比較してみたり
別のタスクに適用してみるのも面白い試みだと思いますので
ぜひチャレンジしてみてください!




