この記事は『CRESCO Advent Calendar 2022』の6日目の記事です。
みなさんこんにちは。データテクノロジーセンターの飯村北海です。
相変わらず、[PR]Tableauなどを活用したBI導入サービスを提供しています。
[PR]Tableauスタートパッケージのページができたので見てください。
昨年は縦持ち、横持ちに関する記事をデータとTableauで説明してみたのですが、今年もTableauに関する記事を書きたいと思います。
今回のテーマは歩数になりますので、その経緯などを先に書いてから、可視化の話に行きたいと思います。前置きを飛ばしてTableauでスパイラルチャート(Spiral Chart)の可視化の方法について知りたい方はこちらからご覧ください。
クレスコでは健康経営を掲げ、スポーツ庁「FUN+WALK PROJECT」への参画のプレスリリースにもあるように、その一環で社内でウォーキングイベントが実施されています。
2022年度に開催された社内ウォーキングイベントは下記です。
| 時期 | 開始 | 終了 | 日数 | 参加人数 | 私の成果 |
| 上期 | 2022年5月1日 | 2022年6月5日 | 36 | 200名超 | 約42万歩 |
| 下期 | 2022年11月1日 | 2022年12月4日 | 34 | 上記以上 | 計測中・・ |
下期のイベントが始まる前に、とある役員の方が、全社員が加入しているTeams「ヨクスル」※上に「『社員の歩数で地球をn周するぞ!』という目標を掲げるのはどうか?」という提案があり、Tableauで歩数を可視化するのは面白そうだなと思った次第です。
※第1位に「ヨクスル」のトピックが説明されています。ご参照ください。
厚生労働省が出している身体活動・運動|厚生労働省 (mhlw.go.jp)のページでは、
1,000歩は約10分の歩行で得られる歩数であり、距離としては600?700mに相当する。
と記載しており、1歩当たり60~70cmということのようです。
オムロンヘルスケア社の歩幅の目安が知りたい | よくあるご質問 | オムロン ヘルスケア (omron.co.jp)のページでは、
歩幅の目安は「身長×0.45」です。
と記載しています。じゃぁ身長ってどれくらい?と思いますよね。
2018年のデータで20歳以上の男女の平均でみると、5211名分の平均身長が160.7cmになりました。
160.7*0.45=72.315≒72cmということで厚生労働省の方と比較すると1歩当たりやや長めになっているようですね。この記事の段落では計算を楽にするために、1歩は70cmとしておきます。また、地球1周の距離も4万kmとしておくことにします。
地球1周をするには40億センチメートル必要なので、40億÷70=57,142,857なので、約5千7百万歩必要、ということになります。
200名参加だとすると1人当たりの担当歩数は28万6千歩くらいです。上期の開催期間が36日なので、1日あたり8000歩を達成すれば1周はできそうです。
偶然にも一日の推奨歩数の8000歩と同じくらいになりましたね。みんなで地球1周しよう、という目標は到底無理というものでもなさそうです。
さて、勝手に考える要件としては地球を何周かしたときにそれを表現できるチャートを作ることができればよさそうです。円グラフとかそれに準ずるようなものをイメージして、Tableauで表現できるチャートはないか探してみることにしました。
いくつか探してみたところ、当初はRadial Chart(ラジアルチャート:放射状のグラフ)というチャートがよさそうな気がしていました。Radial Chartにも2種類ありそうで、棒円弧グラフ(造語です)の形式になっているものや、棒グラフのx軸の開始と終了をつなげて丸くしたものなどがあります。採用したかったのは棒円弧グラフでした。
また、Radial Chartと似たようなチャートにSun Burst Chart(サンバーストチャート)というのがありますが、Sun Burst ChartはPie Chart(円グラフ)に近いもので、Sun Burst Chartは階層型円グラフと説明できそうです。
Radial Chartは1周が360°とみなしたときに、基準ディメンションのKPIを100%としたときにその他のディメンションがどのくらい割合なのか?を表現するときに使われるようで、時計の針が12を指した真上の0%から初めて9時のところまで(270°分)を100%として表示することが多いようです。
いくつかTableau Publicで掲載されているワークブックを確認してみたのですが、基準角度270°を指定していて、360°を指定することもできそうなのですが、今回は純粋に地球を何周できるか?みたいな見せ方をしたいので、270~360°で終わってしまったり、360°を超えて表示するのには適していないということが分かりました。このブログをRadial Chartで書こうとしたのに、これでは〆切に間に合いません!
似たようなチャートがないかほかにも探したところ、Spiral Chart(スパイラルチャート)と呼ばれるチャートを見つけることができました(リンク先は英語です)。このチャートは文字通りらせん状に広がっていく形をとっており、アルキメデスの螺旋の極方程式をグラフで表現したようなチャートになっています。こちらであれば1周だけではなく、何周しても表現することができそうです!ということでこちらのタイプで作ってみましょう。
ちなみに、Tableauで標準で提供されている機能でチャートを作る場合、代表的なものは数表、棒グラフ、折れ線グラフ、面(エリア)グラフ、散布図、マップ(地図)、とありますが、ここで採用しようとしたRadial ChartとSpiral Chartはいずれも散布図で工夫するタイプの表現方法になっています。x座標とy座標のフィールドが必要(なければ計算)です。
Tableauで可視化するために必要なデータの構造を検討しましょう。任意の期間に集計した、複数の社員の歩数の合計が何kmになるのか?を表現したいので、日付、社員名(もしくは識別できるID)、歩数は最低限必要な列になります。後の分析で部門対抗などもできそうな気がするので部門も加えておきます。下記のようなイメージでしょうか(中のデータはサンプルです)。
| 日付(yyyy/mm/dd) | 社員名 | 部門名 | 歩数 |
| 2022/11/01 | 田中太郎 | 開発部 | 8,023 |
| 2022/11/01 | 鈴木次郎 | 総務人事部 | 12,011 |
| 2022/11/02 | 田中太郎 | 開発部 | 6,157 |
| 2022/11/02 | 鈴木次郎 | 総務人事部 | 10,983 |
| ・・・ | |||
※ここでは2名しかいませんが、仮のデータだということでご了承ください。
歩数から距離を出すのはTableau Dekstop側で出すか、Tableau Prep側で出すか議論はあると思います。
この記事での解説は割愛しますが、身長と係数のパラメータをTableau Prepで作成し、160cmx0.45で算出し、距離に置き換えています。
さて、データもそろいましたので、実際に作っていきます。必要な項目は散布図で表示するので、x座標とy座標、それを算出するための角度が最低限必要になります。前述の参考Webサイトでは、スパイラルな曲線をプロットするときにそのままだと原点(0, 0)から始まるので、inner(内径)とparameter(線同士の間隔)も調整変数としてパラメータで作成しています。この記事ではparameterだとTableauのパラメータと混同する可能性があるので、以降はspace(間隔)と呼ぶことにします。
座標にプロットする際の1つ1つの点を算出するロジックを説明していきます。
詳しくは「アルキメデスの螺旋 極方程式 極座標 代数螺旋」などのキーワードで調べていただければと思いますが、アルキメデスの螺旋を作るやり方になります。
r = a θ
x = r cos θ
y = r sin θ
上記のθの部分が「角度」、aは定数なので、いったん無視です。「x座標」、「y座標」は上記の式を計算して計算フィールドで作ります。
※社員の1日の歩数(距離)のデータ1件単位で点を打っていきます。
まず、角度についてですが割合で出したいので、360°の分母は地球1周の4万kmになります。分子は社員の歩数データ1件の距離になります。つまり「社員1人の1日の距離 / 地球1周の4万km」が角度となります。もちろん距離の合計が1周を超えてしまうと(100%を超えてしまう)、次の周になりますが、螺旋上に作成されるので、重なることはありません。また、0から社員の距離を出すと同じような場所に集まってしまうため、各データ(各社員)の距離(角度)を累計させています。
Tableau等で座標を出すためにはよく使われる弧度法で算出しており、1周360°を2πとしています。なので、角度を累計した距離を分子、地球1周の距離40万kmを分母とした割合に2πをかけたものを角度になります。
※度数法から弧度法への変換は度数 * π/180というのがありますが、度数/360 * 2πとも言えるので、後者で計算していることになります。
参考Webサイトでは1年365日が分母のうち、その日がどこに当たるか?という計算の仕方をしているのでn日目が分子、365日を分母で計算しているようですね。
次はx座標とy座標です。Tableauで標準提供されているSIN関数とCOS関数を利用できます。
角度からxとyの座標を計算できるので、cos(θ)がx、sin(θ)がyの値になり、そこにスパイラル要素を調整するため、inner(内径)で中心からの距離の調整、space(間隔)で線と線の間隔を指定しています。
内径の分だけ定数として原点からの距離が広がるようになっています。
また、歩いた距離の分だけ少しずつ広がるようになっています。
時計の針の12時の位置(上)から時計回りに進めるようにするために通常はx = r cos θで算出しますが、x = r sin θとy = r cos θで計算しています。
考え方はご理解いただけたと思いますので、具体的に計算フィールドを作成していきます。やっていることが分かりやすいように複数計算フィールドを作っています。
まずは角度、x、yを出すために必要なパラメータです。
こちらは今回、地球の1周を4万キロとしたので、整数型、400,000で作成します。
後で調整するので、整数型で1などとしておきます。
こちらも後で調整するので、整数型で1などとしておきます。
次に、前提となる計算フィールドです。
| RUNNING_SUM( SUM([距離_km]) ) |
RUNNNING_SUM関数は表計算関数の1種で、上記最初の距離から累計していくために使用しています。SUMがあるのは関数が集計または定数を引数に取る必要があるためです(ディメンション単位で集計するイメージをしてもらうとよいと思います)。
パーティション内の最初の行から現在の行までの、指定された式の累積最小値を返します。
| [内径] + ([累積距離_km] / [間隔]) |
ようやく角度、x、yです。
PI関数は数値定数πを返す数値関数です。
| ([n週目の累積距離_km] / [1周の距離_km]) * 2 * PI() |
| [半径r] * SIN([角度_θ]) |
| [半径r] * COS([角度_θ]) |
それぞれの点を打っていけば螺旋が作られるので、座標データであるxyをそれぞれ列シェルフ:x、行シェルフ:yに配置するだけで基本的にはできます。
今回は内径80、間隔3000に調整するとちょうどよいグラフになっています。
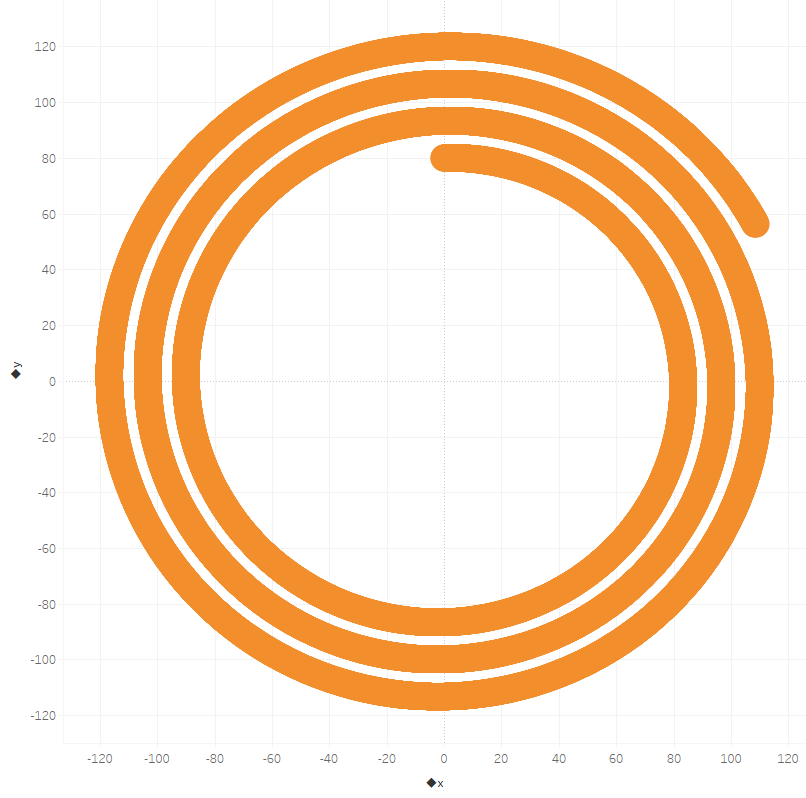
あとはダッシュボードにやりたいように組込みましょう
こんな感じで出来上がりました。いつものようにTableau Publicに保存しています。
ちなみにこちらの表現方法(スパイラルチャート)は今回のようなケースでは効果的かもしれませんが、実業務では、学習コストや使いやすさ(比較対象と比較しずらい)などの点で難しいため、他のチャートの利用を推奨していることだけ注意点として記載しておきます(実業務では掲示ダッシュボード上部のブレットチャートで事足りてしまいます…)。

歩いて何周できるか?ということをTableauで実現するために、結構いろいろと調べることになってしまいました。
特に弧度法や極方程式等について、Tableauで使用するためにわざわざ調べたことはなかったのですが、今回改めて調べる機会が得られたのはよかったと思います。
そして、このチャートはただ、歩数を合計して距離を出して可視化しただけなので、タイトルの旅行の要素がほとんどない状態ですよね?
はい。不完全燃焼な状態でもう1つやりたいことがあったもののできていないので、もう1記事、書くことにしようと思います。ということで次回(明日!?)に続きます!





