技研の (あ) です。
最近すっかり医療系の話に関わることが多くなってます。疾患の有無の判定などを行う際の性能指標について、これまで「感度とか特異度とか」「F値と平均的でない平均の話 〜あるいは調和平均の使いどころ」といった記事を書きました。
今回はその続きで、ROC曲線 (ROC Curve) と AUC について説明したいと思います。ROC曲線の話に行く前に、まずは判定の結果出てくる値に関しての話からです。
ニューラルネットワークなどを用いて疾患の有無を判定しようとする場合、たとえば、
- 「疾患なし」のもののデータを入力すると出力が 0、
- 「疾患あり」のもののデータを入力すると出力が 1、
になるように学習させます。
そして実際に判定したいものを入力したときに、それが「疾患あり」だったら出力が 1、「なし」だったら 0 とすべてきっちり分かれてくれればよいのですが、世の中そううまくはいきません。
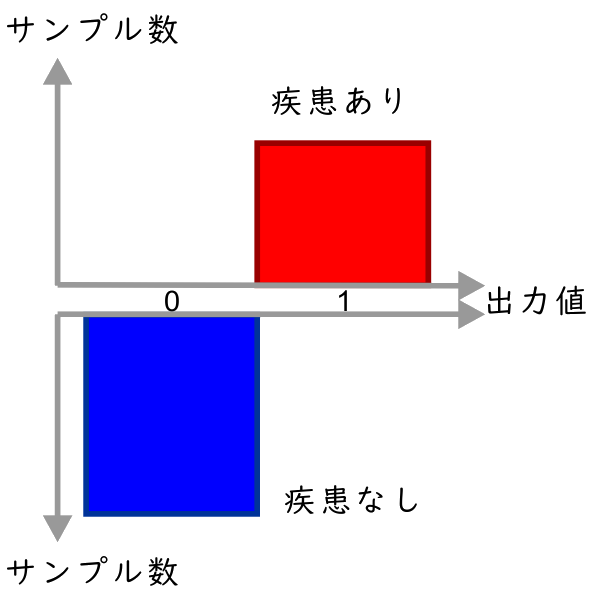
実際には、判定させてみると出力が 0.1 だったり 0.7 だったり 0.45 だったり 0.66 だったり…という感じになります。それでも、次の図 のように「疾患あり/なし」がどこかの値 (閾値, threshold) でスパッと区切れるのであれば万々歳です。その場合は感度も特異度も 100% の完璧な判定ができます。そしてもちろん、そんなにうまくいくことは (実際的な課題に対しては) ほとんど望めません。
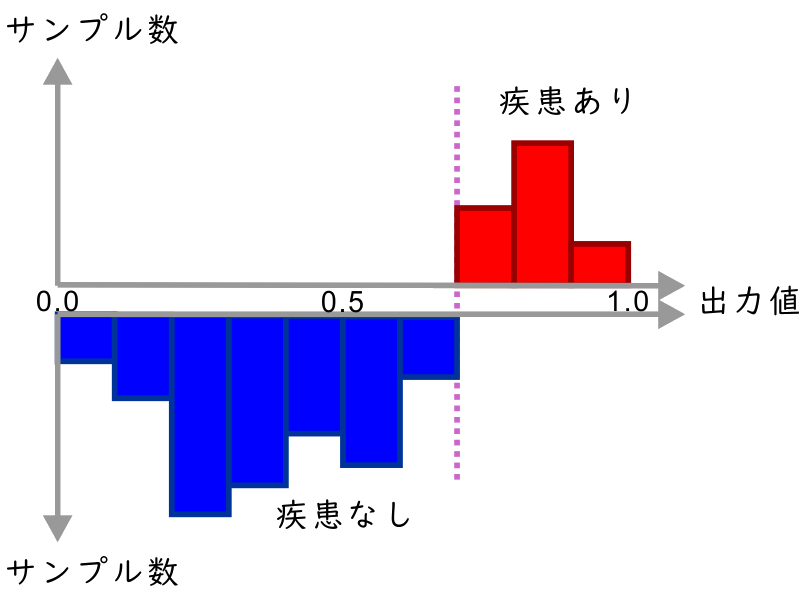
そんな状況の中で「(多少なりとも) 使える」判定とは、「『疾患あり』のものを分類したときの出力の分布と、『疾患なし』のものを分類したときの出力の分布を較べると差がある」もの、ということになります。つまり、ある閾値を決めて、それより出力が大きいもの (「陽性」として扱う) は、全体と較べて「疾患あり」のものの割合が多くなり、小さいもの (「陰性」として扱う) は
「疾患あり」のものの割合が少なくなる、というグループに分けられるもの、ということです。閾値をどう決めて分けても「疾患あり/なし」の割合が変わらない場合は「判定」として機能しません。
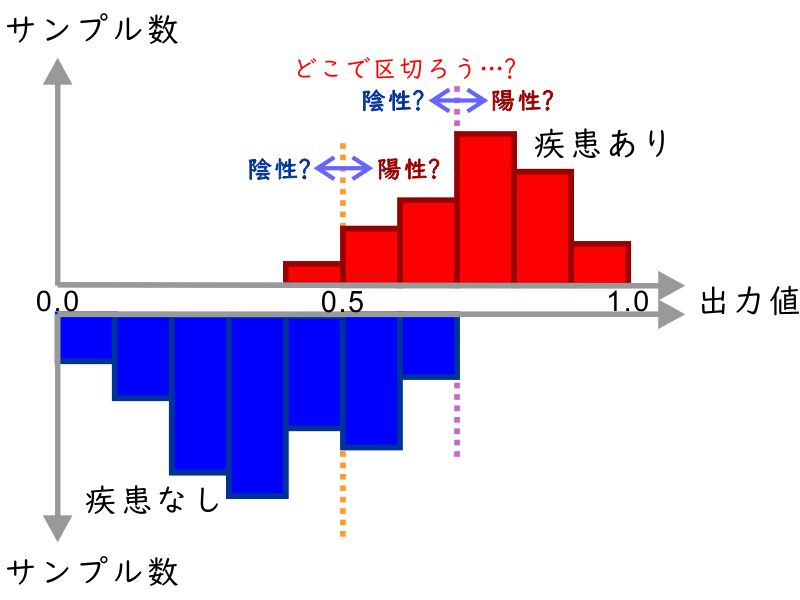
なかなかよい判定の場合、たとえば出力値の分布は上の図のようになります。「疾患あり/なし」の分布が重なる部分はありますが、重なる部分のどこかを閾値とすれば、「あり」が多いグループ (陽性) と「なし」が多いグループ (陰性) に分けられます。「あり」が多いグループに入ってしまった「なし」のものが「偽陽性」で、「なし」が多いグループに入ってしまった「あり」のものが「偽陰性」ということになります。感度 (疾患ありを見逃さない割合) を上げたければ閾値を低く、適合度 (陽性適中率、「陽性」のうち本当に疾患ありである割合) を上げたければ閾値を高くすればよいことが解ります。
使えなくはないけれどいまいちな判定の場合は、たとえば次の図のようにこの重なり部分が大きくなります。どこで切っても、「疾患あり/なし」の割合が少しはましになるとはいえ、感度も適合度もあまり上がりません。
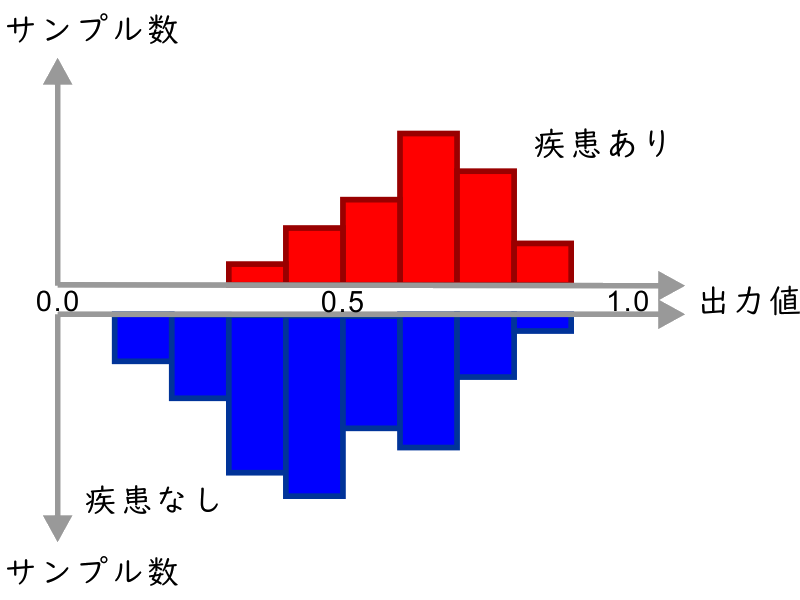
判定の良し悪しを見るために「閾値を変えたときにどれくらい切り分けられかたが変わるか」をグラフに表したのが、ROC曲線です。
ROC曲線の ROC とは Receiver Operating Characteristic の頭文字です。日本語だと「受信者動作特性」などと訳されます。元々はレーダーの研究からきた用語だそうで、それで「受信者 (receiver)」という言葉が出てきます。なるべくたくさん物体を検出できるように感度は上げたいけれど、そのときにどれだけノイズを拾うか、というところでしょうか。前節で書いた判定の場合と同じですね。
ROC曲線は、縦軸に感度、横軸に偽陽性率 (False Positive Rate) (1.0 – 特異度) を取ったときのグラフとして描かれます。縦軸も横軸ももちろん範囲は 0.0〜1.0 です。この上に、いろいろな閾値に対応する点を打っていきます。
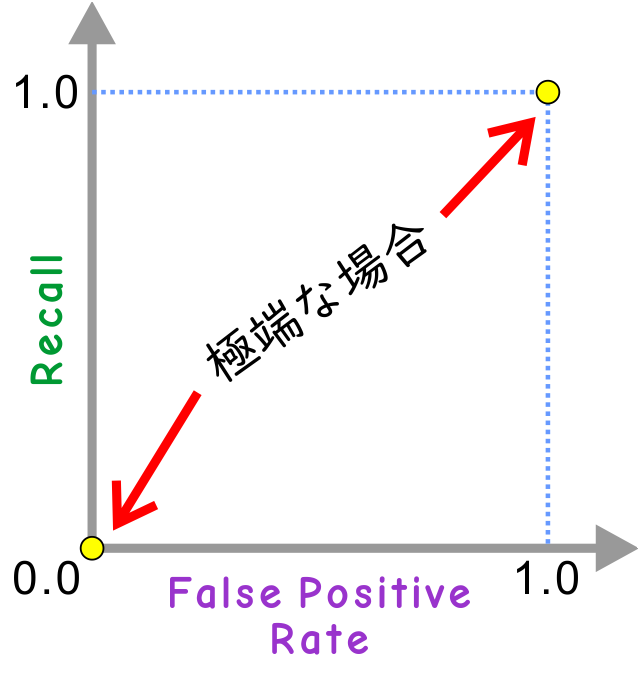
まず極端な場合から始めると、閾値を1.0 (というか +∞) にすると、どれも「陽性」のグループに入らないので、感度は 0.0 (0%)、偽陽性率も 0.0 (0%)なので、原点に点が打たれます。逆に閾値を 0.0 (というか -∞) にすると、全て「陽性」のグループに入るので、感度は 1.0 (100%)、偽陽性率も 1.0 (100%) なのでグラフ最右上に点が打たれます。
閾値を 0.5 と決めると、感度が 0.6 (60%)、偽陽性率が 0.1 (10%) だったとしましょう。そうすると、(0.6, 0.1) のところに点が打たれます (下の図に赤い点で示しました) 。閾値を下げて 0.4 にしたら感度が 0.85 (85%)、偽陽性率が 0.4 (40%) だったとしましょう。図の水色の点になります。
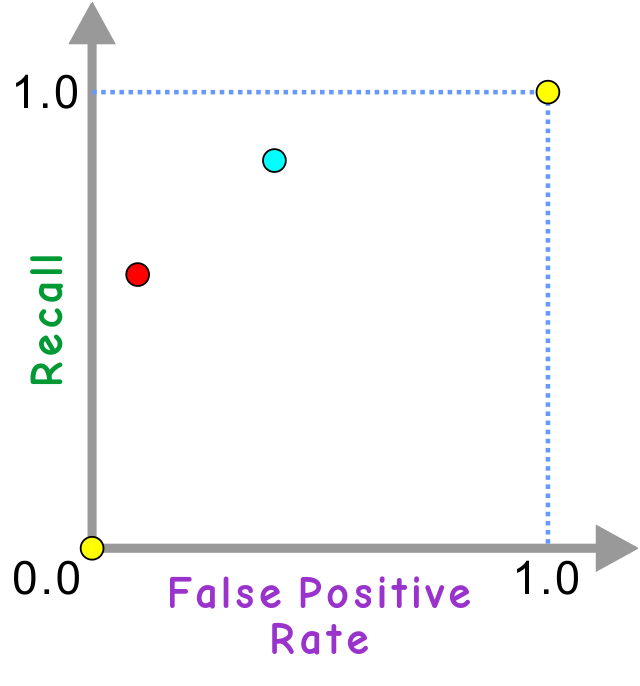
このように、閾値を変えていくと原点と (1.0, 1.0) の間に点が打たれて行きます (閾値自体はグラフ上には現れないのがポイント)。サンプル数が少ないとこれらの点を結んでもかくかくした線にしかなりませんが、サンプル数が十分多ければ、なめらかな曲線になっていきます。
これが ROC曲線です。
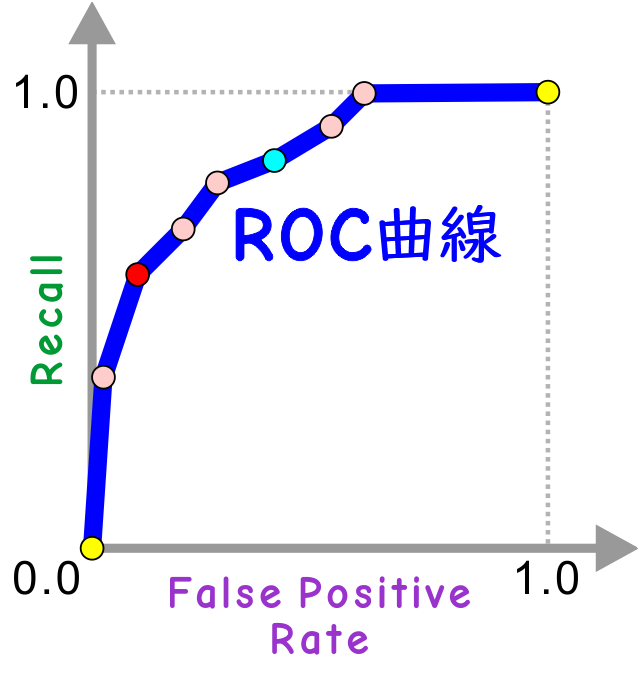
なお、似たような概念の曲線として PR曲線というものもあります。これは Precision-Recall Curve のことで、ROC曲線と同様のことを、適合度 (precision) と感度 (recall) を軸としたグラフとしてプロットします。
「使える」判定とは、ある閾値に対してなるべくすっぱり「疾患あり/なし」のグループ分けができるものでした。言い換えると、偽陽性率をなるべく上げずに感度を上げられるもの、です。ROC曲線上では、感度が高く、偽陽性率が低い状態は、左上のほうの点で表されます。すなわち、ROC曲線が左上に寄っているほど「良い判定」ということになります。
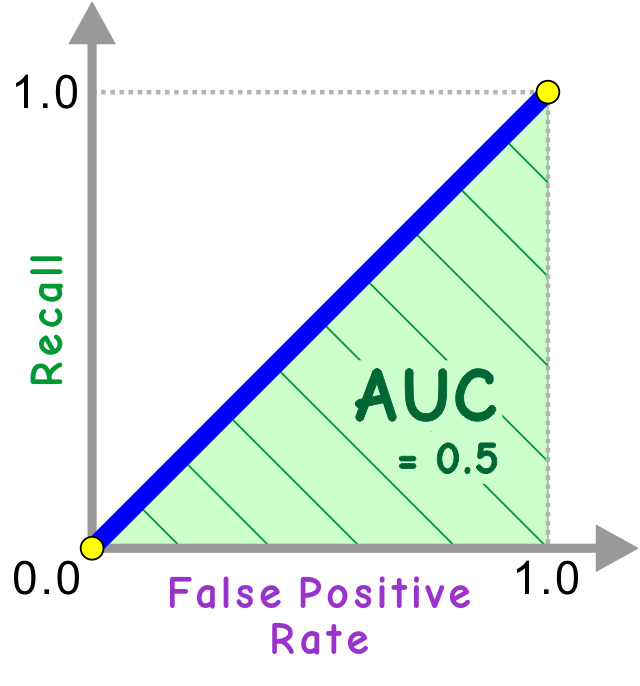
逆に「使えない」判定だった場合はどうなるでしょう? たとえば極端な例としてサイコロをいくつか振って出力値を決めた、としましょう。その場合は、閾値をどう決めても、分けた二つのグループにはどちらも同じ割合で「疾患あり/なし」が入ります。そうすると、感度が上がると、同じだけ偽陽性率が上がります。ROC曲線は、原点 (0.0, 0.0) から右上 (1.0, 1.0) へ向かう直線となります。
えっ、それよりも曲線が下に行く場合、ですか? それは陽性と陰性を逆にしたほうがマシということで… (「100%外れる占い」は役に立つのです :-)。
「ROC曲線が左上に寄っているほど『良い判定』」ということならば、今度はそれを数値化したくなるのが人情です。やりかたはいろいろ考えられて、なんなら、ROC曲線上の点と左上の (0.0, 1.0) の点との間の距離の最小値を見るとかでもよいわけですが、もっと単純で見た目でも解りやすいのが AUC です。
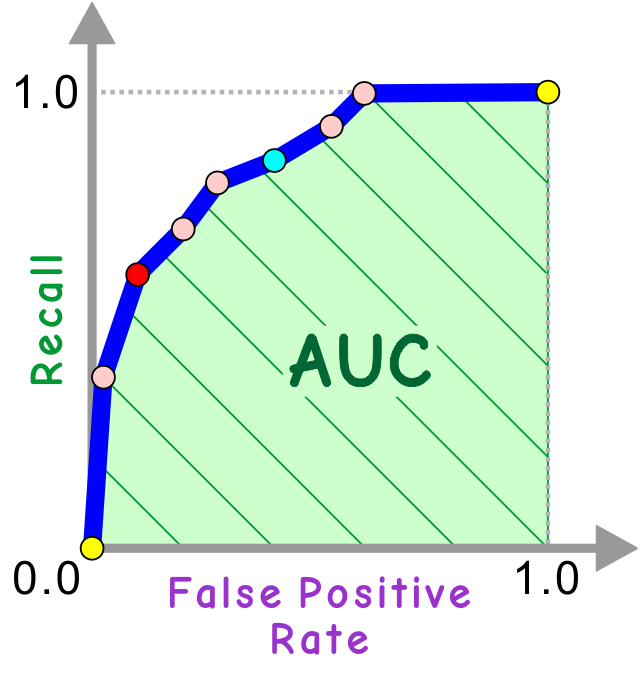
AUC とは Area Under Curve (曲線の下の面積) のことで、縦横 0.0〜1.0 の間のROC曲線の下にある領域の面積を指します (気持ちとしては「縦横 0.0〜1.0 の全体に対する面積の割合」ですが「全体の面積」は 1.0 なので同じことです)。なので、最大値は 1.0 です。完璧な判定ならば感度 1.0 偽陽性率 0.0 にできる、ということですね。面積という意味での最小値は 0.0 ですが、サイコロを振るのと変わらないランダムな判定の場合は「原点 (0.0, 0.0) から右上 (1.0, 1.0) へ向かう直線」なので、“最悪” を表す値が 0.5 になります。
ちなみに PR曲線に対する AUC というものももちろん考えられますし、使われることもあります (その場合の最悪値は 0.5 ではありません)。ROC曲線に対するものと明確に区別したい場合は “ROC AUC”、”PR AUC” という言い方をしたりします (微妙に長い)。単に AUC と言った場合は ROC曲線に対するものを指すことが多いように思われますが、念の為、注意が必要です。
AUC によってとりあえず複数の判定方法の良し悪しを較べることはできます。ですが、0.60 と 0.61 でどれくらい違うか、とか、その違いは 0.70 と 0.71 の違いと同程度なのか、とかは簡単には言えません。
これもあくまで指標の一つ、ということを忘れずに理解し活用するとよいと思います。




