技術研究所の(あ)です。
今、機械学習がものすごく活用されている対象といえば、自然言語か画像です。医用画像から機械学習で疾患の分類を行ったりする研究は我々技術研究所でも行っており、最近も「円錐角膜が進行性か否かを前眼部OCTの画像から推測する」事に関する共同研究の論文や、「角膜感染症の種類を光学写真から見分ける」事に関する共同研究の論文などが学術誌に掲載されました。
画像の分類などの性能の評価指標には 感度や特異度、F値、ROC曲線とAUC などがあります。今回のタイトルの「感度とF値」もこれらの一部ですね。
が、しかし、この「感度とF値」という言葉の組み合わせ、他の文脈でも出てきます。その文脈とはカメラの世界。感度は撮像素子 (やフィルム) に関する数値、F値はレンズに関する数値です。
画像分類などを行うには「(よい) 画像をどう撮るか」の話は欠かせません。すなわち、これらカメラの話も画像分類をやるのに無縁な話ではありません。ということで、今回はカメラのほうの感度とF値の話です。

まずは「感度」の話から。感度とは「どれくらい弱い光まで捉えられるか」の指標です。
光は波としての性質も持っていますが、粒 (光子) としても数えられ、光の強さとは粒の数の多さでもあります。光を受け止めて電気信号に変換するのが撮像素子ですが、ある程度の数の光子を受け止めるごとに電荷が (電子として) 溜まってゆき一定時間の間にどれだけの数の光子を受け止めたか、が電子の量として記録され、それが電圧などに変換されて出力されます。
このとき、ちょっとでも電荷が溜まっていれば「光が来た!」として反応し出力するようにすれば、感度は高くなります。しかし残念ながら、この世には撮像素子が受け止めて電荷に変換してしまう、「受けたい光」以外のノイズ、外からくるものや、そもそも光を受けていない状態でも撮像素子をちょこっとだけ流れてしまう電流 (暗電流) などがあります (電荷を読み出すときに紛れ込むノイズもあります)。なので、ちょっとの電荷で「来た!」と反応すると、それは単にノイズだったりする可能性が高くなってしまいます。
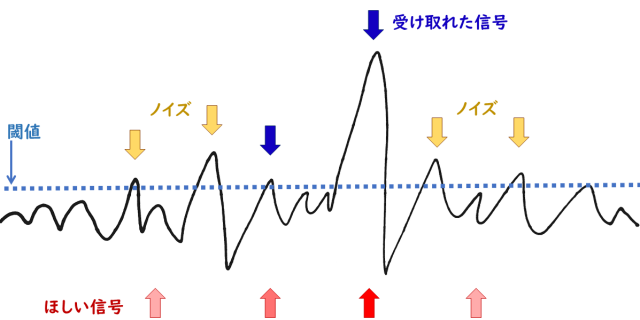
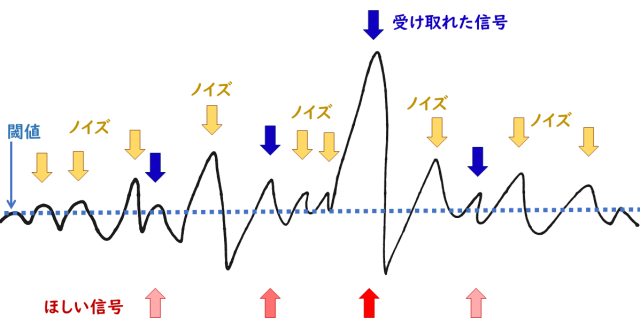
ある程度の電荷の量まではノイズだろうとみなして切り捨てるのがノイズ対策として真っ先に思いつきますが、それは同時に感度を犠牲にすることを意味します。このあたりは、陽性/陰性の性能評価で出てくる「感度」と同じで、ROC曲線の由来であるレーダーの話とほぼそのまま対応します。
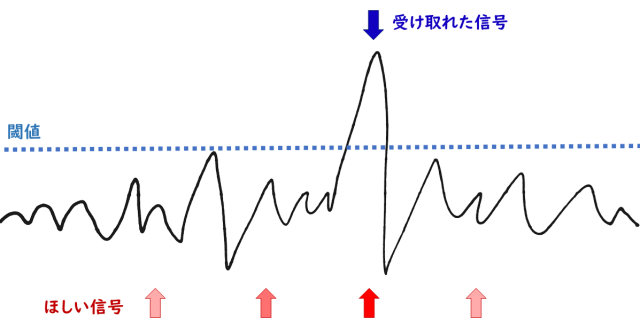
ノイズに負けずに感度を高くするにはどうすればよいでしょう? 方向性はまず大きく二つ考えられます。
- ノイズを減らす
- 撮像素子に、被写体からの光がより沢山届くようにする
1 のノイズを減らすのにとても有効な方法としては「撮像素子の温度を下げる」というのがあります。暗電流は素子の温度を下げることで減らすことができ、温度が下がると熱によるノイズも減ります。天体撮影などの用途でペルチェ素子で冷やす冷却CCD/冷却CMOSカメラが売られていますし、本格的な天文観測などだと液体窒素冷却CCDカメラなんていうのも使われます。
2 の撮像素子が光を多く受け取るためには、
- 素子が光を受ける時間を増やす
- 素子が光を受ける面積を増やす
- より広い範囲から素子に光を集める
の 3つの方策が考えられますが、a. 時間を増やすとその分、ノイズも増えてしまうので、これはいまいちです。b. は、ひとつひとつの撮像素子の面積を増やすと、同じ面積に入れられる撮像素子の数が減るので、解像度 (画素数) が犠牲になります。同じサイズのセンサを搭載したデジタルカメラでも、一般的に画素数が少ないもののほうがより高感度まで設定できるようになっています。
そして c. ですが、これは撮像素子側というより、そこに光を集めて届けるレンズ (やミラー) 側の話になります。
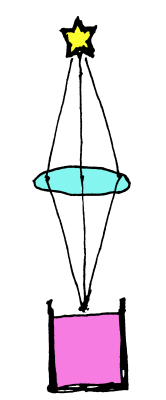
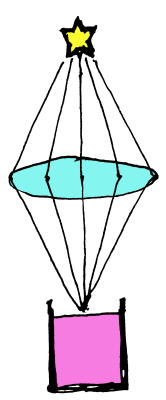
レンズと言うと、虫眼鏡のイメージで拡大した像を得るの (だけ) が目的と思っている方もいるかもしれません。しかし、レンズにはもう一つ、「同じところから出た光を一点にかき集める」という重要な役割があります。
すばる望遠鏡など、大きな天体望遠鏡では、レンズの代わりにミラーを使って、何m×何m もの広い範囲に届いた同じ天体の光を小さな (いや、一般のデジタルカメラよりは大きいと思いますが)
撮像素子に集めます。一般のカメラのレンズも同様で、レンズ前面の各所から入った、同じところから来た光を小さな撮像素子に集めます。
そうすると、単純に考えてレンズ前面の面積が大きいほど光をたくさん集められます。レンズ内の「絞り」で取り込んだ光の一部のみを撮像素子に送ることはできますが、レンズで集めた以上の光は届けられません。
一方、撮像素子には面積があるので、この面積が被写体側のどれくらいの広さに相当するか、すなわち、一つの撮像素子でどれくらいの広さからの光を受けるかも考えねばなりません。
ズームレンズ付きのカメラで遠くのものを大きく写そうとするとズーム(イン)して「望遠」側に寄せます。遠くのものを大きく写す、ということは、見た目の角度 (視野角) としては小さいものを大きく写すことになります。そして視野角が小さい、ということは、そこから出て、レンズに届く光も少ない、ということになります。望遠側に寄せる、というのは、レンズとしては「焦点距離」が長くなっていることに相当します。
というわけで、これらをまとめると、一つの撮像素子が受け取れる光は、焦点距離が長いほど少なくなります。具体的には、「面積」なので、焦点距離の二乗に反比例して少なく(暗く)なります。
レンズの前面の、(実質的に撮像素子に届く) 光を取り入れられる部分の直径をそのレンズの有効径あるいは有効口径 (Effective Aperture) と呼び、D で表します (diameter の ‘d’ ですかねぇ)。そしてレンズの焦点距離は f (focal length の ‘f’ ですね) で表します。
一つの撮像素子に集められる光の量は、光を取り入れる側の「面積」に比例して多くなるので、D^2 に比例し、そして焦点距離の二乗、f^2 に反比例します。なので、
F = f/D
と定義すると、光の量は F^2 に反比例することになり、この F の値を「F値」(F-number) と呼びます (ちなみに陽性/陰性の性能評価で出てくるほうの「F値」は “F-measure” です)。’F’ を使うのは、焦点距離と同じく “focal” 由来のようです (大文字と小文字で区別します)。F値が小さいほど、たくさんの光が集められるので、F値を小さくできるレンズほど「明るい」レンズということになります。F2.0 のレンズとか、F5.6 のレンズのような感じで表現します。
さてこの F値の定義、
「なぜ D/f じゃないの?」「f^2/D^2 のほうがシンプルなんじゃない?」
という疑問が湧くわけですが、今のところきちんとは調べきれていません。おそらく、通常出てくる値の範囲が扱いやすいから、というような理由ではないかなぁ、と予想します。
F0.5なんていうものすごく明るいレンズも存在はしますが、F1より小さいレンズはそうそう見かけません。明るくないレンズだと F5 とか F6 くらいのところでしょうか。絞りを絞って F11 とかで撮影することもよくあります。これが、F値を D/f で定義すると、全て逆数になりますから、1 はそのままですが、5 は 0.2 に、6 は 0.17 に、11 は 0.09 になります。なんか細かいですよね。
そして、F値を二乗で定義すると、これも 1 はそのままですが、5 は 25 に、11 は 121 になって、ちょっと絞るとがんがん値が大きくなります。慣れの要素も強いとは思いますが、F= f/D でまあよいのかな、という気がします。
なお、感度のほうで使われる数値 (ISO感度) は、フィルムカメラのころは 100〜3200 くらいが普通出てくる範囲 (数字が大きいほうが感度が高い) だったと思うのですが、デジタルカメラの進歩にともない 51200 とかの値も普通に出てくるようになって、ちょっとインフレ気味な感じです^^;。
感度は、上げようとするとノイズなどとの戦いになりますが、F値のほうは、小さくすると焦点の合う範囲 (被写界深度) が狭くなる、というトレードオフがあります。これらに撮像する時間 (シャッタースピード) (長いほど光を多く捉えられるが、ノイズ以外に動くものがブレるというトレードオフがある) を加えた三要素をどう調整するかがカメラによる撮影においては重要になります。
それぞれの要素の意味合いを理解して、用途や目的に応じて設定できるようにしてゆきましょう。




